- 19 Tháng tám 2018
- 2,749
- 6,038
- 596
- 25
- Thái Bình
- Đại học Y Dược Thái Bình
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 Helu các ban, các bạn ôn thi đến đâu rồi, các bạn đã học sang chương 2 chưa
Helu các ban, các bạn ôn thi đến đâu rồi, các bạn đã học sang chương 2 chưa BÀI 1 - LŨY THỪA - HÀM SỐ LŨY THỪA
I. Khái niệm lũy thừa
1. Lũy thừa với số mũ nguyên
Chọn $n$ là một số nguyên dương. Với $a$ là một số thực tùy ý, lũy thừa bậc $n$ của $a$ là tích của $n$ thừa số $a$
$a^n=a\cdot a\dotsm a$ (có $n$ thừa số $a$)
Với $a \neq 0$ ta có : $a^0=1;a^{-n}=\dfrac1{a^n}$
2. Căn bậc n
Cho số thực $b$ và số nguyên dương $n\, (n\geq 2)$. Số $a$ được gọi là căn bậc $n$ của số $b$ nếu $a^n=b$
3. Phương trình $x^n=b$
a. Kết quả biện luận nghiệm của phương trình $x^n=b$
- Trường hợp $n$ lẻ và $b\in \mathbb{R}:$ Với mọi số thực $b$, phương trình có nghiệm duy nhất là $x=\sqrt[n]{b}$
- Trường hợp $n$ chẵn:
+ Với $b<0$, phương trình vô nghiệm
+ Với $b=0$, phương trình có một nghiệm $x=0$
+ Với $b>0$, phương trình có hai nghiệm đối nhau là $x_{1}=\sqrt[n]{b};x_{2}=-\sqrt[n]{b}$
b. Tính chất của căn bậc $n$
+ $\sqrt[n]{a}\cdot \sqrt[n]{b}=\sqrt[n]{ab};\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}$
+ $\left ( \sqrt[n]{a} \right )^{m}=\sqrt[n]{a^{m}};\sqrt[n]{a^{n}}=\left\{ \begin{array}{l} a,\textrm{khi n lẻ} \\ \left | a \right |,\textrm{khi n chẵn} \end{array} \right.$
+ $\sqrt[n]{\sqrt[k]{a}}=\sqrt[nk]{a}$
4. Lũy thừa với số mũ hữu tỷ
Cho $a$ là số thực dương và số mũ hữu tỷ $r=\dfrac mn$, trong đó $m\in \mathbb{Z},n\in \mathbb{N},n\geq 2$. Lũy thừa $a$ với số mũ $r$ là số $a^r$ được xác định bởi: $$a^{r}=a^{\dfrac{m}{n}}=\sqrt[n]{a^{m}}$$
5. Lũy thừa với số mũ vô tỉ
Ta gọi giới hạn của dãy số $\left ( a^{r_{n}} \right )$ là lũy thừa của $a$ với số mũ $\alpha $, khí hiệu là $a^{\alpha }$ $$a^{\alpha }=\lim\limits_{n \to +\infty} a^{r_{n}} \quad \text{với} \quad \alpha =\lim\limits_{n \to +\infty} r_{n}$$
6. Tính chất của lũy thừa với số mũ thực
Cho $a,b$ là những số thực dương; $m,n$ là những số thực tùy ý. Khi đó:
$a^{m}\cdot a^{n}=a^{m+n};\dfrac{a^{m}}{a^{n}}=a^{m-n};\left ( a^{m} \right )^{n}=a^{mn};\left ( ab \right )^m=a^{m}\cdot b^{m};\left ( \dfrac{a}{b} \right )^{m}=\dfrac{a^{m}}{b^{m}}$
Nếu $a>1$ thì $a^{m}> a^{n}\Leftrightarrow m> n$
Nếu $a<1$thì $a^{m}> a^{n}\Leftrightarrow m< n$
Ghi nhớ
1. Căn bậc $1$ của $a$ là $a$
2. Căn bậc $n$ của $0$ là $0$ với mọi $n$ nguyên dương
3. Số âm không có căn bậc chẵn
4. Với $n$ là số nguyên dương lẻ, ta có: $\sqrt[n]{a}> 0\Leftrightarrow a> 0\quad \textrm{và}\quad \sqrt[n]{a}< 0\Leftrightarrow a< 0$
5. $\sqrt[n]{a^{n}}=a$ nếu $n$ lẻ; $\sqrt[n]{a^{n}}=\left | a \right |$ nếu $n$ chẵn
II. Hàm số lũy thừa
a. Khái niệm: Hàm số $y=x^{\alpha }$ với $\alpha \in \mathbb{R}$ được gọi là hàm số lũy thừa
b. Đạo hàm: $\left ( x^{\alpha } \right )'=\alpha \cdot x^{\alpha -1}$
c. Tập xác định
Hàm số lũy thừa $y=x^{\alpha}$ với $\alpha \in \mathbb{R}$
+ Nếu $\alpha$ nguyên dương $\Rightarrow$ TXĐ: $\mathrm{D}=\mathbb{R}$
+ Nếu $\alpha$ nguyên âm hoặc bằng $0 \Rightarrow$ TXĐ: $\mathrm{D}=\mathbb{R}\setminus \left \{ 0 \right \}$
+ Nếu $\alpha$ không nguyên $\Rightarrow$ TXĐ: $\mathrm{D}=(0;+\infty)$
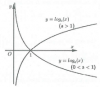
d. Đồ thị
Xét trên khoảng $\left ( 0;+\infty \right )$ thì đồ thị của hàm số lũy thừa $y=x^{\alpha }$ luôn đi qua điểm $(1;1)$
Hình dưới là đồ thị của hàm số lũy thừa trên $\left ( 0;+\infty \right )$ ứng với các giá trị khác nhau của $\alpha$
e. Bảng tóm tắt tính chất của hàm số lũy thừa $y=x^{\alpha }$ trên khoảng $\left ( 0;+\infty \right )$
| $a>0$ | $a<0$ | |
| Đạo hàm | $y'=\alpha \cdot x^{\alpha -1}$ | $y'=\alpha \cdot x^{\alpha -1}$ |
| Chiều biến thiên | Hàm số luôn đồng biến | Hàm số luôn nghịch biến |
| Tiệm cận | Không có | Tiệm cận ngang là trục $Ox$, tiệm cận đứng là trục $Oy$ |
| Đồ thị | Đồ thị hàm số luôn đi qua điểm $(1;1)$ | Đồ thị hàm số luôn đi qua điểm $(1;1)$ |
Xem thêm:
[Ôn thi THPTQG] Hàm số và ứng dụng của đạo hàm
[Khảo sát] Tâm tư nguyện vọng của thành viên
[Khảo sát] Ôn thi học kì cùng box Toán
[Chia sẻ] Cảm nang trình bày lời giải một bài toán
Ôn thi HSG Toán THCS