[Chuyên đề 1 ] Lượng giác

[letrang3003]

Hàng khủng

 

[tell_me_goobye]

1)
a) cho ABC CM:

[TEX] \sum tan^6 \frac{A}{2} \geq \frac{1}{9} [/TEX]
b) CMR

[TEX] tan a+tan b+tan c -\frac{sin(a+b+c)}{cosacosbcosc} =tan a.tan b.tan c[/TEX]

 

[letrang3003]

1)

b) CMR

[TEX] tan a+tan b+tan c -\frac{sin(a+b+c)}{cosacosbcosc} =tan a.tan b.tan c[/TEX]

Điều phải chứng minh

 

[duynhan1]

1)
a) cho ABC CM:
[TEX] \sum tan^6 \frac{A}{2} \geq \frac{1}{9} [/TEX]

Áp dụng BDT :
[TEX]\huge \sum tan {\frac{A}{2}} \ge \sqrt{3}[/TEX]

AM-GM:
[TEX]\Large tan^6 {\frac{A}{2}} + \frac{5}{27} \ge \frac{6 tan {\frac{A}{2}}}{3\sqrt{3}} =\frac{2 tan {\frac{A}{2}}}{sqrt{3}} [/TEX]

[TEX]\Rightarrow \sum tan^6 {\frac{A}{2}} \ge \frac{2 \sum tan{\frac{A}{2}} }{\sqrt{3}} - \frac{15}{27} = \frac19 [/TEX]

 

[duynhana1]

[TEX]\forall x,y,z \in R^+[/TEX] và [TEX]\Delta ABC [/TEX] ta có :

[TEX]\Huge \sum {\frac{cosA}{x}} \le \frac{\sum x^2}{2xyz}[/TEX]

 

[minhkhac_94]

[TEX]\forall x,y,z \in R^+[/TEX] và [TEX]\Delta ABC [/TEX] ta có :

[TEX]\Huge \sum {\frac{cosA}{x}} \le \frac{\sum x^2}{2xyz}[/TEX]

[TEX]<=> 2\sum{yzcosA} \le (x^2+y^2+z^2)[/TEX]
Chứng minh trên = véctơ
Đặt các véc tơ đơn vị lên các cạnh của tam giác
[TEX](x\vec{e_1}+y\vec{e_2}+z\vec{e_3})^2 \geq 0[/TEX]
<=>[TEX]<=> 2\sum{yzcosA} \le (x^2+y^2+z^2)[/TEX]

 

[letrang3003]

Giải phương trình :

 

[letrang3003]

Giải phương trình

 

[minhkhac_94]

Xét

vô nghiệm
Xét TH

khác -1

Cuối cùng là thử lại 2 ĐK

 

[minhkhac_94]

Giải phương trình :

Là pt đối xứng sin và cos
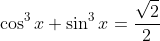
Đặt sinx+cosx=t
________________________________

 

[duynhan1]

Giải phương trình :

[TEX](sin x+ cos x)( 1 - sin x . cos x) = \frac{\sqrt{2}}{2}[/TEX]

[TEX]t = sin x + cos x \ \ (|t| \le \sqrt{2}) \Rightarrow t( 2 - (t^2-1) ) = \sqrt{2} [/TEX]

[TEX]\Leftrightarrow -t^3 + 3t - \sqrt{2} = 0 [/TEX]

[TEX]\Leftrightarrow ( t-\sqrt{2})(t^2 +\sqrt{2} t - 1) = 0 [/TEX]

 

[herrycuong_boy94]

Cho PT

thoả mãn

vowis mọi x1, x2 thoả mãn

chứng minh f(x) đồng nhất bằng 0

 

[duynhana1]

Cho PT

thoả mãn

vowis mọi x1, x2 thoả mãn

chứng minh f(x) đồng nhất bằng 0

Chú ý CT :
[TEX]a. sin \al + b .cos \al = \sqrt{a^2+b^2} sin (\al+arcsin(\frac{b}{ \sqrt{a^2+b^2}} ) [/TEX]

Nhưng cái đề cậu đánh sao sao ý

 

[letrang3003]

tìm m để phương trình có 8 nghiệm

)

Đề bài sai , PT kia đã có 1 nghiệm sin x=0 tức là x chỉ đc nhận 1 giá trị là 2\pi còn PT bậc 2 kia có tối đa 2 nghiệm t với t là sin x vậy x có thể có 4 giá trị trong (0,3\pi) nếu \sin x dương còn có 2 nghiệm trên (0,3\pi) nếu \sin x âm vậy không thể có 8 nghiệm được

 

[legendismine]

Chứng minh rằng nếu tam giác ABC thoả đk :
[tex]\frac {cosA.cosB}{cosC}+\frac {cosB.cosC}{cosA}+\frac {cosA.cosC}{cosB}=\frac {3}{2}[/tex]
thì tam giác ABC đều

 

[letrang3003]

Chứng minh rằng nếu tam giác ABC thoả đk :
[tex]\frac {cosA.cosB}{cosC}+\frac {cosB.cosC}{cosA}+\frac {cosA.cosC}{cosB}=\frac {3}{2}[/tex]
thì tam giác ABC đều

 

[letrang3003]

Ta sẽ cm bđt [TEX]\sin^2 x+\sin^2 y+\sin^2 (x+y)\le\frac{9}{4}\,\forall x,y\in\mathbb{R}\quad (1)[/TEX].
[TEX](1)\Leftrightarrow \cos 2x+\cos 2y+\cos 2(x+y)\ge -\frac{3}{2}[/TEX].
Xét các vector đơn vị [TEX]\vec{e_1},\vec{e_2},\vec{e_3}[/TEX] sao cho [TEX]\left(\vec{e_1},\vec{e_2}\right)=2x,\left(\vec{e_2}, \vec{e_3}\right)=2y \Rightarrow \left(\vec{e_1},\vec{e_3}\right)=2(x+y)[/TEX]. Ta có
[TEX]\left(\vec{e_1}+\vec{e_2}+\vec{e_3}\right)^2\ge 0[/TEX]
[TEX]\Leftrightarrow 3+2\left(\cos2x+\cos 2y+\cos 2(x+y)\right)\ge 0[/TEX]
[TEX]\Leftrightarrow \cos2x+\cos 2y+\cos 2(x+y)\ge -\frac{3}{2}[/TEX] (đpcm)

hay

 

[williamdunbar]

Cho tam giác ABC thỏa mãn điều kiện [tex] \frac{cos A.cos B}{cos C} +\frac{cos B.cos C}{cosA}+\frac{cos C.cos A}{cos B} =\frac{3}{2} [/tex].
CMR: tam giác ABC đều

 

[duynhana1]

Cho tam giác ABC thỏa mãn điều kiện [tex] \frac{cos A.cos B}{cos C} +\frac{cos B.cos C}{cosA}+\frac{cos C.cos A}{cos B} =\frac{3}{2} [/tex].
CMR: tam giác ABC đều

[TEX]\Leftrightarrow 2\sum cos^2A. cos^2B = 3.cosA.cosB.cosC [/TEX]

AM-GM và để ý : [TEX]cosA.cosB.cosC \le \frac18[/TEX]

 

[letrang3003]

minh xin post 1 bai lam quen vs dien dan nha
giai pt
tanx + tan2x +4cot4x = sin(x/2) + cos(x/2)

Sử dụng công thức này:

thì dễ dàng đưa về :

đã có nhân tử chung