B
bigbang195
Dạng bài hơi khó một chút
1.Cho a,b,c \geq 0. CMR
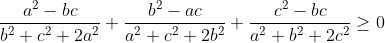
2.Cho a,b,c >0 . CMR :
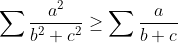
Bài 1:
[TEX]VT =\sum \frac{(a^2-bc)^2}{(a^2-bc)(b^2+c^2+2a^2)} \ge \frac{\sum a^2-\sum ab}{\sum (a^2-bc)(b^2+c^2+2a^2)}[/TEX]
Chỉ cần CM [TEX]\sum (a^2-bc)(b^2+c^2+2a^2) \ge 0[/TEX]
hay [TEX]2 \sum a^4+2\sum a^2b^2 \ge \sum a^3b +\sum b^3a+2 abc(a+b+c)[/TEX]
ta chỉ cần Sử dụng
[TEX]\left{ \sum a^4+\sum a^2b^2 \ge 2 \sum a^3b \\ \sum b^4+\sum b^2a^2 \ge 2\sum b^3a \\ \sum a^4+\sum a^2b^2 \ge 2abc(a+b+c)[/TEX]

