[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
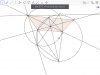
1. Từ A nằm ngoài (O), vẽ tiếp tuyến AM, AN và cát tuyến ACD. B thuộc cung CM không chưa D, H là giao điểm của MN và BD, E là giao của CH và (O).
a, Gọi K là giao điểm của AH và đường tròn ngoại tiếp ta, giác AMN. Chứng minh : AEKC và HKCD là tứ giác nội tiếp
b, Chứng minh: A,E,B thẳng hàng.
2. Người ta tô màu xanh hoặc đỏ tất các cạnh của 1 đa giác lồi biết tổng độ dài các cạnh màu xanh nhỏ hơn nửa chu vi đa giác và không có cạnh nào liền nhau được tô màu đỏ. Chứng minh rằng: không thể có đường tròn nào nội tiếp đa giác.
a, Gọi K là giao điểm của AH và đường tròn ngoại tiếp ta, giác AMN. Chứng minh : AEKC và HKCD là tứ giác nội tiếp
b, Chứng minh: A,E,B thẳng hàng.
2. Người ta tô màu xanh hoặc đỏ tất các cạnh của 1 đa giác lồi biết tổng độ dài các cạnh màu xanh nhỏ hơn nửa chu vi đa giác và không có cạnh nào liền nhau được tô màu đỏ. Chứng minh rằng: không thể có đường tròn nào nội tiếp đa giác.
