Z
z0987654321
cũng không hay đâu bạn ; cách hệ số bất định thì nai mò giỏi thì làm nhanh thôi màB tách hay lắm.Mà tại sao bạn cộng thêm 3 và -1 thế..
Chia sẻ m it kinh nghiệm với :|
cũng không hay đâu bạn ; cách hệ số bất định thì nai mò giỏi thì làm nhanh thôi màB tách hay lắm.Mà tại sao bạn cộng thêm 3 và -1 thế..
Chia sẻ m it kinh nghiệm với :|
$=(x^2+3x+2)9x+3x+12\\(x+1)(x+2)9x+3(x+4)
8. Phương pháp hệ số bất định như thế nào, biến đổi nó và dạng của nó ra sao? Bạn nào biết xin chỉ cho!Phân tích đa thức thành nhân tử là 1 kiến thức cơ bản của chương trình Toán lớp 8. Đây là dạng toán tương đối khó và khá phức tạp. Trong các kì thi HSG, thi chuyển cấp, thi chuyên Toán, ... đều có các bài toán về phân tích đa thức thành nhân tử. Vì vậy mình lập pic này để mọi người cùng nhau trao đổi kiến thức, nâng cao khả năng của mỗi người.
Mong các bạn tham gia tích cực và tuyệt đối không Spam
Một số phương pháp cơ bản về phân tích đa thức thành nhân tử
1. Phương pháp đặt nhân tử chung
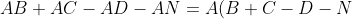)
2. Phương pháp dùng hằng đẳng thức
Vận dụng các hằng đẳng thức để biến đổi đa thức thành tích các nhân tử hoặc luỹ thừa của một đa thức đơn giản.
3. Phương pháp nhóm nhiều hạng tử
Dùng các tính chất giao hoán, kết hợp của phép cộng các đa thức, ta kếp hợp những hạng tử của đa thức thành từng nhóm thích hợp rồi dùng các phương pháp khác phân tích nhân tử theo từng nhóm rồi phân tích chung đối với các nhóm.
4. Phương pháp tách
Ta có thể tách 1 hạng tử nào đó của đa thức thành hai hay nhiều hạng tử thích hợp để làm xuất hiện những nhóm hạng tử mà ta có thể dùng các phương pháp khác để phân tích được
Ví dụ:
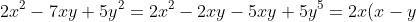-5y(x-y)=(x-y)(2x-5y))
5. Phương pháp thêm bớt cùng một hạng tử
Ta có thể thêm bớt 1 hạng tử nào đó của đa thức để làm xuất hiện những nhóm hạng tử mà ta có thể dùng các phương pháp khác để phân tích được.
Ví dụ:
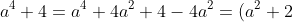^2-(2a)^2=(a^2+2-2a)(a^2+2+2a))
6. Phương pháp đặt biến phụ
Trong một số trường hợp, để việc phân tích đa thức thành nhân tử được thuận lợi, ta phải đặt biến phụ thích hợp.
Ví dụ: Phân tích thành nhân tử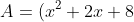^2+3x(x^2+2x+8)+2x^2)
Đặtta có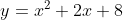
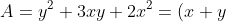(2x+y) \\ \Rightarrow A=(x^2+3x+8)(x+2)(x+4))
7. Phương pháp giảm dần số mũ của lũy thừa
Phương pháp này chỉ áp dụng được cho các đa thức nhưlà những đa thức có dạng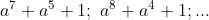 . Khi phân tích các đa thức có dạng như trên thì biểu thức sau khi phân tích đều có 1 nhân tử là
. Khi phân tích các đa thức có dạng như trên thì biểu thức sau khi phân tích đều có 1 nhân tử là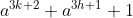
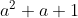
Ví dụ: Phân tích đa thức thành nhân tử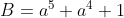
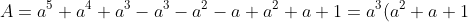-a(a^2+a+1)+(a^2+a+1)=(a^2+a+1)(a^3-a+1))
8. Phương pháp hệ số bất định (nói sau)
Khi phân tích đa thức thành nhân tử phải biết vận dụng linh hoạt nhiều phương pháp và phối hợp 1 cách hợp lí
giup mình với
x^5+x^4+1
các bạn giải dùm mình bài này với :
x(x+1)(x+2)(x+3) + 1

