[Toán 7]Rung chuông vàng

[daovuquang]

Bài này dễ quá.
Cộng 3 vế trên, ta có:
2(x+y+z)=0
\Rightarrow x+y+z=0
\Rightarrow đpcm.

 

[nuhoangachau]

Câu 11:
Cho 3 số a, b, c thỏa mãn a.b.c = 1. Tính:

 

[daovuquang]

Không có ai làm đành làm vậy.
[TEX]S=\frac{1}{1+a+ab}+\frac{1}{1+b+bc}+\frac{1}{1+c+ca}[/TEX]
[TEX]=\frac{abc}{abc+a+ab}+\frac{1}{1+b+bc}+\frac{abc}{abc+abc^2+ca}[/TEX]
[TEX]=\frac{bc}{1+b+bc}+\frac{1}{1+b+bc}+\frac{b}{1+b+bc}[/TEX]
[TEX]=1[/TEX]

 

[nuhoangachau]

Bài 12:
Cho

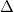ABC cân tại A. Kẽ BH

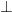AC. Gọi D là một điểm thuộc cạnh BC. Kẽ DE

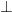AC, kẽ DF

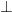AB. Ch/m: BH = DE + DF

 

[luuquangthuan]

Bài 12:
Cho

ABC cân tại A. Kẽ BH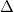

AC. Gọi D là một điểm thuộc cạnh BC. Kẽ DE

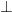AC, kẽ DF

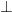AB. Ch/m: BH = DE + DF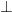

Kẻ DO vuông góc với BH ta có DO // AC
BH // DC ( cùng vuông góc với AC)
\Rightarrow DC = OH theo tính chất đoạn chắn //. (1)
Xét tam giác BFD và tam giác DOB ta có:
O = F = 90 độ
Chung BD
FBD = ODB ( cùng bằng ACB )
\Rightarrow tam giác BFD = tam giác DOB
\RightarrowOB = DF (2)
Từ (1) và (2) ta có
DE + DF = OB + HO = BH
\Rightarrowđpcm
Nhớ thanks nghen bạn - vấn đề này thì đừng quên nhé

Chú ý mem ko được dùng chữ đỏ.
Ps: Đã sửa!

 

[nuhoangachau]

Kẻ DO vuông góc với BH ta có DO // AC
BH // DC ( cùng vuông góc với AC)
\Rightarrow DC = OH theo tính chất đoạn chắn //. (1)
Xét tam giác BFD và tam giác DOB ta có:
O = F = 90 độ
Chung BD
FBD = ODB ( cùng bằng ACB )
\Rightarrow tam giác BFD = tam giác DOB
\RightarrowOB = DF (2)
Từ (1) và (2) ta có
DE + DF = OB + HO = BH
\Rightarrowđpcm

Cái màu hồng ý lớp 7 chưa học thì phải tính chất ý lên lớp 8 mới học thì phải
Cái này không thể chấp nhận được làm cái khác đi nhé>->-|-)|-)

 

[luuquangthuan]

Cái in đỏ ý lớp 7 chưa học thì phải tính chất ý lên lớp 8 mới học thì phải
Cái này không thể chấp nhận được làm cái khác đi nhé>->-|-)|-)

Bạn ơi! Thế là bạn chưa biết rồi!
Tính chất này trong chương trình lớp 7 không có! Nhưng trong chương trình nâng cao lại có thể sử dụng được. Vì vậy bài giải của tui là hoàn toàn đúng.
Nếu bạn thấy cách giải đó của tui khó hiểu thì tui sẽ giải cách khác:
CM tứ giác OHED là hình chữ nhật vì OH vuông góc HE
DE vuông góc HE
DO vuông góc OH
EH vuông góc OH
Như vậy tôi vẫn chứng minh được OH = DE

 

[nuhoangachau]

Bài 13:
Cho hai

vuông cân ABC và DBC. Hai đỉnh góc vuông A, D ở hai mặt phẳng khác nhau bờ BC. Cạnh huyền BC = 1. Người ta lấy các điểm M, N, P, Q lần lượt trên các cạnh AB, BD, DC, CA. Chứng minh rằng chu vi của hình bốn cạnh MNPQ không nhỏ hơn 2

 

[luuquangthuan]

Bài 13:
Cho hai

vuông cân ABC và DBC. Hai đỉnh góc vuông A, D ở hai mặt phẳng khác nhau bờ BC. Cạnh huyền BC = 1. Người ta lấy các điểm M, N, P, Q lần lượt trên các cạnh AB, BD, DC, CA. Chứng minh rằng chu vi của hình bốn cạnh MNPQ không nhỏ hơn 2

Để mình giải bài này cho nhé bạn.
Ta có ABCD là hình vuông ( cái này các bạn tự chứng minh , dễ lắm)
Áp dụng Py-ta-go ta có:
[TEX]AM^2[/TEX] + [TEX]AQ^2[/TEX] = [TEX]MQ^2[/TEX]
[TEX]BM^2[/TEX] + [TEX]BN^2[/TEX] = [TEX]MN^2[/TEX]
[TEX]DN^2[/TEX] + [TEX]DP^2[/TEX] = [TEX]NP^2[/TEX]
[TEX]CP^2[/TEX] + [TEX]CQ^2[/TEX] = [TEX]QP^2[/TEX]

Lại có [TEX]AM^2[/TEX] + [TEX]BM^2[/TEX] < CB = 1
Tương tự các cạnh BN, DN, DP, PC, CQ, AQ tự chứng minh.

\Rightarrow tổng bình phương bốn cạnh tứ giác MNPQ > 4
\Rightarrow đpcm

Chú ý mem ko được dùng chữ đỏ.
Ps: Đã sửa!

 

[luuquangthuan]

Bạn đừng spam nhé bạn!
Tui làm như thế được rùi!
Bạn chỉ ra sai chỗ nào? Tại sao sai!

 

[nuhoangachau]

Để mình giải bài này cho nhé bạn.
Ta có ABCD là hình vuông ( cái này các bạn tự chứng minh , dễ lắm)
Áp dụng Py-ta-go ta có:
[TEX]AM^2[/TEX] + [TEX]AQ^2[/TEX] = [TEX]MQ^2[/TEX]
[TEX]BM^2[/TEX] + [TEX]BN^2[/TEX] = [TEX]MN^2[/TEX]
[TEX]DN^2[/TEX] + [TEX]DP^2[/TEX] = [TEX]NP^2[/TEX]
[TEX]CP^2[/TEX] + [TEX]CQ^2[/TEX] = [TEX]QP^2[/TEX]

Lại có [TEX]AM^2[/TEX] + [TEX]BM^2[/TEX] < CB = 1
Tương tự các cạnh BN, DN, DP, PC, CQ, AQ tự chứng minh.
\Rightarrow tổng bình phương bốn cạnh tứ giác MNPQ > 4
\Rightarrow đpcm

Tất cả đều sai cả kết quả cũng sai tất có cần tui giải ra không hả bạn |-)|-)|-)

 

[nuhoangachau]

Bài 13:
Cho hai

vuông cân ABC và DBC. Hai đỉnh góc vuông A, D ở hai mặt phẳng khác nhau bờ BC. Cạnh huyền BC = 1. Người ta lấy các điểm M, N, P, Q lần lượt trên các cạnh AB, BD, DC, CA. Chứng minh rằng chu vi của hình bốn cạnh MNPQ không nhỏ hơn 2

Gọi O là giao điểm của BC và AD
Ta dễ dàng chứng minh được BC

AD (dễ lắm) và OA = OB = OC = OD =

Gọi I, K, L, T lần lượt là giao điểm của MQ với AD, MN với BC, NP với AD, PQ với BC.
Từ M hạ MI'

OA ; MK'

OB. Khi đó

MI'K vuông cân tại nên MI' = AI' và theo tính chất đoạn chắn song song ta có MK' = I'O
Ta luôn có: MI

MI'; MK

MK'
Nên:

Tương tự ta có:

Cộng từng vế các bất đẳng thức trên ta có:

(đpcm)

 

[quynhnhung81]

Ế ẩm quá
Cho một bài thì học sinh giỏi lớp 6 của trường mik nè

Chứng minh rằng tồn tại số tự nhiên k sao cho [TEX]3^k[/TEX] có ba chữ số tận cùng là 001

 

[luckybaby_98]

Ế ẩm quá
Cho một bài thì học sinh giỏi lớp 6 của trường mik nè

Chứng minh rằng tồn tại số tự nhiên k sao cho [TEX]3^k[/TEX] có ba chữ số tận cùng là 001

Bài này em thấy cũng dễ chị à..^^
Chắc năm nay lên lớp 8 em mí cảm thấy dễ....

Chứng minh rằng tồn tại số tự nhiên k sao cho [TEX]3^k[/TEX] có ba chữ số tận cùng là 001.

Áp dụng tính chất sự chia hết ta thấy:

Trong phép chia cho 1000 thì có 1000 nghìn số dư thuộc tập hợp {0,1,2,3....,999}
Theo đề bai ta xét số 1001 có các số: 3,[TEX]3^2, 3^3,....,3^1001[/TEX]
Nếu tồn tại 2 số có cùng số dư trong phép chia cho 1000, ta có giải sử sau:

Giả sử 2 số đó là [TEX]3^m , 3^n[/TEX] với điều kiện 0\leqn\leqm\leq1000
\Rightarrow [TEX]3^m - 3^n[/TEX] chia hết cho 1000
\Leftrightarrow[TEX]3^n.(3^m-n)[/TEX] chia hết cho 1000.

Vì bội chung nhỏ nhất của [TEX]3^n , 1000 [/TEX]=1
[TEX]3^m-n[/TEX] - 1 chia hết cho 1000.

Hay [TEX]3^m-n[/TEX] có tận cùng là 001 (đpcm)

Các " tình iu " ơi đừng nhìn nhầm nhé.....là 3^m-n đóa hông phải là [TEX]3^m[/TEX] - n đâu...)))

 

[nuhoangachau]

Bài 15:
Cho

ABC, AB = BC và

. Ta lấy một điểm I ở trong

ấy sao cho

;

. Tính

 

[harrypham]

Chào mọi người.
Trước đây topic này là nơi các bạn giao lưu học hỏi về các bài toán lớp 7.
Bây giờ topic này cũng sẽ như vậy.
Tuy nhiên để phù hợp với trình độ lớp 7hiện giờ (bây giờ là học kì I lớp 7), nên đề nghị các bạn tránh ra các bài toán có dính líu đến học kì II.
Bài toán phải đánh số thứ tự (bài 15 có bạn nào giải được không ).

Bài 16. Tìm [TEX]x[/TEX] biết

[TEX]2|5x-3|-2x=14[/TEX]​

Topic xin nói lại và chỉnh sửa thêm một số quy định
+ Gõ LaTeX
+ Gõ tiếng Việt có dấu
+ Lời giải đưa ra phải rõ ràng, không quá vắn tắt.
+ Không spam, nói tục, chửi bậy

Quy định về việc ra bài và giải bài:

+ Ra bài khó được công nhận : 2 thanks
+ Giải một bài khó : 5 thanks

 

[braga]

[TEX]2\left | 5x-3 \right |-2x=14[/TEX]
[TEX]\Leftrightarrow 2\left |5x-3 \right |=14+2x[/TEX]
[TEX]\Leftrightarrow \left |5x-3 \right |=\frac{14+2x}{2}[/TEX]
[TEX]\Leftrightarrow \left |5x-3 \right |=7+x[/TEX]
- Xét [TEX]x\geq \frac{3}{5}\Leftrightarrow 5x-3 \geq 0 \Leftrightarrow \left | 5x-3 \right |=5x-3[/TEX]
[TEX]5x-3=7+x \Leftrightarrow 4x=10\Leftrightarrow x=\frac{5}{2}[/TEX] ( thoả mãn điều kiện [TEX]x\geq\frac{3}{5}[/TEX] )
- Xét [TEX]x< \frac{3}{5}\Leftrightarrow 5x-3< 0\Leftrightarrow \left | 5x-3 \right |=-(5x-3)[/TEX]
[TEX] -(5x-3)=7+x \Leftrightarrow -6x=4\Leftrightarrow x=\frac{-2}{3}[/TEX]
Vạy có 2 giá trị của [TEX]x[/TEX] là [TEX]x= \frac{5}{2} ; x=\frac{-2}{3}[/TEX]

 

[braga]

Bài 17: Tìm các số [TEX]x,y,z[/TEX] biết:
[TEX]\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{1}{x+y+z}[/TEX]

Bài 18: Cho các số thực a,b sao cho {[TEX]a^2+a;b=b^2+b;a[/TEX]}
chưng minh : [TEX]a=b[/TEX]

 

[harrypham]

Bài 17: Tìm các số [TEX]x,y,z[/TEX] biết:
[TEX]\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{1}{x+y+z}[/TEX]

Thử sức với bài toán này xem.

Dễ dàng nhận thấy [TEX]x+y+z \neq 0[/TEX]

Từ [TEX]\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{1}{x+y+z}= \frac{(y+z+1)+(x+z+2)+(x+y-3)}{x+y+z}= \frac{2(x+y+z)}{x+y+z}=2[/TEX]

Như vậy [TEX]\frac{1}{x+y+z}=2 \Rightarrow x+y+z= \frac{1}{2} \ \ \ \ \ (1)[/TEX]

Và [TEX]\left\{\begin{matrix}y+z+1=2x & & \\ x+z+2=2y & & \\ x+y-3=2z & & \end{matrix}\right.[/TEX]
[TEX]\Rightarrow \left\{\begin{matrix}y+z=2x-1 & & \\ x+z=2y-2 & & \\ x+y=2z+3 & & \end{matrix}\right.[/TEX]

Thay những đẳng thức này vào (1) ta tìm được

[TEX]\left\{\begin{matrix}x=\frac{1}{2} & & \\ y=\frac{5}{6} & & \\ z=\frac{-5}{6} & & \end{matrix}\right.[/TEX].

 

[daovuquang]

Cho thêm bài nữa nhé.
Bài 18: cho 2 điểm A,B và 1 đường thẳng d. Hãy tìm 1 điểm M thuộc d để góc tạo bởi AM với d gấp đôi góc tạo bởi BM với d.