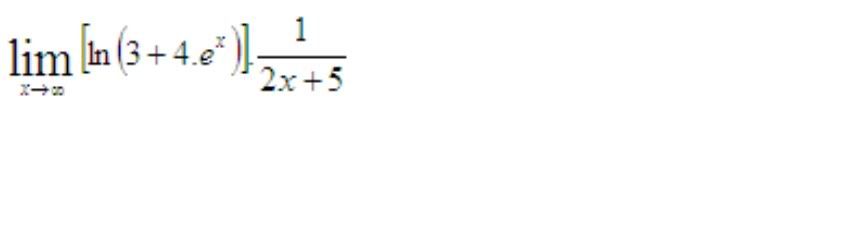anh kimxakiem và các bạn giúp em bài này ạ
tính giới hạn
+ TH 1: nếu [TEX]x\to {-}\infty[/TEX]
Khi đó
[TEX]\ln (3+4.e^x) \to \ln 3[/TEX]
[TEX]2x+5 \to {-}\infty[/TEX]
[TEX]\Rightarrow L =\lim_{x\to {-}\infty} \frac{\ln (3+4.e^x)}{2x+5} = 0[/TEX]
+ TH 2: nếu [TEX]x\to {+}\infty[/TEX]
Khi đó
[TEX]\ln (3+4.e^x) \to +\infty[/TEX]
[TEX]2x+5 \to {+}\infty[/TEX]
(dạng [TEX]\frac{\infty}{\infty}[/TEX] , áp dụng L'Hospital)
Xét [TEX]L\prime = \lim_{x\to {+}\infty} \frac{[\ln (3+4.e^x)]\prime}{[2x+5]\prime} = \lim_{x\to {+}\infty} \frac{4.e^x}{(3+4.e^x)2} = \frac{1}{2} \lim_{x\to {+}\infty} \frac{(4.e^x+3) -3}{(3+4.e^x)} = \frac{1}{2} \lim_{x\to {+}\infty}[ 1- \frac{3}{(3+4.e^x)}] = \frac{1}{2} [/TEX]
Vậy tồn tại [TEX]L\prime[/TEX] nên [TEX]L = L\prime = \frac{1}{2}[/TEX]
Chú ý quy tắc L'Hospital
Cho hai hàm [TEX]f(x)[/TEX] và [TEX]g(x)[/TEX], nếu [TEX]\lim_{x\to x_0} f(x) = \lim_{x\to x_0} g(x) = 0[/TEX] hoặc [TEX]\pm \infty[/TEX] và [TEX]\lim_{x\to x_0}\frac{f'(x)}{g'(x)}[/TEX] tồn tại (hữu hạn) thì [TEX]\lim_{x\to x_0}\frac{f(x)}{g(x)} = \lim_{x\to x_0}\frac{f'(x)}{g'(x)}[/TEX]
1, Quy tắc L'Hospital chỉ áp dụng cho dạng [TEX]\frac{0}{0}[/TEX] hoặc [TEX]\frac{\infty}{\infty}[/TEX]
2, Quy tắc nói : nếu [TEX]\lim_{x\to x_0}\frac{f'(x)}{g'(x)}[/TEX] tồn tại (hữu hạn) thì [TEX]\lim_{x\to x_0}\frac{f(x)}{g(x)} = \lim_{x\to x_0}\frac{f'(x)}{g'(x)}[/TEX] nên nếu trình bày mà viết ngay là
[TEX]L= \lim_{x\to x_0}\frac{f(x)}{g(x)} = \lim_{x\to x_0}\frac{f'(x)}{g'(x)} = \text{blah blah ...}[/TEX] là sai. Vì [TEX]\lim_{x\to x_0}\frac{f(x)}{g(x)}[/TEX] vẫn có thể tồn tại khi [TEX]\lim_{x\to x_0}\frac{f'(x)}{g'(x)}[/TEX] ko tồn tại (hoặc vô định). Khi đó L'Hospital ko áp dụng được mà phải dùng cách khác. Vì vậy nên trình bày như cách của anh ở trên:
- B1: nhận xét thấy dạng [TEX]\frac{0}{0}[/TEX] (hoặc [TEX]\frac{\infty}{\infty}[/TEX])
- B2: Xét [TEX]L'=\lim_{x\to x_0}\frac{f'(x)}{g'(x)}[/TEX], tính ra thấy nó tồn tại hữu hạn khi đó mới kết luận [TEX]L=L'[/TEX]