L
letrang3003
[tex]\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}}\frac{dx}{sin^3x}[/tex]
[tex]\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}}\frac{dx}{sin^3x}[/tex]
[TEX]=\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}}\frac{sinxdx}{sin^4x}=-\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{d(cosx)}{(1-cos^2x)^2}[/TEX][tex]\int\limits_{\frac{\pi}{4}}^{\frac{\pi}{2}}\frac{dx}{sin^3x}[/tex]
[tex]\int\limits_{0}^{1}\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}dx[/tex]
bài này khá hay
tuy anh kimxakiem 2507
từng giải rồi
nhưng vẫn đưa lên đây cho mọi người cùng làm
đặt t=thì :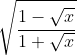
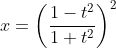
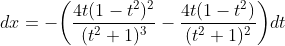
do đó ta cần tính :
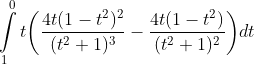
[tex]\int\limits_{0}^{1} \sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}dx[/tex]
bài này khá hay
tuy anh kimxakiem 2507
Và đây là 2 câu của tui nữa :
[TEX]I = \int\limits_{0}^{\pi}cos^nx . cosnxdx[/TEX]
[TEX]I = \int\limits_{0}^{ \frac{\pi}{2}} cos^nx . sinnxdx[/TEX]
>-
>-
>-
>-
>-

[TEX]\int_{1}^{2}\frac{dx}{x(1+x^7)} - \int_{1}^{2}\frac{x^{6}dx}{(1+x^7)}[/TEX]
Xét [TEX]\int_{1}^{2}\frac{x^{6}dx}{(1+x^7)}[/TEX]
Đặt [TEX]x^7 = t => dt = 7x^6 dx[/TEX]
cách này cũng đượcko bjk I bao nhiêu nữa ; giải quyết nốt rồi các bạn đưa đề mới nhé
đặt [TEX]t = \sqrt{x} \Rightarrow x= t^2 => dx = 2t d t[/TEX]
[TEX]I=\int_{0}^{1}\sqrt{\frac{1-t}{1+t} }2t d t[/TEX] . đặt [TEX]t = co s u => dt = - sin u du [/TEX]
\Rightarrow[TEX] I= \int\limits_{\frac{\pi}{2}}^{0} \sqrt{ \frac{1- co s u }{1+ co s u}} 2 co s u ( - sin u ) du = - 2 \int\limits_{\frac{\pi}{2}}^{0} \frac{1- co s u }{\sqrt{ 1- co s ^2 u}} sin u co s u du [/TEX]
[TEX]= 2 \int\limits_{0} ^{\frac{\pi}{2} } (1- co s u ) co s u du = 2 - \frac{\pi}{2}[/TEX]
không hiểu bài nàytổng quát
1; [TEX]I = \int\limits_{}^{}cos^nx . sinnxdx = \frac{cos^nxcosnx}{2n} + \frac{1}{2} .\int_{}^{} co s ^{ n- 1} x sin ( n- 1) x dx[/TEX]
2; [TEX]I = \int\limits_{}^{}cos^nx . cosnxdx=\frac{cos^nx sin nx}{2n} + \frac{1}{2} .\int_{}^{} co s ^{ n- 1} x cos ( n- 1) x dx[/TEX]
đặt[tex]\int\limits_{0}^{ln2}\frac{e^{2x}}{1+\sqrt{e^x-1}}dx[/tex]

