Tiếp theo ta đến với một phần khá quan trọng
Một số tập con của tập hợp số thực:
- $N* \subset N \subset Z \subset Q \subset R$
- Ký hiệu khoảng: (a ; b) = {$x \in R$| a < x < b} . Ví dụ (3;5) = {$x \in R| 3 < x < 5$}
- Nửa khoảng: [a; b) = {$x \in R|a \leq x < b$} hoặc (a; b] = {$x \in R| a < x \leq b$}, ví dụ [-2; 7) = {$x \in R| -2 \leq x < 7$}
- Đoạn: [a; b] = {$x in R |a \leq x \leq b$} [-3; 3] = {$x \in R| -3 \leq x \leq 3$}
Dạng bài toán huyền thoại thường gặp:
Cho trước A, B: định các tập hợp $A \cap B$, $A \cup B$, A \ B, B \ A
Với dạng này cách làm trực quan nhất là vẽ trục số ra:
Ví dụ: Cho A = (2; 7], B = [4; 16). Xác định các tập hợp $A \cap B$, $A \cup B$, A \ B, B \ A
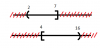
* Ta có giao 2 tập hợp chính là đoạn [4; 7], hay $A \cap B = [4; 7]$
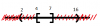
* Hợp 2 tập hợp: $A \cap B = (2; 16)$
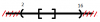
* Tính A \ B:

Sau khi gạch tất cả các phần thuộc B, không thuộc B, không thuộc A, ta có kết quả của A\B = (2;4)
Chúng ta sẽ có phần bài tập sau khi ôn tập phần này vào 20h nhé


