B
bigbang195
Cho a,b,c dương và [TEX]\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=a+b+c[/TEX]. Chứng minh:
[TEX]\frac{1}{(2a+b+c)^2}+\frac{1}{(a+2b+c)^2}+\frac{1}{(a+b+2c)^2}\leq \frac{3}{16}[/TEX].
Lời giải .
Cho a,b,c dương và [TEX]\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=a+b+c[/TEX]. Chứng minh:
[TEX]\frac{1}{(2a+b+c)^2}+\frac{1}{(a+2b+c)^2}+\frac{1}{(a+b+2c)^2}\leq \frac{3}{16}[/TEX].
phương pháp :cho [TEX]0<x1<x2<\sqrt6[/TEX]
CM
[TEX]\frac{sinx2}{sinx1}> \frac{x2-\frac{x_2^3}{3!}}{x1-\frac{x_1^3}{3!}}[/TEX]
hihi,phương pháp làm chuẩn hok cần chỉnh!phương pháp :
xét hàm [TEX]f(t)= \frac{sin t}{t - \frac{t^3}{6}}....[/TEX]vs [TEX]t \in ( 0; \sqrt6)[/TEX]
cm[TEX] f(t) [/TEX]đb hoặc nghbiến ==> đpcm
Ai lam giúp mình bài này nhá.......................?
1/Cho 3 số dương x,y,z t/m~:[TEX]\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1.CMR[/TEX]
[TEX]\sqrt{x+yz}+\sqrt{y+xz}+\sqrt{z+xy} \ge \sqrt{xyz}+\sqrt{x}+\sqrt{y}+\sqrt{z}.[/TEX]
hai bài khá hay khác:
Cho a,b,c,d>0 , Thoả mãn: a+b+c+d=4
CMR:
[tex]\frac{a}{1+b^2c}+\frac{b}{1+c^2d}+\frac{c}{1+d^2a}+\frac{d}{1+a^2b} \ge 2 [/tex]
3/ [TEX]x \in [0;2][/TEX]
CM: [TEX]\sqrt{4x-x^3 } + \sqrt{x+x^3} \leq 3\sqrt[4]{3}[/TEX]
Em thử@: Cách này thật khủng khiếp post bài mà choáng 8-}
Biết dấu "=" roài điểm rơi đi em)
sử dụng tính chất 2 số càng xính lại gần nhau thì tích của nó càng lớn1/ [TEX]a,b,c \in [1;2][/TEX]
CM: [TEX](a+b+c)(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} ) \leq 10[/TEX]
CMR: với a,b,c>0 ta có .
}}{2})
Cho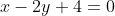
Tìm min:
[/QUOC]
[TEX]P = \sqrt{(x-3)^2+(y-6)^2}+\sqrt{(x-5)^2+(y-8)^2} [/TEX]
sử dụng mincopxki rồi từ điều kiện đưa về 1 biến
cho x,y, z .>0 CMR:
[tex]\sqrt{x^2+xy+y^2}+\sqrt{x^2+xz+z^2} \ge \sqrt{y^2+yz+z^2} [/tex]

