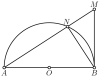
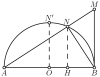
Đồng dạng: so sánh diện tích như cách mình làm ở trên. Ở đây mình so sánh với $S_{ABM}$ (mục đích là vứt tiếp điểm $N$) như sau: $$\dfrac{S_{ANB}}{S_{ABM}} = \dfrac{AB^2}{AM^2} \implies S_{ANB} = \dfrac{AB^2}{AM^2} S_{ABM}$$
Điều đặc biệt ở đây là $\dfrac{AB^2}{AM^2}$ nó không như $\dfrac14$ ở chỗ là nó
không cố định. Như vậy thì ta sẽ biến đổi nguyên một nhóm luôn chứ không riêng gì $S_{ABM}$. Để ý là $AB^2$ không đổi nên ta chỉ cần tìm $GTLN của $\dfrac{S_{ABM}}{AM^2}$.
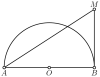
Tới đây không thể biến đổi nữa (vì quá thuận tiện rồi, hình vẽ quá gọn) mà chỉ còn cách dùng công thức diện tích thôi, và ta sẽ dùng $S_{ABM} = \dfrac12 AB \cdot BM$ cho tiện (vì $AB$ không đổi). Cuối cùng ta cần tìm GTLN của $\dfrac{BM}{AM^2}$ thôi. Dùng quan hệ hình học thì hết đường rồi, buộc lòng phải dùng cách "đại số".
Ta sẽ đặt $1$ trong hai $BM$ hoặc $AM^2$ là $x$ và tính thằng còn lại theo $x$ và các yếu tố không đổi, như bán kính $R$. Nhưng nhìn kỹ thì đặt $BM = x$ rồi tính $AM^2 = BM^2 + AB^2$ theo Pytago thì gọn hơn. Còn lại ta tìm GTLN của $$\dfrac{x}{x^2 + 4R^2}$$. Cái này thì tùy vào khả năng đại số của bạn mà làm :v có nhiều phương pháp, bạn đọc tự tìm. Mình làm theo kiểu Cô-si $$x^2 + 4R^2 \overset{Cô-si}{\geqslant} 2\sqrt{x^2 \cdot 4R^2} = 4Rx \implies \dfrac{x}{x^2+4R^2} \leqslant \dfrac1{4R}$$
Và cuối cùng ta cũng tìm được $GTLN$ của $\dfrac{x}{x^2+4R^2}$. Tới đây làm ngược lại từ từ rồi bạn sẽ tìm được GTLN của $S_{AOI}$
Một điều không thể thiếu là: giá trị lớn nhất đó đạt được khi nào (gọi tắt là dấu bằng). Dấu '=' của bđt Cô-si là $x = 2R$ tức là $M$ cách $B$ một đoạn bằng $2R$. Xong tại đây.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.