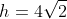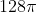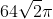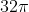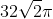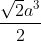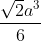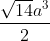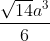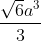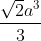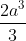Toán Cùng giải đề thi THPT Quốc gia môn Toán 2017

[huutoan00]

1/ Cho phương trình

. Khi đặt

ta được phương trình nào dưới đây:
A.

B.

C.

D.

(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

dễ dàng nhận thấy pt <=> [tex]2^{x}.2^{x} + 2.2^{x}-3=0[/tex]
=> chọn D

2/ Cho hàm số

có bảng biến thiên sau:

Mệnh đề nào sau đây là sai?
A. Hàm số có 3 điểm cực trị
B. Hàm số có giá trị cực đại bằng 3
C. Hàm số có giá trị cực đại bằng 0
D. Hàm số có 2 điểm cực tiểu
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

câu B và C không thể cùng đúng => có 1 trong 2 là sai, chỉ cần xét đến 2 câu này => xét thấy C sai

3/ Tính thể tích V của khối trụ có bán kính đáy

và

.
A. V=

B. V=

C. V=

D. V=

(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

ADCT: 4^2.pi.4v(2)=>B

5/ Cho khối chóp tứ giác đều có cạnh đáy bằng a. Cạnh bên gấp 2 lần cạnh đáy. Tính thể tích V của khối chóp đã cho
A. V =

B. V =

C. V =

D. V =

(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

đáy vuông => nửa đường chéo =a/v(2), bình phương, lấy 4(là 2^2) trừ ANS, lấy căn(được chiều cao) =>nhân 1^2, chia 3 => chọn D

8/ Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) 1 góc 30030030^0. Tính V của khối chóp.
A. V =

B. V =

C. V =

D. V =

(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

đáy vuông, cạnh 1a => chia tan30(được SB) => bình phương, trừ 1, lấy căn(được SA) => nhân 1^2 chia 3 => chọn B

 

[Thiên trường địa cửu]

Sự chuẩn bị kĩ càng sẽ là bước đệm tốt để mỗi học sinh hoàn thành bài thi vượt vũ môn một cách trọn vẹn nhất. Kì thi THPTQG năm 2017 đã lùi về quá khứ rồi. Chỉ còn 1 năm nữa thôi là lên thớt đấy mấy tình yêu 2k của tôi ơi =)))

Thôi mình vô chủ đề chính luôn Bài dành cho 2k về 3 mảng kiến thức lớp 12: Hàm số, Hình học ko gian và logarit ^^

1/ Cho phương trình [tex]4^x+2^{x+1}-3=0[/tex]. Khi đặt [tex]t=2^x[/tex] ta được phương trình nào dưới đây:
A. [tex]2t^2-3=0[/tex]
B. [tex]t^2+t-3=0[/tex]
C. [tex]4t-3=0[/tex]
D. [tex]t^2+2t-3=0[/tex]
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

2/ Cho hàm số [tex]y=f(x)[/tex] có bảng biến thiên sau:
View attachment 12315
Mệnh đề nào sau đây là sai?
A. Hàm số có 3 điểm cực trị
B. Hàm số có giá trị cực đại bằng 3
C. Hàm số có giá trị cực đại bằng 0
D. Hàm số có 2 điểm cực tiểu
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

3/ Tính thể tích V của khối trụ có bán kính đáy [tex]r=4[/tex] và [tex]h=4\sqrt{2}[/tex].
A. V= [tex]128\pi[/tex]
B. V= [tex]64\sqrt{2}\pi[/tex]
C. V= [tex]32\pi[/tex]
D. V= [tex]32\sqrt{2}\pi[/tex]
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

4/ Với a, b là các số thực dương tùy ý và [tex]a\neq 1[/tex]. Đặt [tex]P=log_ab^3+log_{a^2}b^6[/tex]. Mệnh đề nào dưới đây đúng?
A. [tex]9log_ab[/tex]
B. [tex]27log_ab[/tex]
C. [tex]15log_ab[/tex]
D. [tex]6log_ab[/tex]
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

5/ Cho khối chóp tứ giác đều có cạnh đáy bằng a. Cạnh bên gấp 2 lần cạnh đáy. Tính thể tích V của khối chóp đã cho
A. V = [tex]\frac{\sqrt{2}a^3}{2}[/tex]
B. V = [tex]\frac{\sqrt{2}a^3}{6}[/tex]
C. V = [tex]\frac{\sqrt{14}a^3}{2}[/tex]
D. V = [tex]\frac{\sqrt{14}a^3}{6}[/tex]
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

6/ Cho hàm số [tex]y=-x^3-mx^2+(4m+9)x+5[/tex] với m là tham số có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng [tex](-\infty ;+\infty )[/tex]
A. 7
B. 4
C. 6
D. 5
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

7/ Tìm giá trị thực của tham số m để phương trình: [tex]log_3^2-m.log_3x+2m-7=0[/tex] có 2 nghiệm thực [tex]x_1; x_2[/tex] thỏa mãn [tex]x_1.x_2=81[/tex]
A. m = -4
B. m = 4
C. m = 81
D. m = 44
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

8/ Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) 1 góc $30^0$. Tính V của khối chóp.
A. V = [tex]\frac{\sqrt{6}a^3}{3}[/tex]
B. V = [tex]\frac{\sqrt{2}a^3}{3}[/tex]
C. V = [tex]\frac{2a^3}{3}[/tex]
D. V = [tex]a^3\sqrt{2}[/tex]
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

9/ Cho mặt cầu (S) có R = [tex]a\sqrt{3}[/tex]. Gọi (T) là hình trụ có 2 đường tròn đáy nằm trên S và diện tích thiết diện qua trục của (T) là lớn nhất. Tính diện tích toàn phần của (T)
A. [tex]S_{tp}=9\pi a^2[/tex]
B. [tex]S_{tp}=9\pi a^2\sqrt{3}[/tex]
C. [tex]S_{tp}=6\pi a^2\sqrt{3}[/tex]
D. [tex]S_{tp}=6\pi a^2[/tex]
(Trích đề thi thử THPTQG năm 2017 - sở giáo dục Phú Thọ lần 2)

10/ Cho x,y,z là các số thực dương tùy ý hác 1 và xyz khác 1. Đặt [tex]a=log_xy[/tex], [tex]b=log_zy[/tex]. Mệnh đề nào đúng?
A. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2a}{a+b+1}[/tex]
B. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2b}{ab+a+b}[/tex]
C. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2a}{ab+a+b}[/tex]
D. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2b}{a+b+1}[/tex]
( Trích đề thi thử THPTQG năm 2017 - sở giáo dục Phú Thọ lần 2)

Mời 2k vào thử sức @LN V @huutoan00 @batman1907 @Khởi Đầu Mới @Thiên trường địa cửu @naive_ichi @Trọng Thảo


Và tiếp đó là bài cho 2k1:

11/ Giải hệ phương trình:
[tex]\left\{\begin{matrix} x-3y+\sqrt{x^2+3y^2}=0\\ \sqrt{2y-1}+2x^2-y^2-3x+1=0 \end{matrix}\right.[/tex]

12/ Giải hệ phương trình:
[tex]\left\{\begin{matrix} y^2+8x^2=3-(1+3\sqrt[3]{y^2-1})\sqrt[3]{y^2-1}\\ 4-3\sqrt[3]{(y^2-1)^2}-2\sqrt[3]{y^2-1}=12x^2+y^2-\sqrt{1-4x^2} \end{matrix}\right.[/tex]

13/ Giải hệ phương trình:
[tex]\left\{\begin{matrix} \sqrt{x-1}(1-2y)-y+2=0\\ y(y+\sqrt{x-1}+x-4=0) \end{matrix}\right.[/tex]

14/ Giải hệ phương trình:
[tex]\left\{\begin{matrix} (53-5x)\sqrt{10-x}+(5y-48)\sqrt{9-y}=0\\ \sqrt{2x-y+6}+x^2=\sqrt{-2x+y+11}+2x+66 \end{matrix}\right.[/tex]

15/ Giải hệ phương trình:
[tex]\left\{\begin{matrix} (y-2)\sqrt{x+2}-x\sqrt{y}=0\\ \sqrt{x+1}(\sqrt{y}+1)=(y-3)(1+\sqrt{x^2+y-3x}) \end{matrix}\right.[/tex]

16/ Cho tam giác ABC nội tiếp đường tròn đường kính AD, M(3;-1) là trung điểm cạnh BC. Đường cao kẻ từ B của tam giác ABC đi qua điểm E(-1;-3), điểm F(1;3) nằm trên đường thẳng AC. Tìm tọa độ đỉnh A và viết phương trình cạnh BC biết D(4;-2)

17/ Cho tam giác ABC nội tiếp đường trong tâm I(1;2); R=5. Chân đường cao kẻ từ B, C lần lượt là H(3;3); K(0;-1). Viết phương trình đường tròn ngoại tiếp tứ giác BCHK biết A có tung độ dương.

18/ Cho tam giác ABC có đỉnh A(1;5) Tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC lần lượt là I(2;2); K(5/2;3) Tìm tọa độ B, C.

19/ Giải phương trình:
[tex]2sin^2(x-\frac{\pi }{4})-sin(2x+\frac{2017\pi }{2})=1-tanx[/tex]

20/ Giải phương trình:
[tex]\frac{(1-cosx)cosx}{(1+cosx)(1-2cosx)}=\frac{1}{tanx}(x\epsilon R)[/tex]

Rồi, mấy đứa 2k1 bay hết vô cho chị. Đứa nào còn nợ mấy bài dạo trước thì triển luôn đi =)))
@zzh0td0gzz @Trafalgar D Law @Hy Nhiên @toilatot @boyfriend905 @vuhoangnam2001

1D
2C
3B
5D
6A
8B
Mình ms học c1 giải tích thôi, có 1 số ct tra trên mạng còn lại mình chưa học hihi

 

[zzh0td0gzz]

15/ Giải hệ phương trình:

Câu like có gì sai!?

 

[zzh0td0gzz]

14/ Giải hệ phương trình:

Em làm bài nào ghi ra bài đó chứ không gộp được có gì chị châu gộp giúp nha
Từ PT (1) đặt [tex]\sqrt{10-x}=a;\sqrt{9-y}=b[/tex]
(1)<=>[tex](3+5a^2)a-(3+5b^2)b=0[/tex]
Tắt 1 bước
=>[tex]a-b=0[/tex]
<=>10-x=9-y
<=>y=x-1
Thay vào PT (2):
[tex]\sqrt{x+7}+x^2=\sqrt{10-x}+2x+66[/tex]
ĐK : [tex]-7\leq x \leq10[/tex]
<=>[tex](\sqrt{x+7}-4)+(x^2-81)-(\sqrt{10-x}-1)-(2x-18)=0[/tex]
<=>[tex]\frac{x-9}{\sqrt{x+7}+4}+(x-9)(x+9)-\frac{9-x}{\sqrt{10-x}+1}-2(x-9)=0[/tex]
<=>[tex](x-9)(...)=0[/tex]
Từ đkxđ => cái phần 3 chấm trong ngoặc đó luôn dương
<=>x=9(TM)
=>y=8(TM)

11/ Giải hệ phương trình:

11/ Giải hệ phương trình:

Từ PT(1)=>[tex](x-3y)^2=x^2+3y^2[/tex]
<=>[tex]-6xy+6y^2=0[/tex]
<=>[tex]y=0~~~or~~~x=1[/tex]
y=0 loại khi đối chiếu đkxđ ở PT (2)
x=1 ta thay ngược vào PT(1) ban đầu giải ra nghiệm y=0 hoặc y=1 sau đó thử lại nghiệm thì y=1 thõa mãn
Vậy x=y=1
Bài này thấy sao sao á -_-! sai chỗ nào chăng mà nó lại ... dễ nhưng lại ngược đời quá từ 1 PT đã suy ra nghiệm cả bài,cái PT (2) kia chỉ để thử nghiệm

 

[Nguyễn Xuân Hiếu]

12/ Giải hệ phương trình:
[tex]\left\{\begin{matrix} y^2+8x^2=3-(1+3\sqrt[3]{y^2-1})\sqrt[3]{y^2-1}\\ 4-3\sqrt[3]{(y^2-1)^2}-2\sqrt[3]{y^2-1}=12x^2+y^2-\sqrt{1-4x^2} \end{matrix}\right.[/tex]
13/ Giải hệ phương trình:
[tex]\left\{\begin{matrix} \sqrt{x-1}(1-2y)-y+2=0\\ y(y+\sqrt{x-1}+x-4=0) \end{matrix}\right.[/tex]

E tham gia với nhé.
Đặt $\left\{\begin{matrix}
&\sqrt[3]{y^2-1}=a(a \geq -1) \\
&\sqrt{1-4x^2}=b(b \geq 0 )
\end{matrix}\right.$
Thay vào hệ tương đương:
$\left\{\begin{matrix}
&a^3+3a^2+a=2b^2 \\
&a^3+2a+3a^2=3b^2+b
\end{matrix}\right.$
Lấy trên trừ dưới $a=b^2+b$. Từ đây dễ thấy $a \geq 0$
$a^3+3a^2+a=2b^2
\\\Leftrightarrow (b^2+b)^3+2(b^2+b)^2+(b^2+b)^2+b^2+b=2b^2
\\\Leftrightarrow b^3(b+1)^3+2b^2(b+1)^2+b^4+2b^3+2b^2+b=2b^2
\\\Leftrightarrow b^3(b+1)^3+2b^2(b+1)^2+b^4+2b^3+b=0
\\\Leftrightarrow b(.......+1)=0$
Tới đây do $b \geq 0$ nên cái trong ngoặc $>0$ do đó $b=0$
$b=0 \Rightarrow a=0$.
Thay vào ta sẽ được nghiệm $y^2=1,x^2=\dfrac{1}{4} \Rightarrow |y|=1,|x|=\dfrac{1}{2}|$
Bài 13:
Cái dưới phải là $y(y+\sqrt{x-1})+x-4=0$ mới đúng.
Đặt $\sqrt{x-1}=a(a \geq 0),y=b$.
Phương trình tương đương:
$\left\{\begin{matrix}
&a-2ab-b+2=0(*) \\
&b^2+ab+a^2-3=0(**)
\end{matrix}\right.$
Bằng pp hệ sô bất định ta có:
$3(*)+2(**) \Leftrightarrow 2b^2-4ab+2a^2+3a-3b=0 \Leftrightarrow (b-a)(2b-2a+3)=0$.
Tới đây thì dễ rồi.
P/s: @Baoriven anh tham gia cho vui nhé :v

 

[zzh0td0gzz]

13/ Giải hệ phương trình:

Bài này dấu ngoặc nó bị lộn nhưng theo hướng làm là rút [tex]\sqrt{x-1}=\frac{y-2}{1-2y}[/tex]
và thay xuống dưới ta được PT bậc 4,từ PT bậc 4 ấn máy tính nhẩm nghiệm kiểu gì cũng ra

19/ Giải phương trình:

19/ Giải phương trình:

ngại tìm đkxđ
ĐK cần để x là nghiệm của PT là:
[tex](sinx-cosx)^2-sin(2x+\frac{\pi}{2})=1-tanx[/tex]
<=>[tex](sinx-cosx)^2-cos2x=1-tanx[/tex]
<=>[tex](sinx-cosx)^2-cos^2x+sin^2x+tanx-1=0[/tex]
<=>[tex]2sin^2x-2sinxcosx+\frac{sinx-cosx}{cosx}=0[/tex]
<=>[tex](sinx-cosx)(2sinx+\frac{1}{cosx})=0[/tex]
<=>sinx=cosx hoặc [tex]2sinxcosx=-1[/tex] ---(2sinxcosx=sin2x)---
Từ đây giải ra và do chưa tìm ĐKXĐ nên phải thử lại vào PT ban đầu(ĐK đủ)

 

[Khởi Đầu Mới]

9/ Cho mặt cầu (S) có R = [tex]a\sqrt{3}[/tex]. Gọi (T) là hình trụ có 2 đường tròn đáy nằm trên S và diện tích thiết diện qua trục của (T) là lớn nhất. Tính diện tích toàn phần của (T)
A. [tex]S_{tp}=9\pi a^2[/tex]
B. [tex]S_{tp}=9\pi a^2\sqrt{3}[/tex]
C. [tex]S_{tp}=6\pi a^2\sqrt{3}[/tex]
D. [tex]S_{tp}=6\pi a^2[/tex]
(Trích đề thi thử THPTQG năm 2017 - sở giáo dục Phú Thọ lần 2)

Giải câu khó nhất

Gọi r, h lần lượt là bán kính đáy và chiều cao của hình trụ.
Ta có:
[tex](\frac{h}{2})^2+r^2=R^2\rightarrow \frac{h}{2}=\sqrt{(a\sqrt{3})^2-r^2}\rightarrow h=2\sqrt{3a^2-r^2}[/tex]
Diện tích thiết diện qua trục là:
[tex]S=2\sqrt{3a^2-r^2}.2r=4r\sqrt{3a^2-r^2}\leq 2(r^2+3a^2-r^2)=6a^2[/tex]
Dấu "=" xảy ra
[tex]\Leftrightarrow r=\sqrt{3a^2-r^2}\Leftrightarrow r=\frac{a\sqrt{6}}{2}\rightarrow h=a\sqrt{6}[/tex]
Diện tích toàn phần:
[tex]S_{tp}=2\pi .(\frac{a\sqrt{6}}{2})^2+2\pi .(\frac{a\sqrt{6}}{2}).a\sqrt{6}=9\pi a^2[/tex]

=> Chọn A

1D
2C
3B
5D
6A
8B
Mình ms học c1 giải tích thôi, có 1 số ct tra trên mạng còn lại mình chưa học hihi

Giải chi tiết ra đi. Chứ giải vậy làm sao biết sai ở đâu mà sửa đc?

 

[batman1907]

4/ Với a, b là các số thực dương tùy ý và [tex]a\neq 1[/tex]. Đặt [tex]P=log_ab^3+log_{a^2}b^6[/tex]. Mệnh đề nào dưới đây đúng?
A. [tex]9log_ab[/tex]
B. [tex]27log_ab[/tex]
C. [tex]15log_ab[/tex]
D. [tex]6log_ab[/tex]
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)

7/ Tìm giá trị thực của tham số m để phương trình: [tex]log_3^2-m.log_3x+2m-7=0[/tex] có 2 nghiệm thực [tex]x_1; x_2[/tex] thỏa mãn [tex]x_1.x_2=81[/tex]
A. m = -4
B. m = 4
C. m = 81
D. m = 44
(Trích đề thi THPTQG năm 2017 - BGD - mã 101)


10/ Cho x,y,z là các số thực dương tùy ý hác 1 và xyz khác 1. Đặt [tex]a=log_xy[/tex], [tex]b=log_zy[/tex]. Mệnh đề nào đúng?
A. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2a}{a+b+1}[/tex]
B. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2b}{ab+a+b}[/tex]
C. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2a}{ab+a+b}[/tex]
D. [tex]log_{xyz}(y^3x^2)=\frac{3ab+2b}{a+b+1}[/tex]
( Trích đề thi thử THPTQG năm 2017 - sở giáo dục Phú Thọ lần 2)

Mời 2k vào thử sức @LN V @huutoan00 @batman1907 @Khởi Đầu Mới @Thiên trường địa cửu @naive_ichi @Trọng Thảo

4.
Với những bài như thế này ta chỉ mất khoảng dưới 30s để biết đáp án bằng mẹo sử dụng máy tính.
-Nhập biểu thức P vào máy tính rồi gán vào a,b các giá trị thoả mãn điều kiện đề bài, chẳng hạn như ta chọn a=2, b=3. Ta tính được $P=9,509775004$
-Ta thử: $A=9log_{a}b=9log_{2}3=14,26466251>P$
==> Đáp án đúng là D
7.
Theo Vi-ét ta có: $log_{3}x_{1}+log_{3}x_{2}=m=log_{3}(x_{1}.x_{2})=4$==> Đáp án B
10.
-Với cách thử tương tự bài 4, ta chọn x=2, y=3, z=4
-Gán các giá trị $A=log_{2}3, B=log_{4}3$
-Tính giá trị biểu thức $P=log_{2.3.4}(3^3.2^2)$
-Đối chiếu với các đáp án A,B,C,D ta được B là đáp án đúng.

 

[Thiên trường địa cửu]

Giải câu khó nhất

Gọi r, h lần lượt là bán kính đáy và chiều cao của hình trụ.
Ta có:
[tex](\frac{h}{2})^2+r^2=R^2\rightarrow \frac{h}{2}=\sqrt{(a\sqrt{3})^2-r^2}\rightarrow h=2\sqrt{3a^2-r^2}[/tex]
Diện tích thiết diện qua trục là:
[tex]S=2\sqrt{3a^2-r^2}.2r=4r\sqrt{3a^2-r^2}\leq 2(r^2+3a^2-r^2)=6a^2[/tex]
Dấu "=" xảy ra
[tex]\Leftrightarrow r=\sqrt{3a^2-r^2}\Leftrightarrow r=\frac{a\sqrt{6}}{2}\rightarrow h=a\sqrt{6}[/tex]
Diện tích toàn phần:
[tex]S_{tp}=2\pi .(\frac{a\sqrt{6}}{2})^2+2\pi .(\frac{a\sqrt{6}}{2}).a\sqrt{6}=9\pi a^2[/tex]

=> Chọn A

Giải chi tiết ra đi. Chứ giải vậy làm sao biết sai ở đâu mà sửa đc?

Mình có giải bài ra đâu, tại nó dài quá không có tgian nên toàn bấm máy tính thôi, nên không biêt giải thích kiểu gì cho cam. Bạn cứ xem có đúng ko là ok hihi

#Châu Cậu làm đúng rồi. Bây giờ cậu trình bày câu 6 theo hình thức tự luận cho mình nhé. Còn 6 câu kia có Toàn làm cả rồi ^^

 

[Thiên trường địa cửu]

Mình có giải bài ra đâu, tại nó dài quá không có tgian nên toàn bấm máy tính thôi, nên không biêt giải thích kiểu gì cho cam. Bạn cứ xem có đúng ko là ok hihi

#Châu Cậu làm đúng rồi. Bây giờ cậu trình bày câu 6 theo hình thức tự luận cho mình nhé. Còn 6 câu kia có Toàn làm cả rồi ^^

Thực ra câu 6 mình đã từng chữa cho 1 bạn trên dd nên mình nhớ rõ đáp án, không cần tính, nhưng cậu yêu cầu nên mình vẫn lôi máy tính vs bút ra làm hihi

 

[zzh0td0gzz]

20/ Giải phương trình:

cô đơn quá 2k1 bỏ bạn bè thế này à
[tex]\frac{cosx(cosx-1)^2}{sin^2x(1-2cosx)}=\frac{cosx}{sinx}[/tex]
<=>[tex](cosx-1)^2=sinx(1-2cosx)[/tex](Khi tìm ĐKXĐ thì bạn sẽ suy được sinx và cosx khác 0)
---Giải lượng giác bí quá đưa về ẩn phụ ---
Đặt sinx=a
Bây giờ xét 2 trường hợp cosx âm và cosx dương,mình làm cos dương còn âm tương tự nhé
*)Giả sử cosx>0
=>[tex](\sqrt{1-a^2}-1)^2=a(1-2\sqrt{1-a^2})[/tex]
<=>[tex]2-a^2-2\sqrt{1-a^2}=a-2a\sqrt{1-a^2}[/tex]
<=>[tex](-a^2-a+2)+(2a\sqrt{1-a^2}-2\sqrt{1-a^2})=0[/tex]
Rồi các đồng chí tự giải tiếp nhé,do mình chưa tìm đkxđ nên sau khi ra nghiệm thử lại coi nhá
*)giả sử cosx<0(tự giải nhé ^^)
--->nhớ là mình đã nêu sin cos khác 0 ròi nha đừng bắt bẻ vì sao lại không thể bằng 0(vì có tan và 1/tan đó )

 

[linkinpark_lp]

Hình như các bài toán hình học phẳng kết hợp thêm tính chất hình học này làm các cao thủ "tham số hóa" của chúng ta chùn tay ah? để mình đưa ra 1 số gợi ý các bạn thử làm xem có ra không nhá

 

[zzh0td0gzz]

Hình như các bài toán hình học phẳng kết hợp thêm tính chất hình học này làm các cao thủ "tham số hóa" của chúng ta chùn tay ah? để mình đưa ra 1 số gợi ý các bạn thử làm xem có ra không nhá
View attachment 12368

T.T á á á.....bài mới đê ace ơi

#Châu Bài cũ mềm rồi em ạ. Nếu thích e cứ giải đi, tối nay chị đưa bài mới lên nhé ^^

 

[linkinpark_lp]

THÔNG BÁO:
Như các bạn đã biết nhóm mình lập ra với mục đích là giải đề thi THPT Quốc gia môn toán năm vừa rồi, mặc dù kỳ thi đã kết thúc được 1 tuần nhưng mình thấy nhóm vẫn hoạt động tốt và có ích cho các bạn khóa mới nên nhóm mình vẫn sẽ tiếp tục hoạt động nhưng sẽ có thay đổi 1 chút. Bây giờ đang trong thời gian nghỉ hè và kỳ thi THPT Quốc gia tiếp theo phải chờ hơn 300 ngày nữa mới đến nên mình quyết định trong thời gian này nhóm sẽ chuyển sang ôn tập và làm các bài tập theo từng chương giống như chương trình học ở trường, sẽ có chia ra bài tập cho từng khối 10, 11 và 12 giúp các bạn ôn tập hoặc các bạn đang có ý định học trước chương trình năm sau có thể làm quen với các dạng bài đã được dùng trong bài thi đại học các năm trước. Các bài sẽ có độ khó tăng dần và dù câu hỏi dễ hay là trắc nghiệm thì mình mong các bạn nên trích dẫn câu hỏi và trình bày rõ cách làm để cho mọi người có thể xem cách các bạn tư duy từ đó áp dụng cho các bài toán khác, đây cũng chính là phương châm hoạt động của nhóm mình nhằm hỗ trợ các thành viên hết sức có thể. Cuối cùng mình xin gửi lời cảm ơn tới tất cả các bạn đã đồng hành với nhóm trong thời gian qua, hy vọng các bạn sẽ tiếp tục đồng hành cùng nhóm và làm cho box toán cũng như diễn đàn Hocmai.vn mãi là ngôi trường chung của học trò Việt.

 

[linkinpark_lp]

CHƯƠNG MỞ ĐẦU

 

[zzh0td0gzz]

Đề lớp 10
Câu 1:đk: xy khác 0
[tex]x-\frac{1}{x}=y-\frac{1}{y}[/tex]
<=>[tex](x-y)+(-\frac{1}{x}+\frac{1}{y})=0[/tex]
<=>[tex](x-y)(1+\frac{1}{xy})=0[/tex]
<=>x=y hoặc xy=-1
*)x=y =>[tex]x^3-2x+1=0[/tex]
<=>[tex](x-1)(x^2+x-1)=0[/tex]
.............
*)xy=-1 <=>[tex]y=-\frac{1}{x}[/tex]
=>[tex]x^3+\frac{2}{x}+1=0[/tex]
<=>[tex]x^4+x+2=0[/tex]
<=>[tex](x^2+x+1)(x^2-x+2)=0[/tex]
............
Câu 2:ĐK: [tex]x\geq y ;x+y\geq-2[/tex]
PT (1) <=>[tex](x-y)^2=(x-y)^3[/tex]
<=>[tex](x-y)^2(x-y-1)=0[/tex]
*)x=y
=>[tex]2x=\sqrt{2x+2}[/tex]
Bình phương và ...
*)x=y+1
=>[tex]2y+1=\sqrt{2y+3}[/tex]
Bình phương và ...
Câu 3: ĐK: [tex]x\geq \frac{-1}{2}[/tex]
ĐK cần
bình phương :
[tex]x^2+mx+2=4x^2+4x+1[/tex]
<=>[tex]3x^2+(4-m)x-1=0[/tex]
Do a và c trái dấu nên PT luôn có 2 nghiệm PB
ĐK đủ: Đặt y=x+0,5 => [tex]y\geq0[/tex]
<=>x=y-0,5
Bây giờ thay y vào và giải PT ẩn theo vi-ét sao cho tổng và tích 2 nghiệm dương ta sẽ tìm được điều kiện của m
-----------------LOADING-------------------------------------

 

[zzh0td0gzz]

ĐỀ LỚP 10:
Câu 4:
ĐK:[tex]x\leq\frac{6}{5}[/tex]
[tex](2\sqrt[3]{3x-2}+4)+(3\sqrt{6-5x}-12)=0[/tex]
<=>[tex]2\frac{3x+6}{\sqrt[3]{(3x-2)^2}-2\sqrt[3]{3x-2}+4}+3\frac{-5x-10}{\sqrt{6-5x}+4}=0[/tex]
<=>x=-2 hoặc [tex]\frac{6}{\sqrt[3]{(3x-2)^2}-2\sqrt[3]{3x-2}+4}-\frac{15}{\sqrt{6-5x}+4}=0[/tex]
Dù biết cái vế kia bé hơn 0 mà bó tay rồi
Câu 5: ĐKXĐ: [tex]-\frac{1}{3}\leq x \leq 6[/tex]
[tex]\sqrt{3x+1}-\sqrt{6-x}+x^2-14x-8=0[/tex]
<=>[tex](\sqrt{3x+1}-4)-(\sqrt{6-x}-1)+(x^2-14x-5)=0[/tex]
<=>[tex]\frac{3x-15}{\sqrt{3x+1}+4}-\frac{5-x}{\sqrt{6-x}+1}+(x-5)(3x+1)=0[/tex]
<=>[tex](x-5)(\frac{3}{\sqrt{3x+1}+4}+\frac{1}{\sqrt{6-x}+1}+3x+1)=0[/tex]
Chứng minh đường cái ngoặc dài dài kia luôn dương nhờ ĐKXĐ =>x=5

 

[batman1907]

CHƯƠNG MỞ ĐẦU

Câu 11:
Vì đồ thị có tính đối xứng nên có dạng hàm trùng phương: $y=ax^{4}+bx^{2}+c$
Như vậy ta loại ngay được A và C.
Ta thấy đồ thị cắt trục hoành tại 2 điểm phân biệt nên phương trình: $ax^{4}+bx^{2}+c=0$ phải có 2 nghiệm phân biệt==> Chọn B
Câu 12:
$y^{'}=3x^{2}+3> 0$
Vậy hàm số đồng biến trên R==> Chọn C
Câu 13:
$y=\frac{(x-4)(x+1)}{(x-4)(x+4)}=\frac{x+1}{x+4}$
Vậy đồ thị có 1 tiệm cận ngang y=1 và 1 tiệm cận đứng x=-4
==>Chọn A
Câu 14:
Để hàm số nghịch biến thì:
$y^{'}=\frac{-4x}{x^{2}+1}< 0\Leftrightarrow x> 0$
==> Chọn A
Câu 15:
Ta thử từ giá trị m nhỏ nhất là m=-2: giải phương trình: $x^{3}-7x^{2}+11x-2=-2\Rightarrow x=0$(thoả mãn)
==> Chọn C
Câu 16:
y xác định$\Leftrightarrow x-1> 0\Leftrightarrow x> 1$
==> Chọn B
Câu 17:
Ta dễ dàng đưa f(x) về dạng: $f(x)=3x+5cosx+a$
$f(0)=10\Leftrightarrow 5+a=10\Leftrightarrow a=5$
==> Chọn A
Câu 18:
Vì đường thẳng x=1 là tiệm cận đứng của đồ thị nên ta loại ngay 2 đáp án A,B
$y^{'}=\frac{ad-bc}{(cx+d)^{2}}$
Giả sử $a> 0$.
Vì đồ thị cắt trục hoành tại điểm có hoành độ âm nên b> 0
Tiệm cận ngang của đồ thị là $y=k=\frac{a}{c}>0$ nên a và c cùng dấu$\Rightarrow c> 0$
Tiệm cận đứng của đồ thị là $x=1=\frac{-d}{c}> 0$ nên d và c trái dấu$\Rightarrow d< 0$
$\Rightarrow ad-bc< 0\Rightarrow y^{'}< 0$
==> Chọn D
Câu 20:
$y^{'}=-3x^{2}-2mx+4m+9$
Hàm số nghịch biến trên R$\Leftrightarrow y^{'}< 0$
$\Leftrightarrow \left\{\begin{matrix} &-3< 0 \\ &\Delta ^{'}< 0 \end{matrix}\right.$
$\Rightarrow \Delta ^{'}=m^{2}+3(4m+9)=m^{2}+12m+27< 0$
$\Leftrightarrow -9< m< -3$
==> Chọn D
Câu 21:
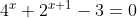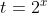
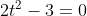
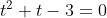
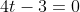
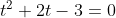
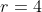Chia y cho $y^{'}$ rồi lấy phần dư ta được phương trình AB có dạng: $y=-8x-2$
==> Chọn C

 

[linkinpark_lp]

Bài làm của @batman1907 rất tuyệt vời, chỉ có 2 câu sau hơi nhầm lẫn 1 tí

Câu 13:
$y=\frac{(x-4)(x+1)}{(x-4)(x+4)}=\frac{x+1}{x+4}$
Vậy đồ thị có 1 tiệm cận ngang y=1 và 1 tiệm cận đứng x=-4
==>Chọn A

câu này em làm đúng rồi nhưng lại không chú ý kĩ yêu cầu đề bài nó chỉ hỏi có bao nhiêu tiệm cận ĐỨNG thôi chứ không phải có bao nhiêu tiệm cận nên đáp án chính xác câu này là C nhá

Câu 20:
$y^{'}=-3x^{2}-2mx+4m+9$
Hàm số nghịch biến trên R$\Leftrightarrow y^{'}< 0$
$\Leftrightarrow \left\{\begin{matrix} &-3< 0 \\ &\Delta ^{'}< 0 \end{matrix}\right.$
$\Rightarrow \Delta ^{'}=m^{2}+3(4m+9)=m^{2}+12m+27< 0$
$\Leftrightarrow -9< m< -3$
==> Chọn D

câu này điều kiện để hàm y luôn đồng biến hoặc nghịch biến phải là delta nhỏ hơn hoặc bằng 0 chứ nhỉ?

 

[Nguyễn Xuân Hiếu]

ĐỀ LỚP 10:
Câu 4:
ĐK:[tex]x\leq\frac{6}{5}[/tex]
[tex](2\sqrt[3]{3x-2}+4)+(3\sqrt{6-5x}-12)=0[/tex]
<=>[tex]2\frac{3x+6}{\sqrt[3]{(3x-2)^2}-2\sqrt[3]{3x-2}+4}+3\frac{-5x-10}{\sqrt{6-5x}+4}=0[/tex]
<=>x=-2 hoặc [tex]\frac{6}{\sqrt[3]{(3x-2)^2}-2\sqrt[3]{3x-2}+4}-\frac{15}{\sqrt{6-5x}+4}=0[/tex]
Dù biết cái vế kia bé hơn 0 mà bó tay rồi
Câu 5: ĐKXĐ: [tex]-\frac{1}{3}\leq x \leq 6[/tex]
[tex]\sqrt{3x+1}-\sqrt{6-x}+x^2-14x-8=0[/tex]
<=>[tex](\sqrt{3x+1}-4)-(\sqrt{6-x}-1)+(x^2-14x-5)=0[/tex]
<=>[tex]\frac{3x-15}{\sqrt{3x+1}+4}-\frac{5-x}{\sqrt{6-x}+1}+(x-5)(3x+1)=0[/tex]
<=>[tex](x-5)(\frac{3}{\sqrt{3x+1}+4}+\frac{1}{\sqrt{6-x}+1}+3x+1)=0[/tex]
Chứng minh đường cái ngoặc dài dài kia luôn dương nhờ ĐKXĐ =>x=5

Nếu không biết chứng minh vô nghiệm thì có cách khác:
Đặt: $(\sqrt[3]{3x-2},\sqrt{6-5x}) \rightarrow (a,b) $.
Khi đó phương trình đưa về hệ:
$\left\{\begin{matrix}
&2a+3b-8=0 \\
&5a^3+3b^2=8
\end{matrix}\right.$
Rút $b$ ở phương trình đầu thay xuống phương trình $2$.
$5a^3+3(\dfrac{8-2a}{3})^2-8=0
\\\Rightarrow 15a^3+64-32a+4a^2-24=0
\\\Rightarrow 15a^3+4a^2-32a+40=0
\\\Rightarrow (a+2)(15a^2-26a+20)=0$
Dễ thấy $15a^2-26a+20$ vô nghiệm do $\Delta<0$.
Do đó $a=-2$ thay vào giải được $x=-2$(thỏa mãn)