[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
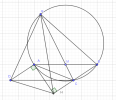
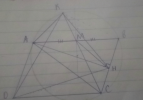
Cho hình bình hành [imath]ABCD[/imath] có [imath]\widehat{BAD} > 90^o[/imath]. Gọi [imath]H[/imath] là chân đường vuông góc kẻ từ [imath]A[/imath] đến [imath]BC[/imath]. Đường trung tuyến kẻ từ [imath]C[/imath] của tam giác [imath]ABC[/imath] cắt đường tròn ngoại tiếp [imath]\Delta ABC[/imath] tại [imath]K[/imath], CMR: 4 điểm [imath]K;H;C;D[/imath] cùng thuộc 1 đường tròn
Dạ em cảm ơn ạ.^^ Em cần gấp lắm ạ.
Dạ em cảm ơn ạ.^^ Em cần gấp lắm ạ.
Attachments
Last edited by a moderator: