H
huynhbachkhoa23
Cho $x,y,z \in \mathbb{R}$ và $x+y+z=10$
Tìm GTNN của $A=x^2+6y+15z^4$
Tìm GTNN của $A=x^2+6y+15z^4$
Last edited by a moderator:
Làm kĩ hộ em thế nào để ra phần này với. Em cũng đặt như thế nhưng bị tịt phần ra thế kia.
What the ......................... :|
Bài của em đơn giản hơn nhiều :|
Bài 1:Thay $x=1-y$ :|
Bài 2: Thay $a=\dfrac{x}{y}; b=\dfrac{y}{z}; c=\dfrac{z}{x}$ và biến đổi thành:
$x^3+y^3+z^3+3xyz \ge xy(x+y)+yz(y+z)+zx(z+x)$ (Schur bậc 3) :|
Làm kĩ hộ em thế nào để ra phần này với. Em cũng đặt như thế nhưng bị tịt phần ra thế kia.
Làm kĩ hộ em thế nào để ra phần này với. Em cũng đặt như thế nhưng bị tịt phần ra thế kia.
ủng hộ topic 1 bài, dễ hơn mấy bài bác Khoa đăng=))
Đề: Cho $x, y, z >0$ thỏa mãn $xy+yz+zx=1$, chứng minh:
$$\dfrac{\sqrt{x^2+1}\sqrt{y^2+1}}{\sqrt{z^2+1}} + \dfrac{\sqrt{y^2+1}\sqrt{z^2+1}}{\sqrt{x^2+1}} + \dfrac{\sqrt{z^2+1}\sqrt{x^2+1}}{\sqrt{y^2+1}} \ge 2\sqrt{3}$$
ủng hộ topic 1 bài, dễ hơn mấy bài bác Khoa đăng=))
Đề: Cho $x, y, z >0$ thỏa mãn $xy+yz+zx=1$, chứng minh:
$$\dfrac{\sqrt{x^2+1}\sqrt{y^2+1}}{\sqrt{z^2+1}} + \dfrac{\sqrt{y^2+1}\sqrt{z^2+1}}{\sqrt{x^2+1}} + \dfrac{\sqrt{z^2+1}\sqrt{x^2+1}}{\sqrt{y^2+1}} \ge 2\sqrt{3}$$
Cái (1)cm sao vậy bạn giúp mình đi:-SS=((=([TEX] (\frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b})+ (\frac{c}{a+c}+\frac{a}{a+b}+\frac{b}{b+c})=\frac{a+b}{b+c}+\frac{b+c}{a+c}+\frac{a+c}{a+b} \geq3(1)[/TEX]
[TEX](\frac{a}{a + c} + \frac{b}{a + b} + \frac{c}{b + c})+(\frac{c}{a+c}+\frac{a}{a+b}+\frac{b}{b+c})=3(2)[/TEX]
[TEX](1)(2) \Rightarrow dpcm[/TEX]
Mình sửa lại này! Bạn nên đọc trong nội quy mà anh Hải đưa cho khi là thành viên mới...Cho a,b là 2 số dương phân biệt tuỳ ý
Đặt: A= (a+b)/2 B= căn ab
Chứng minh: B < (a-b)^2/8(A-B) < A
Xin lỗi mk ko bt gõ latex j j đó mk đang cố hx.....
Mk cảm ơn....Mình sửa lại này! Bạn nên đọc trong nội quy mà anh Hải đưa cho khi là thành viên mới...
Cho a,b là 2 số dương phân biệt tuỳ ý
Đặt;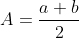
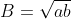
Chứng minh :^2}{8(A-B)}%3CA)
b/4a hay là b/(4a+b^2) bạnCho 2 số thực a,b thỏa mãn [tex]a+b\geq 1[/tex] , a>0
Tìm GTNN của [tex]A=8a^2+b/4a +b^2[/tex]
dạ (8a^2+b)/4a +b^2 ạb/4a hay là b/(4a+b^2) bạn
ráng làm vậyhêhê, bài mình tự chế này:
Cho a,Tìm GTLN: