.
Một con lắc đồng hồ được coi như 1 con lắc đơn có chu kì dao động T = 2s, vật nặng có khối lượng m = 1kg.
Biên độ góc dao động lúc đầu là anpha_o = 5 độ
. Do chịu tác dụng của một lực cản không đổi FC = 0,011(N) nên nó chỉ dao động
được một thời gian t(s) rồi dừng lại. Xác định t.
A: t = 20s B: t = 80s C: t = 40s D: t = 10s
anh rocky giải chi tiết giúp e bài này nhé
Ban đầu năng lượng con lắc: [TEX]W_0=mgl(1-\cos\alpha_0)\approx \frac{1}{2}mgl\alpha_0^2[/TEX] (do [TEX]\alpha_0[/TEX] nhỏ, chú ý là đo bằng rad nhé)
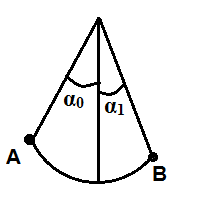
Sau nửa chu kỳ đầu thì biên độ góc mới là [TEX]\alpha_1 (\alpha_1 <\alpha_0)[/TEX]. Năng lượng mới là [TEX]W_1=\frac{1}{2}mgl\alpha_1^2[/TEX]
Độ giảm cơ năng: [TEX]\Delta W= W_0-W_1=\frac{1}{2}mgl(\alpha_0^2-\alpha_1^2)[/TEX] (1)
Công của lực cản sau nửa chu kỳ đầu tiên: [TEX]W_c=F_c.S=F_cl(\alpha_0+\alpha_1)[/TEX] (2)
Từ (1) và (2) ta có: [TEX]\frac{1}{2}mgl(\alpha_0^2-\alpha_1^2)=F_cl(\alpha_0+\alpha_1)[/TEX]
Sử dụng hằng đẳng thức: [TEX]a^2-b^2=(a-b)(a+b)[/TEX]. Rồi biến đổi linh tinh, cuối cùng rút ra:
[TEX]\alpha_0-\alpha_1=\frac{2F_c}{mg}[/TEX]
Đó là độ giảm biên độ góc sau nửa chu kỳ dao động -> thực hiện cả 1 chu kỳ dao động nó sẽ giảm
[TEX]\Delta \alpha =\frac{4F_c}{mg}[/TEX]
Vật dừng lại khi tổng độ giảm biên độ góc = [TEX]\alpha_0[/TEX]. Nên số chu kỳ vật thực hiện được cho đến khi dừng hẳn là:
[TEX]N=\frac{\alpha_0}{\Delta \alpha}=\frac{mg\alpha_0}{4F_c}\approx 19,833\approx 20[/TEX] chu kỳ. Vậy [TEX]t=40 (s)[/TEX]