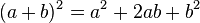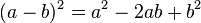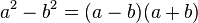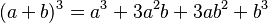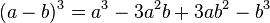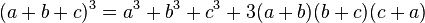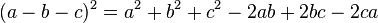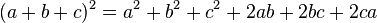- 3 Tháng một 2015
- 2,257
- 2,499
- 574
- 23
- Bắc Giang
- Trường Đại học Ngoại Ngữ - Đại học Quốc Gia Hà Nội
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hello các bạn !
Hè đến rồi, mọi người đã phóng biển lớn trèo núi cao ở đâu chưa ? Tớ vẫn ngồi ở nhà -_- TT^TT , ai cùng hoàn cảnh với tớ thì tham gia topic này để tự kiếm việc để làm nhé
Nói vui vậy thoi →_→ , HM bây giờ rảnh quá nên mình mở topic mog tất cả bà con cô bác họ hàng xa vào đây cùng giải toán ý mà
Topic mở ra nhằm cùng mọi người ôn tập lại kiến thức lớp 8, sẽ có các bài từ cơ bản đến nâng cao, về sau sẽ có cả chương trình lớp 9 để mọi người làm quen nữa đấy! Các bạn năm nay lên lớp 8 cũng cùng tham gia nhé!
Game start à nhầm -_-....topic start!!!!
* bug hoa _ tung lụa* * vỗ tay _ bộp _ bộp :v *
Hè đến rồi, mọi người đã phóng biển lớn trèo núi cao ở đâu chưa ? Tớ vẫn ngồi ở nhà -_- TT^TT , ai cùng hoàn cảnh với tớ thì tham gia topic này để tự kiếm việc để làm nhé
Nói vui vậy thoi →_→ , HM bây giờ rảnh quá nên mình mở topic mog tất cả bà con cô bác họ hàng xa vào đây cùng giải toán ý mà
Topic mở ra nhằm cùng mọi người ôn tập lại kiến thức lớp 8, sẽ có các bài từ cơ bản đến nâng cao, về sau sẽ có cả chương trình lớp 9 để mọi người làm quen nữa đấy! Các bạn năm nay lên lớp 8 cũng cùng tham gia nhé!
Game start à nhầm -_-....topic start!!!!
* bug hoa _ tung lụa* * vỗ tay _ bộp _ bộp :v *
Last edited: