bài 1 bạn làm rõ được khong ạ1/$x=\sqrt{2+\dfrac{10+2\sqrt{5}{4}}+\sqrt{2-\dfrac{10+2\sqrt{5}{4}}-\sqrt{\dfrac{6-2\sqrt{5}{2}}-1$
Ở đây xuất hiện các hđt,bạn rút gọn rồi thay $x$ vào
2/Bạn giải pt
$x^2+x-2=0$
Nghiệm pt là tọa độ gđ 2 đồ thị
3/a/Rút gọn bình thường
b/xét P và $\sqrt{P}$ chú ý P với 0;P với 1
Toán Toán ôn thi lớp 10
- Thread starter thanhbinh2002
- Ngày gửi
- Replies 33
- Views 2,715
-
- Tags
- @iceghost
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Giúp mình mấy bài này nữa
1) Cho
[tex]x = \sqrt{2 + \sqrt{ \frac{5 + \sqrt{5}}{2}}} + \sqrt{2 - \sqrt{ \frac{5 + \sqrt{5}}{2}}} - \sqrt{3 - \sqrt{5}} - 1[/tex]
Tính giá trị của biểu thức [tex]A = 2 x ^{3} + 3 x ^{2} - 4 x + 2[/tex]
2) Cho (P) [tex]y = x ^{2}[/tex] và (d) y = - x + 2. Tìm tọa độ giao điểm của (d) và (P)
3) Cho biểu thức: [tex]P = \left ( \frac{ \sqrt{x} + \sqrt{y}}{1 - \sqrt{x y}} + \frac{ \sqrt{x} - \sqrt{y}}{1 + \sqrt{x y}} \right ) : \left ( 1 + \frac{x + y + 2 x y}{1 - x y} \right )[/tex]
a) Rút gọn P
b) So sánh P và [tex]\sqrt{P}[/tex]
Attachments
bài 1 mình chưa hiểu lắm tại sao [tex]x = \left ( \left ( \sqrt{3 + \sqrt{5}} \right ) - \left ( \sqrt{3 + \sqrt{5}} \right ) \right ) ^{2} - 1[/tex]
Ah,sorry,lỗi kĩ thuật,bạn cứ nhân tử và mẫu của biểu thức với $\sqrt{2}$ là xuất hiện các hằng đẳng thức để rút gọn thôi.bài 1 bạn làm rõ được khong ạ
bài 1 mình chưa hiểu lắm tại sao [tex]x = \left ( \left ( \sqrt{3 + \sqrt{5}} \right ) - \left ( \sqrt{3 + \sqrt{5}} \right ) \right ) ^{2} - 1[/tex]
Attachments
Cho tam giác ABC vuông tại A; AB = 15cm; AC = 20cm. Dựng đường tròn tâm (O) đk AB và đường tròn tâm (O') đk AC. Chúng cắt nhau tại D
a) CM D nằm trên BC
b) Gọi M là điểm chính giữa cung DC nhỏ. AM cắt DC tại E và cắt (O) tại N. CM DE . AC = AE . MC
c) CM AN = EN
d) CM O,N,O' thẳng hàng
e) Gọi I là trung điểm MN. CM góc OIO' = 90o
g) Tính diện tích tam giác AMC
a) CM D nằm trên BC
b) Gọi M là điểm chính giữa cung DC nhỏ. AM cắt DC tại E và cắt (O) tại N. CM DE . AC = AE . MC
c) CM AN = EN
d) CM O,N,O' thẳng hàng
e) Gọi I là trung điểm MN. CM góc OIO' = 90o
g) Tính diện tích tam giác AMC
2) Tìm m để A lớn nhất
[tex]A = \frac{2 m + 1}{m ^{2} + 2}[/tex]
Attachments
bạn giúp mình bài hình được không???
Cho tam giác ABC vuông tại A; AB = 15cm; AC = 20cm. Dựng đường tròn tâm (O) đk AB và đường tròn tâm (O') đk AC. Chúng cắt nhau tại D
a) CM D nằm trên BC
b) Gọi M là điểm chính giữa cung DC nhỏ. AM cắt DC tại E và cắt (O) tại N. CM DE . AC = AE . MC
c) CM AN = EN
d) CM O,N,O' thẳng hàng
e) Gọi I là trung điểm MN. CM góc OIO' = 90o
g) Tính diện tích tam giác AMC
- 23 Tháng bảy 2016
- 1,123
- 1,495
- 344
- 23
- Đắk Nông
a)Dễ thấy $\widehat{CDA}=90^0,\widehat{ADB}=90^0$(góc nt chắn nửa đường tròn)bạn giúp mình bài hình được không???
Do đó $\widehat{CDA}+\widehat{ADB}=180^0$.
Hay $C,D,B$ thẳng hàng hay $D$ nằm trên $BC$
b)Do $M$ là điểm chính giữa nên $\widehat{CAM}=\widehat{EAD}$.
Do đó dễ dàng cm dc tam giác $AMC$ đồng dạng tam giác $ADE$ nên $DE.AC=AE.MC$
c)$\widehat{NED}=\widehat{EAC}+\widehat{ECA}=\widehat{EAD}+\widehat{DAO}=\widehat{NAB}$.
$\Rightarrow \triangle EBA$ cân mặt khác $BN$ vuông góc $EA$.
Do đó $NA=NE$
d)Dễ thấy $O',N,O$ lần lượt là trung điểm của $AC,AE,AB$.
Nên $O'O//BC$ và $O'N//BC$(đường trung bình )
Do đó theo tiên đề Ơ-clit thì $O',N,O$ thẳng hàng.
e)Nối $O'$ với $M$ ta có:$O'C=O'D,MC=MD$ nên $O'M$ là đường trung trực của $CD$.
Mà $O'N//CD \Rightarrow \widehat{MO'N}=90^0$.
Do $I$ là trung điểm của cạnh huyền $MN$ nên: $\widehat{IO'N}=\widehat{INO'}=\widehat{ANO}=\widehat{NAO}$.
Do đó tg $O'IOA$ nt
Mà $\widehat{O'AO}=90^0 \Rightarrow O'IO=90^0(dpcm)$
f) Câu này khá dễ bạn tự làm nhé áp dụng diện tích tam giác vuông là ok
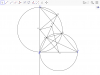
câu f mình ra đáp án 79,66 mà không biết đúng hay saia)Dễ thấy $\widehat{CDA}=90^0,\widehat{ADB}=90^0$(góc nt chắn nửa đường tròn)
Do đó $\widehat{CDA}+\widehat{ADB}=180^0$.
Hay $C,D,B$ thẳng hàng hay $D$ nằm trên $BC$
b)Do $M$ là điểm chính giữa nên $\widehat{CAM}=\widehat{EAD}$.
Do đó dễ dàng cm dc tam giác $AMC$ đồng dạng tam giác $ADE$ nên $DE.AC=AE.MC$
c)$\widehat{NED}=\widehat{EAC}+\widehat{ECA}=\widehat{EAD}+\widehat{DAO}=\widehat{NAB}$.
$\Rightarrow \triangle EBA$ cân mặt khác $BN$ vuông góc $EA$.
Do đó $NA=NE$
d)Dễ thấy $O',N,O$ lần lượt là trung điểm của $AC,AE,AB$.
Nên $O'O//BC$ và $O'N//BC$(đường trung bình )
Do đó theo tiên đề Ơ-clit thì $O',N,O$ thẳng hàng.
e)Nối $O'$ với $M$ ta có:$O'C=O'D,MC=MD$ nên $O'M$ là đường trung trực của $CD$.
Mà $O'N//CD \Rightarrow \widehat{MO'N}=90^0$.
Do $I$ là trung điểm của cạnh huyền $MN$ nên: $\widehat{IO'N}=\widehat{INO'}=\widehat{ANO}=\widehat{NAO}$.
Do đó tg $O'IOA$ nt
Mà $\widehat{O'AO}=90^0 \Rightarrow O'IO=90^0(dpcm)$
f) Câu này khá dễ bạn tự làm nhé áp dụng diện tích tam giác vuông là ok
View attachment 11575
giúp mình ạ
1) Cho pt [tex]x ^{2} - 2 m x + 1 = 0[/tex] . Tìm m để pt có 2 nghiệm phân biệt [tex]x _{1} ; x _{2}[/tex] mà [tex]\frac{ \sqrt{x _{1}}}{x _{2}} + \frac{ \sqrt{x _{2}}}{x _{1}} = m + 1[/tex]
2) cho [tex]a ; b \neq 0[/tex] và [tex]\frac{1}{a} + \frac{1}{b} = \frac{1}{2}[/tex]
CM pt [tex]\left ( x ^{2} + a x + b \right ) \left ( x ^{2} + b x + a \right ) = 0[/tex] luôn có nghiệm
3) Tính
[tex]P = \frac{ \sqrt{ \sqrt{5} + 2} + \sqrt{ \sqrt{5} - 2}}{\sqrt{ \sqrt{5} + 1}} - \sqrt{ 3 - 2 \sqrt{2}}[/tex]
4) Cho 2 đường tròn (O;R) và (O';r) cắt nhau tại A;B (R>r). Vẽ tiếp tuyến chung ngoài CD cắt đường thẳng AB tại K ( C thuộc (O) ; D thuộc (O')). Hai điểm O;O' nằm khác phía với đường thẳng AB tại K
a) CM [tex]KC ^{2} = KA . KB[/tex]
b) Đường thẳng qua C song song với AD cắt đường thẳng qua D song song với AC tại E. CM K là trung điểm của AE
c) CM BE < R + r
5) Cho nửa đường tròn (O;R). Đường kính AD cố định. Vẽ tứ giác ABCD nội tiếp nửa (O;R). Gọi I là giao điểm của AC và BD. K là hình chiếu của I trên AD.
a) CM I là tâm đường tròn nội tiếp tam giác BCK
b) Gọi F là giao điểm của CK và BD. CM BI . DF = BD . IF
c) Gọi E là trung điểm của ID. CM [tex]ED ^{2} = EB . EF[/tex]
d) Xác định vị trí lớn nhất của B để bán kính đường tròn nội tiếp tam giác ABC lớn nhất. Tính giá trị lớn nhất đó
@Nguyễn Xuân Hiếu @Otaku8874
1) Cho pt [tex]x ^{2} - 2 m x + 1 = 0[/tex] . Tìm m để pt có 2 nghiệm phân biệt [tex]x _{1} ; x _{2}[/tex] mà [tex]\frac{ \sqrt{x _{1}}}{x _{2}} + \frac{ \sqrt{x _{2}}}{x _{1}} = m + 1[/tex]
2) cho [tex]a ; b \neq 0[/tex] và [tex]\frac{1}{a} + \frac{1}{b} = \frac{1}{2}[/tex]
CM pt [tex]\left ( x ^{2} + a x + b \right ) \left ( x ^{2} + b x + a \right ) = 0[/tex] luôn có nghiệm
3) Tính
[tex]P = \frac{ \sqrt{ \sqrt{5} + 2} + \sqrt{ \sqrt{5} - 2}}{\sqrt{ \sqrt{5} + 1}} - \sqrt{ 3 - 2 \sqrt{2}}[/tex]
4) Cho 2 đường tròn (O;R) và (O';r) cắt nhau tại A;B (R>r). Vẽ tiếp tuyến chung ngoài CD cắt đường thẳng AB tại K ( C thuộc (O) ; D thuộc (O')). Hai điểm O;O' nằm khác phía với đường thẳng AB tại K
a) CM [tex]KC ^{2} = KA . KB[/tex]
b) Đường thẳng qua C song song với AD cắt đường thẳng qua D song song với AC tại E. CM K là trung điểm của AE
c) CM BE < R + r
5) Cho nửa đường tròn (O;R). Đường kính AD cố định. Vẽ tứ giác ABCD nội tiếp nửa (O;R). Gọi I là giao điểm của AC và BD. K là hình chiếu của I trên AD.
a) CM I là tâm đường tròn nội tiếp tam giác BCK
b) Gọi F là giao điểm của CK và BD. CM BI . DF = BD . IF
c) Gọi E là trung điểm của ID. CM [tex]ED ^{2} = EB . EF[/tex]
d) Xác định vị trí lớn nhất của B để bán kính đường tròn nội tiếp tam giác ABC lớn nhất. Tính giá trị lớn nhất đó
@Nguyễn Xuân Hiếu @Otaku8874
Mk chụp hơi mờ, srgiúp mình ạ
1) Cho pt [tex]x ^{2} - 2 m x + 1 = 0[/tex] . Tìm m để pt có 2 nghiệm phân biệt [tex]x _{1} ; x _{2}[/tex] mà [tex]\frac{ \sqrt{x _{1}}}{x _{2}} + \frac{ \sqrt{x _{2}}}{x _{1}} = m + 1[/tex]
2) cho [tex]a ; b \neq 0[/tex] và [tex]\frac{1}{a} + \frac{1}{b} = \frac{1}{2}[/tex]
CM pt [tex]\left ( x ^{2} + a x + b \right ) \left ( x ^{2} + b x + a \right ) = 0[/tex] luôn có nghiệm
3) Tính
[tex]P = \frac{ \sqrt{ \sqrt{5} + 2} + \sqrt{ \sqrt{5} - 2}}{\sqrt{ \sqrt{5} + 1}} - \sqrt{ 3 - 2 \sqrt{2}}[/tex]
4) Cho 2 đường tròn (O;R) và (O';r) cắt nhau tại A;B (R>r). Vẽ tiếp tuyến chung ngoài CD cắt đường thẳng AB tại K ( C thuộc (O) ; D thuộc (O')). Hai điểm O;O' nằm khác phía với đường thẳng AB tại K
a) CM [tex]KC ^{2} = KA . KB[/tex]
b) Đường thẳng qua C song song với AD cắt đường thẳng qua D song song với AC tại E. CM K là trung điểm của AE
c) CM BE < R + r
5) Cho nửa đường tròn (O;R). Đường kính AD cố định. Vẽ tứ giác ABCD nội tiếp nửa (O;R). Gọi I là giao điểm của AC và BD. K là hình chiếu của I trên AD.
a) CM I là tâm đường tròn nội tiếp tam giác BCK
b) Gọi F là giao điểm của CK và BD. CM BI . DF = BD . IF
c) Gọi E là trung điểm của ID. CM [tex]ED ^{2} = EB . EF[/tex]
d) Xác định vị trí lớn nhất của B để bán kính đường tròn nội tiếp tam giác ABC lớn nhất. Tính giá trị lớn nhất đó
@Nguyễn Xuân Hiếu @Otaku8874
Attachments
giúp mình ạ
1) Cho pt [tex]x ^{2} - 2 m x + 1 = 0[/tex] . Tìm m để pt có 2 nghiệm phân biệt [tex]x _{1} ; x _{2}[/tex] mà [tex]\frac{ \sqrt{x _{1}}}{x _{2}} + \frac{ \sqrt{x _{2}}}{x _{1}} = m + 1[/tex]
2) cho [tex]a ; b \neq 0[/tex] và [tex]\frac{1}{a} + \frac{1}{b} = \frac{1}{2}[/tex]
CM pt [tex]\left ( x ^{2} + a x + b \right ) \left ( x ^{2} + b x + a \right ) = 0[/tex] luôn có nghiệm
3) Tính
[tex]P = \frac{ \sqrt{ \sqrt{5} + 2} + \sqrt{ \sqrt{5} - 2}}{\sqrt{ \sqrt{5} + 1}} - \sqrt{ 3 - 2 \sqrt{2}}[/tex]
4) Cho 2 đường tròn (O;R) và (O';r) cắt nhau tại A;B (R>r). Vẽ tiếp tuyến chung ngoài CD cắt đường thẳng AB tại K ( C thuộc (O) ; D thuộc (O')). Hai điểm O;O' nằm khác phía với đường thẳng AB tại K
a) CM [tex]KC ^{2} = KA . KB[/tex]
b) Đường thẳng qua C song song với AD cắt đường thẳng qua D song song với AC tại E. CM K là trung điểm của AE
c) CM BE < R + r
5) Cho nửa đường tròn (O;R). Đường kính AD cố định. Vẽ tứ giác ABCD nội tiếp nửa (O;R). Gọi I là giao điểm của AC và BD. K là hình chiếu của I trên AD.
a) CM I là tâm đường tròn nội tiếp tam giác BCK
b) Gọi F là giao điểm của CK và BD. CM BI . DF = BD . IF
c) Gọi E là trung điểm của ID. CM [tex]ED ^{2} = EB . EF[/tex]
d) Xác định vị trí lớn nhất của B để bán kính đường tròn nội tiếp tam giác ABC lớn nhất. Tính giá trị lớn nhất đó
@Nguyễn Xuân Hiếu @Otaku8874
Câu 4:
a. [tex]\Delta AKC[/tex] [tex]\sim[/tex] [tex]\Delta CKB[/tex] (gg)
-> [tex]KC^{2}=KA.KB[/tex]
b. CMTT câu a có [tex]KD^{2}=KA.KB[/tex]
-> KD=KC
Xét tứ giác CEDA có: CE // AD, AC//DE
-> CEDA là hình bình hành
Mà K là trung điểm CD
-> K là trung điểm AE
c EB cắt OO' tại T
-> Dễ CM T là trung điểm AB Và OO' vuông góc AB tại T
-> KT = 1/2 EB
Lấy T' là trung điểm OO'
Có CO//DO' ( cùng vuông góc với CD )
->OCDO' là hình thang
Có K, T' lần lượt là trung điểm CD và OO'
-> KT' là đg trung bình -> KT' = 1/2 ( OC+O'D ) =1/2 (R+r)
Có KT' [tex]\geq[/tex] KT ( đg xiên, đg vuông góc)
-> KT [tex]\leq[/tex] 1/2 (R+r)
-> BE [tex]\leq[/tex] R+r
Dấu '=' xảy ra khi T' trùng T -> OT=O'T -> R = r









