Bài toán chứng minh [imath]9,(9)=10[/imath] , lỗi sai: cách làm có vẻ đã được đề cập trong sách NCPT lớp 7 - Vũ Hữu Bình. Rằng hiện tại chưa có phép tính cộng trừ cho số vô hạn tuần hoàn bằng cách tính như trên, nên nó sai. Cơ sở: cách làm của bạn Phương ở trên nếu [imath]n[/imath] là vô hạn được gọi là cách chứng minh biến đổi số họcBạn phản bác cái gì v ?
Chỉ rõ giúp mình nó ở bài toán nào, chỗ nào và cơ sở tại sao lập luận mình sai
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Cho em hỏi là chỗ sai ở đâu vậy ạ?Bài toán chứng minh [imath]9,(9)=10[/imath] , lỗi sai: cách làm có vẻ đã được đề cập trong sách NCPT lớp 7 - Vũ Hữu Bình. Rằng hiện tại chưa có phép tính cộng trừ cho số vô hạn tuần hoàn bằng cách tính như trên, nên nó sai. Cơ sở: cách làm của bạn Phương ở trên nếu [imath]n[/imath] là vô hạn được gọi là cách chứng minh biến đổi số học
Mình có mở ngoặc ghi n chữ số 9 đó bạn ơiBạn lấy sô nào thì nó vẫn là hữu hạn, không khác nhau về ý nghĩa với số nhỏ hơn, bài toán vẫn vô nghĩa, nếu là hữu hạn rõ ràng bạn phải ký hiệu [imath]n[/imath] số [imath]9[/imath] chứ không phải là [imath]...[/imath] tượng trưng cho vô hạn, lỗi sai ở đó chứ không phải bắt đầu từ phép trừ.
nếu n thuộc N, thì 10a - a = 89.9...1,chị đã sửa thành n chữ số 9, [imath]n\in \mathbb{N}[/imath], thì nó không là phép cọng trừ số vô hạn tuần hoàn, em có thể lí giải đúng/sai không
sai vì 99,99..9 (có n-1 chữ số 9 sau dấu ,)- 9,99..9( có n chữ số 9 sau dấu ,) khác 90. Do đó phép chứng minh sai
vì khi a x 10 lên thì hàng thập phân sẽ mất 1 số 9 thì lúc đặt phép trừ sẽ thành 99,9...0 - 9.9...9 = 89.9...1( em trình bày theo cách hiểu của mình, có sai góp ý để em biết với ạ)
Thử suy diễn ra cho trường hợp [imath]n[/imath] tiến ra vô hạn thử nàonếu n thuộc N, thì 10a - a = 89.9...1,
vì khi a x 10 lên thì hàng thập phân sẽ mất 1 số 9 thì lúc đặt phép trừ sẽ thành 99,9...0 - 9.9...9 = 89.9...1( em trình bày theo cách hiểu của mình, có sai góp ý để em biết với ạ)
AUGUSTIN CAUCHY
Augustin-Louis Cauchy (1789-1857), nhà Toán học lớn của Pháp, một thành viên của Viện Hàn Lâm Khoa học đáng kính. Ít ai biết được cuộc đời và sự nghiệp đầy trắc trở của ông.
Gia đình Cauchy rất xùng đạo Công giáo. Khác với người cha, Cauchy không thay đổi theo trào lưu chính trị mới. Đây cũng là một trong những nguyên nhân ông không hòa hợp được với giới chức địa phương cũng như lãnh đạo nơi ông làm (khi đó ông đang làm kỹ sư). Ngoài ra, quan hệ xã hội trong nghề nghiệp phức tạp khiến ông thấy chán nản với công việc. Trong hơn 2 năm làm việc tại Cherbourg ông dành nhiều thời gian cho việc nghiên cứu Toán.
Từ năm 1813 đến năm 1815, Cauchy đã ghi danh ba lần vào danh sách dự tranh vào Hàn Lâm Viện Khoa Học. Tuy nhiên ông trượt cả ba với số phiếu áp đảo. Lí do dẫn tới những thất bại không phải vì năng lực của ông mà là vì yếu tố chính trị. Hầu hết các thành viên của Viện Hàn Lâm đều trung thành với phe Cộng Hòa, còn Cauchy lại không dấu diếm rằng mình là người bảo hoàng và là một tín đồ Công giáo. Còn một lí do nữa là sự quá nổi tiếng của Cauchy và sự tự tin hay nói quá là kiêu căng đã làm cho các thành viên đương chức không hài lòng.
Khi nhà nước Phục hoàng lên nắm quyền vào năm 1815, một tình huống thuận lợi xuất hiện cho con đường công danh của Cauchy. Vua và cận thần rất ấn tượng với thành tự của các nhà toán học và khoa học tự nhiên. Trong hoàn cảnh ấy, Cauchy là nhà toán học sánh chói và hết mực trung thành với hoàng gia, xứng đáng thay thế cho các nhà bác học “phản động” kia. Cuối cùng, Cauchy được vào Viện Hàn Lâm không phải bằng bầu cử mà bằng sắc lệnh của vua. Mặc cho có nhiều nhà toán học dè biểu, xa lánh nhưng không ai có thể phủ nhận những công trình toán học của ông, ông hoàn toàn xứng đáng ngồi ở vị trí ấy.
Cauchy cũng được bổ nhiệm về trường Đại học Bách khoa. Năm 1816, ông đề nghị cải cách chương trình toán, năm nhất là phải đào sâu vào nội dung toán thuần túy (giải tích), đưa cơ học và những phần áp dụng vào giảng dạy ở năm thứ hai. Điều này đi ngược với truyền thống xem toán học như là một phương tiện cung cấp cho vật lý và các môn kỹ thuật. Dù bị từ chối nhưng ông vẫn cải cách, tự sửa đổi chương trình các lớp ông phụ trách. Đúng là một vị giáo sư bướng bỉnh …
Cuối tháng 7-1830, vua Charles rời Paris, một tuần sau Louis Philippe, quận công Orléans, được đưa lên ngôi vua nước Pháp. Chế độ mới được thành lập theo ý phe Cộng hòa. Đạo luật mới buộc mọi công chức phải thề trung thành với chế độ mới. Cauchy vội vã rời khỏi Paris trước khi bị bắt buộc phải đọc lời thề đáng nguyền rủa ấy.
Ngày 22/10/1838, sau 8 năm vắng mặt, Cauchy trở lại Viện Hàn Lâm, tham dự cuộc họp đầu tiên. Đây là bước đầu trong chiến dịch phục hồi vị trí và uy tín của mình mà ông đã đánh mất.
Tháng 5 năm 1857, cảm thấy sức khỏe yếu dần do bệnh sưng khớp, Cauchy rời Paris về tịnh dưỡng ở Sceaux, miền ngoại ô phía nam Paris. Ngày 24/5/1857 ông qua đời tại đây, thọ gần 68 tuổi.
(GS Nguyến Tiến Dũng viết)
Đóng góp lớn nhất của Cauchy trong toán học là việc xây dựng môn Giải tích (bao gồm giải tích phức và phương trình vi phân) thành lý thuyết toán học chặt chẽ, với các khái niệm và ngôn ngữ hiện đại được dùng đến ngày nay. Nhưng Cauchy là một nhà toán học toàn tài, và ngoài giải tích, ông còn có đóng góp lớn vào nhiều lĩnh vực toán học khác, như đại số, lý thuyết số, hình học không gian, hình học vi phân, và lý thuyết xác suất.
Ở đây tôi chỉ tóm tắt một số điều của cuộc đời ông. Mời các bạn đọc thêm: “Thiên tài và số phận: Chuyện kể về các nhà toán học”. Hi vọng nó sẽ tiếp thêm niềm đam mê và hứng thú với các bạn đối với Toán học.
Một câu hỏi nhỏ: các bạn hãy nêu các công trình khoa học của Cauchy mà các bạn biết?
Last edited:
 Sau một thời gian mình đã quay trở lại rồi đây, các bạn cùng tìm hiểu thêm một điều mới nha
Sau một thời gian mình đã quay trở lại rồi đây, các bạn cùng tìm hiểu thêm một điều mới nhaDẢI MOBIUS
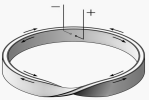
Dải Mobius hay còn gọi là mặt Mobius được đặt tên theo nhà toán học và nhà thiên văn học August Ferdinand Möbius (1790-1868), người đã đưa ra ý tưởng vào tháng 9 năm 1858.

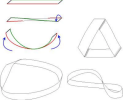
Hình vẽ trên minh họa một băng giấy được dán lại để thành một vòng. Nó sẽ có hai mặt (mặt trong và mặt ngoài). Nếu một con kiến đang bò trên mặt ngoài của vòng giấy thì các duy nhất để nó có thể bò sang mặt trong là bò qua mép của vòng giấy
Dải Mobius có thể dễ dàng được tạo ra bằng cách dùng một dải giấy và cho xoắn một nửa và sau đó dán hai đầu của dải với nhau để tạo thành một vòng. (Các bạn hãy thử làm ở nhà nhé)
Dải Mobius chỉ có một mặt. Nếu con kiến bò dọc theo dải Mobius, nó có thể bò trên toàn bộ dải này mà không cần phải bò qua mép. M.C. Escher cho thấy trong bức tranh nổi tiếng của ông, Möbius Strip II (Mão Đỏ), kiến có thể đi trên một dải Mobius trên một bề mặt duy nhất vô thời hạn. Có lẽ đó cũng là lý do tại sao biểu tượng vô cực giống với dải Mobius!
* Ứng dụng trong thực tế
1. Kiến trúc
....
2. Vật lí
- Các dải Mobius ở dây curoa của ô tô hay dây curoa cho các thiết bị cơ khí đặc biệt được quan trâm trong công nghiệp bởi chúng mòn đều hơn các dây curoa thông thường
- Điện trở Mobius
.....
3. Hóa học
- Nút thắt phân tử với các đặc tính đặc biệt
- Hạt tích điện trong từ trường của trái đất có thể di chuyển trên một dải Mobius.
.....
Còn rất nhiều ứng dụng khác nữa. Các bạn hãy cho mình biết với nhé

______________________
TLTK: Niềm vui Toán học/ Tiểu luận Dải Mobius và ứng dụng thực tế
Áp dụng luôn , ví dụ như logo của Ngân hàng Vietcombank đó ạ =))Sau một thời gian mình đã quay trở lại rồi đây, các bạn cùng tìm hiểu thêm một điều mới nha
DẢI MOBIUS
Dải Mobius hay còn gọi là mặt Mobius được đặt tên theo nhà toán học và nhà thiên văn học August Ferdinand Möbius (1790-1868), người đã đưa ra ý tưởng vào tháng 9 năm 1858.
View attachment 216130
Hình vẽ trên minh họa một băng giấy được dán lại để thành một vòng. Nó sẽ có hai mặt (mặt trong và mặt ngoài). Nếu một con kiến đang bò trên mặt ngoài của vòng giấy thì các duy nhất để nó có thể bò sang mặt trong là bò qua mép của vòng giấy
Dải Mobius có thể dễ dàng được tạo ra bằng cách dùng một dải giấy và cho xoắn một nửa và sau đó dán hai đầu của dải với nhau để tạo thành một vòng. (Các bạn hãy thử làm ở nhà nhé)
Dải Mobius chỉ có một mặt. Nếu con kiến bò dọc theo dải Mobius, nó có thể bò trên toàn bộ dải này mà không cần phải bò qua mép. M.C. Escher cho thấy trong bức tranh nổi tiếng của ông, Möbius Strip II (Mão Đỏ), kiến có thể đi trên một dải Mobius trên một bề mặt duy nhất vô thời hạn. Có lẽ đó cũng là lý do tại sao biểu tượng vô cực giống với dải Mobius!
* Ứng dụng trong thực tế
1. Kiến trúc
View attachment 216136....
Vincent Callebaut (Đài Loan)
2. Vật lí
- Các dải Mobius ở dây curoa của ô tô hay dây curoa cho các thiết bị cơ khí đặc biệt được quan trâm trong công nghiệp bởi chúng mòn đều hơn các dây curoa thông thường
- Điện trở Mobius
View attachment 216141
.....
3. Hóa học
- Nút thắt phân tử với các đặc tính đặc biệt
- Hạt tích điện trong từ trường của trái đất có thể di chuyển trên một dải Mobius.
.....
Còn rất nhiều ứng dụng khác nữa. Các bạn hãy cho mình biết với nhé
______________________
TLTK: Niềm vui Toán học/ Tiểu luận Dải Mobius và ứng dụng thực tế
Em tự đoán theo ý hiểu của em thôi , em là con người luôn tự tin đoán đại ạ =)))))))))))))
Anh cảm giác nó chỉ là chữ V khung tam giác, với một độ sâu nhất địnhÁp dụng luôn , ví dụ như logo của Ngân hàng Vietcombank đó ạ =))
Em tự đoán theo ý hiểu của em thôi , em là con người luôn tự tin đoán đại ạ =)))))))))))))
logo google driver có phải là một ví dụ không bạnAnh cảm giác nó chỉ là chữ V khung tam giác, với một độ sâu nhất định
Phân tích theo hướng suy nghĩ cũ, gg mới thì nó cơ bản chỉ là ghép 3 mảng màu , phần giao là phối màu =)logo google driver có phải là một ví dụ không bạn
 hôm nay các bạn cùng mình tìm hiểu một cấu trúc thú vị trong tự nhiên nha
hôm nay các bạn cùng mình tìm hiểu một cấu trúc thú vị trong tự nhiên nhaCẤU TRÚC TỔ ONG
Người ta thường nói ong là “nhà kiến trúc thông minh và nhà toán học đại tài”, có bạn có biết vì sao không? Chúng ta cùng tìm hiểu nhé
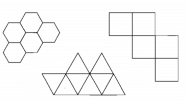
Các nhà toán học đã chứng minh rằng chỉ có các lục giác đều, hình vuông và tam giác đều là có thể ghép lại với nhau (xếp hình) trên mặt phẳng mà không để lại một khoảng trống nào.
Trong ba hình nói trên, lục giác đều có chu vi nhỏ nhất nếu diện tích của chúng bằng nhau. Điều này có nghĩa khi xây dựng các ô lục giác để làm tổ của mình, bầy ong dùng ít sáp và lao động ít hơn đối với cùng một khoảng không gian.
Ngoài ra, hình lục giác có thể dự trữ khối lượng lớn nhất với tổng số vật liệu xây dựng ít nhất. những nhà nghiên cứu khẳng định rằng cấu trúc lỗ tổ hình lục giác vừa có sức chứa tối đa lại có độ bền rất lớn. Mặc dù các thành lỗ tổ sáp chỉ dày khoảng 0.5mm, nhưng nó có thể hỗ trợ 25 lần trọng lượng của nó. Một bánh tổ ong bằng sáp mới xây chỉ nặng 150 g có thể chứa đến 3 kg mật ong mà không bị vỡ
Trong tự nhiên, còn có những cấu trúc hình lục giác khác như những bông tuyết, trong các phân tử, tinh thể, sinh vật biển và các dạng sống khác.
Ứng dụng
Do kết cấu tổ ong có lợi nhất cho việc tiết kiệm nhiên liệu và tận dụng không gian nên các nhà thiết kế, xây dựng hiện đại đã áp dụng nó trong thiết kế cánh máy bay, vách vệ tinh, tàu con thoi hay vô số cấu trúc trong nhà, đồ nội thất, gia dụng, thiết bị văn phòng, điện tử và các sản phẩm khác.
___________
 Mong bài viết này sẽ mang đến cho bạn những kiến thức hay thú vị ^^
Mong bài viết này sẽ mang đến cho bạn những kiến thức hay thú vị ^^
Last edited:
 Hôm nay chúng ta sẽ cùng nhau tìm hiểu một cách tính toán những thế kỉ trước nha
Hôm nay chúng ta sẽ cùng nhau tìm hiểu một cách tính toán những thế kỉ trước nhaTHANH NAPIER

Ngày xưa khi chưa có các loại máy tính cầm tay hiện đại như bây giờ, công việc tính toán rất phức tạp, mệt mỏi.
Đặc biệt đối với các nhà khoa học, các nhà buôn,… cần phải đối mặt với việc thực hiện các phép toán “đao to búa lớn”.
Vào thế kỉ XVII, John Napier (1550-1617), một nhà Toán học nổi tiếng người Scotland đã phát minh ra thanh napier để đơn giản hóa các phép toán bao gồm nhân, chia, lũy thừa và tìm căn.
Với sự ra đời của các máy tính hiện đại chúng cũng đã trở nên lỗi thời, tuy vậy thanh napier vẫn là công cụ tính toán tuyệt vời được sử dụng rộng rãi trong nhiều thế kỉ trước.
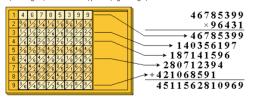
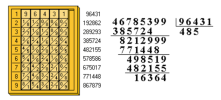
Ví dụ: nhân 298 với 7, ta sẽ xếp ba thanh 298 lại với nhau, tìm đến hàng thứ 7 rồi cọng hai số ở hàng đó lại để tìm kết quả như trong hình minh họa.
Chú ý: Nhân các số có nhiều chữ số làm tương tự nhân với một chữ số nhiều lần; phép chia cũng dùng phép nhân như trên rồi dùng phép trừ để tính số dư.
Ngoài ra ta còn có thể khai khác căn bậc 2 (vì hơi dài nên mình sẽ không nêu tại đây)
 hehe mong các bạn biết thêm được một thông tin mới nhé
hehe mong các bạn biết thêm được một thông tin mới nhé__________
TLTK: wiki/ Niềm vui Toán học
ĐỐ VUI TOÁN HỌC 1
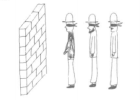
Ba người đàn ông đứng trước một bức tường
Ba người đàn ông đứng trước một bức tường
Ba người đàn ông xếp hàng thành một đường thẳng vuông góc với bức tường. Họ đều bị bịt mắt.
Sau đó, mỗi người được đội một chiếc mũ lấy ra từ một túi gồm: 3 mũ màu nâu và 2 mũ màu đen.
Ba người đàn ông được biết về thông tin này. Sau đó, các khăn bịt mắt được tháo ra. Người ta hỏi mỗi người đàn ông xem ông ta đang đội mũ màu gì.
Biết người đằng sau có thể nhìn thấy người đứng trước (ông xa tường nhất có thể nhìn thấy hai ông trên, ông đứng giữa có thể nhìn thấy ông đứng gần tường, ông đứng gần tường chỉ có thể nhìn thấy bức tường)
Người đàn ông đứng xa tường nhất nói "Tôi không biết tôi đang đội mũ màu gì"
Người đứng giữa sau khi nghe thấy câu trả lời đầu tiên thì cũng nói tương tự
Người đứng gần tường nhất sau khi nghe hai người kia đã trả lời: "Tôi biết tôi đội mũ màu gì rồi".
Ông ta đang đội mũ màu gì vậy??? Giải thích
_____________
Tham khảo: Niềm vui Toán học
Chắc 3 ông này phải thêm điều kiện là thông minh có khả năng suy luận chứ nhỉ, giả sử mấy ổng mà não nho như não mình chắc đoán đại luôn cho rồi =)))
Gọi 3 ông theo thứ tự từ bức tường trở ra là 1,2,3
Do ông 3 không biết mình đội mũ gì nên 2 ông 1, 2 không thể cùng đội mũ đen
Ông 2 cũng sẽ suy ra điều này (tức là ổng và ông 1 không cùng đội mũ đen, đồng nghĩa ít nhất 1 trong 2 phải mũ trắng)
Nếu ông 1 đội mũ đen, ông 2 sẽ lập tức suy ra mình đội mũ trắng
Mà ông 2 không biết, nên suy ra ông 1 đội mũ không phải màu đen, tức là ông 1 đội mũ màu trắng.
Gọi 3 ông theo thứ tự từ bức tường trở ra là 1,2,3
Do ông 3 không biết mình đội mũ gì nên 2 ông 1, 2 không thể cùng đội mũ đen
Ông 2 cũng sẽ suy ra điều này (tức là ổng và ông 1 không cùng đội mũ đen, đồng nghĩa ít nhất 1 trong 2 phải mũ trắng)
Nếu ông 1 đội mũ đen, ông 2 sẽ lập tức suy ra mình đội mũ trắng
Mà ông 2 không biết, nên suy ra ông 1 đội mũ không phải màu đen, tức là ông 1 đội mũ màu trắng.
Cảm ơn câu trả lời của bạn, rất chính xác nhee
Hôm nay chúng ta cùng tìm hiểu thêm về một điều mới tiếp nha
Trong toán học, ma phương (hình vuông ma thuật) là một cách sắp xếp [imath]n^2[/imath] số nguyên phân biệt trong một bảng vuông sao cho tổng [imath]n[/imath] số trên mỗi hàng, mỗi cột và đường chéo đều bằng nhau.
Ma phương chuẩn chứa các số nguyên từ 1 đến [imath]n^2[/imath]
Tồn tại ma phương chuẩn cho mọi bậc [imath]n\ge 1[/imath] trừ trường hợp [imath]n=2[/imath].
Ma phương bậc 1 là ma phương tầm thường (chứa duy nhất một ô với giá trị 1)
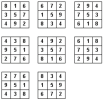
Ví dụ: Ma phương bậc 3
Hằng số (Hằng số ma thuật) trong ma phương của mỗi hàng, cột, và đường chéo. Trong ma phương chuẩn giá trị này phụ thuộc vào [imath]n[/imath] và có giá trị
[math]M=\dfrac{n(n^2+1)}2[/math]
Chứng minh: Tổng của [imath]1,2,..,n^2[/imath] là [imath]\dfrac{n^2(n^2+1)}2[/imath]
Khi đó ta có [imath]n[/imath] hàng có tổng bằng nhau nên tổng một hàng là: [imath]M=\dfrac{n(n^2+1)}2[/imath]
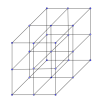
Câu hỏi: Các bạn hãy tìm khối ma phương 3x3x3 sao cho đó là khối có 27 số tự nhiên, tổng các số trên mỗi hàng hay mỗi cột ba số đều bằng 42. (Điền vào các chấm xanh)
 Các bạn hãy cùng nhau thử sức với câu hỏi này nhé
Các bạn hãy cùng nhau thử sức với câu hỏi này nhé
Hôm nay chúng ta cùng tìm hiểu thêm về một điều mới tiếp nha
MA PHƯƠNG
Trong toán học, ma phương (hình vuông ma thuật) là một cách sắp xếp [imath]n^2[/imath] số nguyên phân biệt trong một bảng vuông sao cho tổng [imath]n[/imath] số trên mỗi hàng, mỗi cột và đường chéo đều bằng nhau.
Ma phương chuẩn chứa các số nguyên từ 1 đến [imath]n^2[/imath]
Tồn tại ma phương chuẩn cho mọi bậc [imath]n\ge 1[/imath] trừ trường hợp [imath]n=2[/imath].
Ma phương bậc 1 là ma phương tầm thường (chứa duy nhất một ô với giá trị 1)
Ví dụ: Ma phương bậc 3
Hằng số (Hằng số ma thuật) trong ma phương của mỗi hàng, cột, và đường chéo. Trong ma phương chuẩn giá trị này phụ thuộc vào [imath]n[/imath] và có giá trị
[math]M=\dfrac{n(n^2+1)}2[/math]
Chứng minh: Tổng của [imath]1,2,..,n^2[/imath] là [imath]\dfrac{n^2(n^2+1)}2[/imath]
Khi đó ta có [imath]n[/imath] hàng có tổng bằng nhau nên tổng một hàng là: [imath]M=\dfrac{n(n^2+1)}2[/imath]
Câu hỏi: Các bạn hãy tìm khối ma phương 3x3x3 sao cho đó là khối có 27 số tự nhiên, tổng các số trên mỗi hàng hay mỗi cột ba số đều bằng 42. (Điền vào các chấm xanh)
 Các bạn hãy cùng nhau thử sức với câu hỏi này nhé
Các bạn hãy cùng nhau thử sức với câu hỏi này nhé
Last edited:
CÁI CHẾT CỦA ARCHIMEDES
Eureka! Eureka!… (tìm ra rồi, tìm ra rồi,…) chắc hẳn khi nghe câu nói này các bạn đã biết đấy là ai rồi nhỉ? Đó chính là Archimedes - là một nhà toán học, nhà vật lý, kỹ sư, nhà phát minh và nhà thiên văn học người Hy Lạp. Ông được coi là một trong những nhà khoa học hàng đầu của thời cổ đại.
Quê hương của ông là ở Syracuse. Trong suốt cuộc chiến tranh Punic lần thứ hai, Syracuse bị người La Mã bao vây từ năm 214TCN cho đến năm 212 TCN. Vào thời điểm đó, Archimedes đã sáng chế ra các vũ khí phòng thủ rất tài tình như máy bắn đá, ròng rọc và móc câu để kéo và phá tan thuyền của quân La Mã, kính parabol để đốt cháy thuyền. Những vũ khí này đã kìm chân quân La Mã trong gần ba năm.
Một đêm trăng sáng năm 212 trước Công nguyên, cũng là Ngày Mừng Nữ Thần Mặt Trăng ở Syracuse, khi người dân trong vùng đang say sưa với lễ hội kỷ niệm thì Archimedes nhốt mình trong căn phòng vắng và cần mẫn làm việc.
Lợi dụng sự mất cảnh giác của dân chúng nơi đây, quân La Mã đã bất ngờ đánh úp, dìm Syracuse trong biển máu. Marcus Claudius Marcellus, vị huy trưởng của quân La Mã, đã ra lệnh cho quân lính không được làm hại Archimedes. Nhưng một tên lính La Mã đã đột nhập vào nhà của Archimedes và thấy ông đang mải mê làm toán mà không hề nhận ra sự xuất hiện của hắn. Tên lính ra lệnh cho ông phải ngừng lại, nhưng Archimedes không chút để ý đến lời hắn nói. Giận dữ, tên lính đã dùng kiếm đâm chết Archimedes.
Vậy là ông đã giã từ cuộc đời này mà chưa kịp nói lời trăng trối nào.
_______________
Câu nói nổi tiếng của nhà bác học Archimedes:
Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. (Hãy cho tôi một điểm tựa, tôi sẽ nhấc bổng quả đất lên.)
CÁC KHỐI ĐA DIỆN VÀ KEPLER - POINSOT
Nhà triết học, nhà thiên văn học và cũng là nhà hình học nổi tiếng Hy Lạp – Platon (khoảng 427 – 347 TCN) tìm ra rằng chỉ có 5 khối đa diện đều. Đó là các khối tứ diện đều, lập phương, bát diện đều, mười hai mặt đều, hai mươi mặt đều.
Một điều khá thú vị là theo Plato 5 đa diện đều này còn là đại diện cho các yếu tố cơ bản trong vũ trụ:
| Yếu tố | Khối Platon |
|---|---|
| Lửa | Tứ diện đều |
| Nước | Hai mươi mặt đều |
| Không khí | Bát diện đều |
| Đất | Lập phương |
| Vũ trụ | Mười hai mặt đều |

Đặc trưng Euler: [imath]V-E+F=2[/imath] với [imath]V, E, F[/imath] lần lượt là số đỉnh, số cạnh, số mặt của khối đa diện.
Các khối trên đã được biết tới từ thời cổ đại nhưng bốn loại khối sau đây vẫn chưa được thế giới cổ đại biết tới. Kepler (1571-1630) là người đã khám phá ra hai khối đầu vào những năm 1600 và Louis Poinsot (1777-1859) khám phá lại khối này và thêm hai khối nữa vào năm 1809.
- Khối mười hai mặt sao nhỏ
- Khối mười hai mặt sao lớn
- Khối hai mươi mặt lớn
- Khối mười hai mặt lớn
Các khối này thường được sử dụng để làm các thiết bị chiếu sáng và chao đèn.
THALES và đại kim tự tháp
Thales (640-546 TCN) là nhà khoa học Hy Lạp cổ nổi tiếng, được mệnh danh là “cha đẻ của khoa học". Ông là môt nhà toán học, một thầy giáo, nhà triết học, nhà thiên văn học, một thương nhân tài ba và là nhà hình học đầu tiên đã chứng minh được các lí thuyết của mình bằng kiểu chứng minh từng bước.
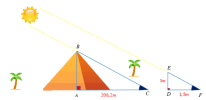
Thales đã dự đoán chính xác hiện tiện nhật thực vào năm 585 TCN và làm người Hy Lạp phải sửng sốt khi ông tính toán được chiều cao của kim tự tháo Kheops nhờ bóng của nó và tam giác đồng dạng.
Một hôm Thales đến Ai Cập cổ đại. quốc vương biết Thales đến, liền vội cho người mời ông và nói với Thales:
– Thales anh biết đấy kim tự tháp Kheops là niềm kiêu hãnh của người dân Ai Cập, nhưng mãi đến nay vẫn chưa đo được độ cao của nó. Nếu ông có thể giúp được việc này thì tất cả người dân Ai Cập sẽ biết ơn ông.
Thales nghe thấy thế không hề do dự, liền đồng ý. Ông còn nói rõ, rằng ngày hôm sau sẽ lập tức đo đạc có kết quả được.
Ông cắm một cái cọc cao 1m vuông góc với mặt đất và đo được bóng của cọc trên mặt đất là 1.5m và chiều dài bóng của Kim tự tháp trên mặt đất là 208.2m. Khi đó chiều dài của Kim tự tháp là
[math]\dfrac{AB}{AC}=\dfrac{DE}{DF}\Rightarrow AB=\dfrac{DE.AC}{DF}=138.8m[/math]
Vậy là ta đã đo được chiều cao của Kim tự tháp rồi!!