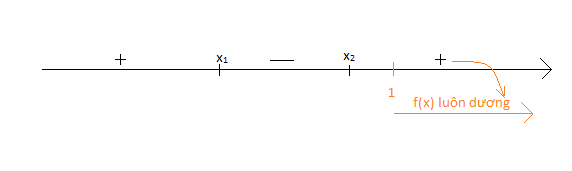P
pekon2508
Với bài toán như này thì đầu tiên bạn phải nói Xét bài toán ngược lại tìm m để bpt dã cho vô nghiệm.rồi chia 2 TH.
TH1 m=3.ta có 11<0 \Rightarrowm=3 k t\m
TH2 m # 3
f(x)=(m-3)x^2 - 2(m-3) + 3m + 2
f(x)<0 vô nghiệm \Leftrightarrow f(x)\geq0 \forallx thuộc R
\Leftrightarrowm-3>0 và denta' = -2m^2 + m +15 \leq 0
\Rightarrowm > 3
Vậy ...... có nghiệm \Leftrightarrow m thuộc {R\(3;+\infty)
TH1 m=3.ta có 11<0 \Rightarrowm=3 k t\m
TH2 m # 3
f(x)=(m-3)x^2 - 2(m-3) + 3m + 2
f(x)<0 vô nghiệm \Leftrightarrow f(x)\geq0 \forallx thuộc R
\Leftrightarrowm-3>0 và denta' = -2m^2 + m +15 \leq 0
\Rightarrowm > 3
Vậy ...... có nghiệm \Leftrightarrow m thuộc {R\(3;+\infty)
hn3 : Bạn đó làm đúng trước em rồi ^^
Last edited by a moderator: