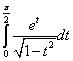Tích phân

K

kiburkid

u = x
dv = ln(...)dx ---> v = (2x+1) / (x^2+x+1)
Tách ra làm 2x/(x^2+x+1) + 1/(x^2+x+1)
rồi làm như bình thường
 
N

ngoisaohieulongtoi92

kiburkid said:
u = x
dv = ln(...)dx ---> v = (2x+1) / (x^2+x+1)
Tách ra làm 2x/(x^2+x+1) + 1/(x^2+x+1)
rồi làm như bình thường
Bấm để xem đầy đủ nội dung ...
bình thường là như thế nào em?e giải ra kết quả đi;)).....em tách thế có mà tết pháp cũng k giải ra

chị giải tiếp cho chủ thớt dễ hiểu nhé

(2x+1)dx chính là d(x^2+x+1) đấy e ah:).vì đạo hàm của x^2+x+1 =2x+1:D.đến đây mới đc nói là dễ nhé:).đáp án là vế uv/- ln(x^2+x+1)/
em thế cận vào là xong:)
 
Last edited by a moderator:
L

lantrinh93

mình làm thế này :
đặt [TEX]u = ln(x^2 +x+1)[/TEX]
[TEX]du =\frac{2x+1}{x^2+x+1}dx[/TEX]
[TEX]dv= xdx..> v =\frac{x^2}{2}[/TEX]
[TEX]I= \frac{1}{2}ln3- \int_{0}^{1}1/2.\frac{2x^3+x^2}{x^2+x+1}dx[/TEX]
[TEX]= \frac{1}{2}ln3-\frac{1}{2}I1[/TEX]

tính I 1
[TEX]I 1= \int_{0}^{1}(2x-1)+\frac{-x+1}{x^2+x+1}dx[/TEX]

chỉ mình tính cái[TEX] \int_{0}^{1}\frac{-x+1}{x^2+x+1}dx [/TEX]với :((
 
N

nhoc_maruko9x

Ôi trời kiểu gì mà đặt [tex]dv = ln(x^2+x+1)dx[/tex] rồi lại lấy đạo hàm thế kia? Thế là đạo hàm cấp 2 à? Bài này cứ đặt uv thôi, nhưng quan trọng là lấy nguyên hàm của xdx như thế nào để khi nhân vdu nó ra đẹp. Cái này mới khó, chưa nghĩ ra :))

Bài của kiburkid là gì thế? Nhìn khó hiểu quá.
 
K

kenylklee

lantrinh93 said:
chỉ mình tính cái[TEX] \int_{0}^{1}\frac{-x+1}{x^2+x+1}dx [/TEX]với :((
Bấm để xem đầy đủ nội dung ...
eq.latex

eq.latex

Rồi hết rồi, còn gì để nói nữa đâu, hì hì

Biển học vô biên, quay đầu là giường.
images
 
Last edited by a moderator:
K

kenylklee

mars.pipi said:
[TEX] \int_{0}^{1}\frac{-x+1}{x^2+x+1}dx = \int_{0}^{1}\frac{-(2x+1)}{2(x^2+x+1)}dx + \int_{0}^{1}\frac{3}{2(x^2+x+1)}dx [/TEX]

giải [TEX]\int_{0}^{1}\frac{3}{2(x^2+x+1)}dx [/TEX]

đặt [TEX](x+1/2) =\sprt{3}/2tant[/TEX]
Bấm để xem đầy đủ nội dung ...
Bạn ơi bạn sai rồi kìa, phải là -3 lần cái tích phân đằng sau mới đúng, xem lại i, mình cũng xuýt sai ó, tính toán cấp 1 cũng hok nên thân, hic hic@-). Ý, sorry bạn, đúng òy. hì hì
 
Last edited by a moderator:
K

kenylklee

Em xin trình bày một dạng tích phân khá hay, và vô cùng lạ lẫm, tìm Max, Min của tích phân, em không dám là bài kia đâu, vì em không chắc có đúng hay không, khảo sát nó khó quá, em sợ mình làm sai.
Tìm Max, Min của
[TEX]\int_{0}^{1}\left({x}^{4}-3x+1;{x}^{3}-3 \right)dx[/TEX]

Đặt: [TEX]f\left(x \right)={x}^{4}-3x+1[/TEX]
[TEX]g\left(x \right)={x}^{3}-3x[/TEX]
Xét f(x), g(x) trên đoạn [0;1],
Ta có: [TEX]f'\left(x \right)=4{x}^{3}-3x[/TEX]
vẽ BBT ra, => Max f(x)=1, tại x=0; Min f(x)=-1,035....tại [TEX]x={\sqrt{3}}_{2}[/TEX]
Tương tự: [TEX]g'\left(x \right)=3{x}^{2}-1[/TEX]
vẽ BBT ra => [TEX]Maxg\left(x \right)=-1,539....[/TEX], g(x) không có GTNN trên [0;1]
vậy [TEX]Max \int_{0}^{1}\left({x}^{4}-3x+1;{x}^{3}-3 \right)dx[/TEX]
=Max f(x)+Max g(x)=1-1,539....=....
[TEX]Min \int_{0}^{1}\left({x}^{4}-3x+1;{x}^{3}-3 \right)dx[/TEX]=Min f(x)+Min g(x)=-1,035....

Tất cả nằm xuống, BOM B52 tới kìa.!!!!!!!!
images

images

MOD ơi xoá dùm em bài này, em làm sai mất tiu oyf, quên mất cách làm, chế tùm bậy
 
Last edited by a moderator:
K

kiburkid

Dạng tìm max min của tích phân cho vào sử sách lâu rồi
Nhưng một số sách vẫn có
Em vừa đọc một chút nó làm khác cơ.
Tính f(x)-g(x)=h(x) rồi xét cái hàm đó
Nhưng vấn đề em không hiểu 2 hàm trong tích phân thì có nghĩa là rì
Mà thôi kệ, có thi cái ni đâu quan tâm làm rì ...
 
L

lantrinh93

trời !!
ghê quá ,mình mở ra có 1 bài , mới có mấy giờ lên đến 4 trang
yeah!!
thế bà con giúp em bài này luôn nha
thanks
[TEX] I = \int_{1}^{2}\frac{dx}{x+2\sqrt{2x-x^2}-1}[/TEX]@};-@};-@};-:D;)
 
K

kenylklee

uhm, cũng có một kiểu như vậy, làm nãy giờ mình suy nghĩ đến trọc đầu, cố gắng pót cẩn thận nha, chưa ăn cơm nữa nè, đói muốn chết. À các Bác , mình có mọt số bài tập tích phân hay, ma theo nguyên văn Bác vivietnam là hơi bị kinh điển và đặc biệt, mời các bạn vào thử sức nha, thank.
http://diendan.hocmai.vn/showthread.php?t=148143
 
K

kiburkid

lantrinh93 said:
trời !!
ghê quá ,mình mở ra có 1 bài , mới có mấy giờ lên đến 4 trang
yeah!!
thế bà con giúp em bài này luôn nha
thanks
[TEX] I = \int_{1}^{2}\frac{dx}{x+2\sqrt{2x-x^2}-1}[/TEX]@};-@};-@};-:D;)
Bấm để xem đầy đủ nội dung ...


Hjx
Làm đến đây chả bjt làm rì nữa
[tex]\int\limits_{1}^{2}{\frac{2\sqrt{2x-x^2} }{{5x^2-10x+1}} {dx}[/tex]
 
A

acsimet_91

kiburkid said:
u = x
dv = ln(...)dx ---> v = (2x+1) / (x^2+x+1)
Tách ra làm 2x/(x^2+x+1) + 1/(x^2+x+1)
rồi làm như bình thường
Bấm để xem đầy đủ nội dung ...
Cậu thật là........ việc gì phải tách ra thế cho khổ mình? Như bà chị kia nói rồi đấy
ngoisaohieulongtoi92 said:
bình thường là như thế nào em?e giải ra kết quả đi;)).....em tách thế có mà tết pháp cũng k giải ra

chị giải tiếp cho chủ thớt dễ hiểu nhé

(2x+1)dx chính là d(x^2+x+1) đấy e ah:).vì đạo hàm của x^2+x+1 =2x+1:D.đến đây mới đc nói là dễ nhé:).đáp án là vế uv/- ln(x^2+x+1)/
em thế cận vào là xong:)
Bấm để xem đầy đủ nội dung ...
Bà chị giàu kinh nghiệm hơn người ta 1 chút nhưng ai bảo đến tết pháp cũng ko ra? =))
Nếu giải tiếp theo tư duy của bạn ấy thì cũng chỉ dài hơn vài dong thôi, làm chi mà cậy giọng chị cả, to còi dữ vậy? =))
Vậy em làm tiếp cho bà chị coi nhá (tất nhiên như em nói, cách này đúng là ko tối ưu = cách của bà chị nhưng ko phải là ko thể thực hiện được ;)) ) . Em viết nguyên hàm cho nhanh:
[TEX]I=\int_{}^{}\frac{2x}{x^2+x+1}dx+\int_{}^{}\frac{dx}{x^2+x+1}= \int_{}^{}\frac{2x}{(x+\frac{\sqrt{3}}{2})^2+ \frac{1}{4}}du+\int_{}^{}\frac{du}{(x+\frac{\sqrt{3}}{2})^2+ \frac{1}{4}}[/TEX]

đặt [TEX]x + \frac{\sqrt{3}}{2}=\frac{1}{2}tanu \Rightarrow dx = \frac{du}{2cos^2x}[/TEX]

[TEX]x=\frac{tanu}{2}-\frac{\sqrt{3}}{2}[/TEX]
[TEX]I= \int_{}^{}4( \frac{tanu}{2}-\frac{\sqrt{3}}{2})du +\int_{}^{}2du [/TEX]
=[TEX] \int_{}^{}\frac{2sinu}{cosu}du -\int_{}^{}(2-2\sqrt{3})du[/TEX]

Đến đây thì nói "làm như bình thường" được chưa ạ? =)). ko biết có tính nhầm ở đâu ko nhưng hướng làm thì như thế ;))
 
Last edited by a moderator:
N

ngoisaohieulongtoi92

acsimet_91 said:
Cậu thật là........ việc gì phải tách ra thế cho khổ mình? Như bà chị kia nói rồi đấy

Bà chị giàu kinh nghiệm hơn người ta 1 chút nhưng ai bảo đến tết pháp cũng ko ra? =))
Nếu giải tiếp theo tư duy của bạn ấy thì cũng chỉ dài hơn vài dong thôi, làm chi mà cậy giọng chị cả, to còi dữ vậy? =))
Vậy em làm tiếp cho bà chị coi nhá (tất nhiên như em nói, cách này đúng là ko tối ưu = cách của bà chị nhưng ko phải là ko thể thực hiện được ;)) ) . Em viết nguyên hàm cho nhanh:
[TEX]I=\int_{}^{}\frac{2x}{x^2+x+1}dx+\int_{}^{}\frac{dx}{x^2+x+1}= \int_{}^{}\frac{2x}{(x+\frac{\sqrt{3}}{2})^2+ \frac{1}{4}}du+\int_{}^{}\frac{du}{(x+\frac{\sqrt{3}}{2})^2+ \frac{1}{4}}[/TEX]

đặt [TEX]x + \frac{\sqrt{3}}{2}=\frac{1}{2}tanu \Rightarrow dx = \frac{du}{2cos^2x}[/TEX]

[TEX]x=\frac{tanu}{2}-\frac{\sqrt{3}}{2}[/TEX]
[TEX]I= \int_{}^{}4( \frac{tanu}{2}-\frac{\sqrt{3}}{2})du +\int_{}^{}2du [/TEX]
=[TEX] \int_{}^{}\frac{2sinu}{cosu}du -\int_{}^{}(2-2\sqrt{3})du[/TEX]

Đến đây thì nói "làm như bình thường" được chưa ạ? =)). ko biết có tính nhầm ở đâu ko nhưng hướng làm thì như thế ;))
Bấm để xem đầy đủ nội dung ...
sau 2 năm k học k xem sách,k nhớ đc dạng đặc biệt của dạng bình phương thiếu tách thành bình phương và cộng thêm 1 số bình phương nữa rồi đặt kiểu như c:)).nhưng dù sao cũng thanks,nếu giàu kinh nghiệm thế,sao k nhìn xem em ấy làm tích phân từng phần sai hay đúng:).t k để ý kỹ và giải tiếp tích phân e ấy,tí nữa mấy bạn chỉ chỗ sai chỗ từng phần ấy:)).k phải ngồi đấy xoắn:)).k đỡ đc=)) và giàu kinh nghiệm thì giải nốt bài đang cần giải ở trên đi:))
 
Last edited by a moderator:
A

acsimet_91

ngoisaohieulongtoi92 said:
sau 2 năm k học k xem sách,k nhớ đc dạng đặc biệt của dạng bình phương thiếu tách thành bình phương và cộng thêm 1 số bình phương nữa rồi đặt kiểu như c:)).nhưng dù sao cũng thanks,nếu giàu kinh nghiệm thế,sao k nhìn xem em ấy làm tích phân từng phần sai hay đúng:).t k để ý kỹ và giải tiếp tích phân e ấy,tí nữa mấy bạn chỉ chỗ sai chỗ từng phần ấy:)).k phải ngồi đấy xoắn:)).k đỡ đc=)) và giàu kinh nghiệm thì giải nốt bài đang cần giải ở trên đi:))
Bấm để xem đầy đủ nội dung ...

Làm chi mà cười dữ vậy chị? =))

Em làm được thì chị làm người yêu của em nhá =))
[TEX]\int_{1}^{2}\frac{dx}{x+2\sqrt{2x-x^2}-1}=\int_{1}^{2}\frac{x-1-2\sqrt{2x-x^2}}{5x^2-10x+1}dx=\int_{1}^{2}\frac{x-1}{5x^2-10x+1}dx-2\int_{1}^{2}\frac{\sqrt{2x-x^2}}{5x^2-10x+1}[/TEX]

[TEX]I_1=\int_{1}^{2}\frac{x-1}{5x^2-10x+1}dx[/TEX]

\Rightarrow Cái này xin miễn cho em phần tính toán nhá. ko tính được thì đập đầu vào gối mà chết đi =))

[TEX]I_2=\int_{1}^{2}\frac{\sqrt{2x-x^2}}{5x^2-10x+1}dx=\int_{1}^{2}\frac{\sqrt{1-(x-1)^2}}{5(x-1)^2-4}dx=\int_{0}^{1}\frac{\sqrt{1-u^2}}{5u^2-4}du[/TEX]

Đặt [TEX]u=sinv (v thuoc [0;\frac{\pi}{2}] ) [/TEX]

[TEX]\sqrt{1-u^2}=cosv; du=cosvdv[/TEX]. Viết nguyên hàm cho nhanh. tự đổi cận

[TEX]I_2=\int_{}^{}\frac{cos^2v}{5sin^2v-4}dv=\int_{}^{}\frac{1-sin^2v}{5sin^2v-4}dv[/TEX]

Đặt [TEX]t = tan\frac{v}{2} \Rightarrow dt=\frac{t^2+1}{2}dv [/TEX]

[TEX]sinv=\frac{2t}{t^2+1}\Rightarrow sin^2v=\frac{4t^2}{(t^2+1)^2}[/TEX]

Thay vào [TEX]I_2[/TEX]

[TEX]I_2=\frac{-1}{2}\int_{}^{}\frac{t^4-2t^2+1}{(t^2+1)(t^4-3t^2+1)}dt=\frac{-1}{2}\int_{}^{} \frac{t^4-2t^2+1}{(t^2+1)(t^2+t-1)(t^2-t-1)} = \int_{}^{}\frac{4dt}{5(t^2+1)}+\frac{1}{10}.\int_{}^{}\frac{2t-1}{t^2-t-1}dt-\frac{1}{10}\int_{}^{}\frac{2t+1}{t^2+t-1}[/TEX]

Dùng cách đồng nhất hệ số để tách thôi. Đến đây em ko tính nữa :D
Chị ơi làm bạn gái em đi =))
Bấm để xem đầy đủ nội dung ...
 
Last edited by a moderator:
A

acsimet_91

kiburkid said:
Làm sai còn bày đặt đi kua gái :p
........................................
Bấm để xem đầy đủ nội dung ...


acsimet_91 said:
Đặt [TEX]t = tan\frac{v}{2} \Rightarrow dt=\frac{t^2+1}{2}dv [/TEX]

Bấm để xem đầy đủ nội dung ...

Bài sai hay cậu ko đủ trình để hiểu? ;))

[TEX]t = tan\frac{v}{2} \Rightarrow dt=\frac{1}{2cos^2\frac{v}{2}}dv=\frac{1}{2}.(tan^2 \frac{v}{2}+1)dv=\frac{1}{2}.(t^2+1)dv[/TEX]

sai ở đâu vậy cậu? =)). ko nói được thì về làm vk bé của t đi =))

 
You must log in or register to reply here.
Top Bottom