[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1: Dấu của tam thức bậc 2
1. Tam thức bậc 2VD: [imath]f(x) = 2x^2 + 2x +1 ; g(x) = 2x^2 + 1; h(x) = x^2 + x ...[/imath]
Đa thức bậc hai [imath]f(x) = ax^2 + bx + c[/imath] với [imath]a;b;c[/imath] là các hệ số, [imath]a \ne 0[/imath] và [imath]x[/imath] là biến số gọi là tam thức bậc hai
Nhận xét: Cho tam thức bậc hai [imath]f(x) = ax^2 + bx + c (a \ne 0)[/imath]. Khi thay [imath]x[/imath] bằng giá trị [imath]x_o[/imath] vào [imath]f(x)[/imath] ta được: [imath]f(x_o) = ax_o^2 + bx_o + c[/imath], gọi là giá trị của tam thức bậc 2 tại [imath]x_o[/imath]
- Nếu [imath]f(x_o) > 0[/imath] thì ta nói [imath]f(x)[/imath] dương tại [imath]x_o[/imath]
- Nếu [imath]f(x_o) < 0[/imath] thì ta nói [imath]f(x)[/imath] âm tại [imath]x_o[/imath]
- Nếu [imath]f(x)[/imath] dương (âm) tại mọi điểm [imath]x[/imath] thuộc 1 khoảng hoặc 1 đoạn thì ta nói [imath]f(x)[/imath] dương(âm) trên khoảng đó
a) [imath]f(x) = 2x +1[/imath]
b) [imath]g(x) = x^2 + 3x + 2[/imath]
c) [imath]h(x) = x^2 + 1[/imath]
Đáp án: [imath]b;c[/imath] là các tam thức bậc 2. Câu a) không chứa [imath]x^2[/imath]
Cho tam thức bậc hai [imath]f(x) = ax^2 + bx + c (a \ne 0)[/imath]. Khi đó:
- Nghiệm của PT bậc hai [imath]ax^2 + bx+ c = 0[/imath] là nghiệm của [imath]f(x)[/imath]
- Biểu thức [imath]\Delta = b^2 -4ac[/imath] và [imath]\Delta' = \left (\dfrac{b}{2} \right)^2 - ac[/imath] lần lượt là biệt thức và biệt thức thu gọn của [imath]f(x)[/imath]
VD: Tìm biệt thức và nghiệm của tam thức bậc hai: [imath]f(x) = x^2 + 3x + 2[/imath]
Giải: [imath]\Delta = 3^2 - 4.2 = 1[/imath]
Do đó, nghiệm của PT là: [imath]x_1 = \dfrac{-3 + 1}{2} = -1 ; x_2 = \dfrac{-3 -1}{2} = -2[/imath]
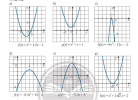
2. Định lí về dấu của tam thức bậc 2
Cho tam thức bậc hai [imath]f(x) = ax^2 + bx + c (a \ne 0)[/imath]. Khi đó:
- Nếu [imath]\Delta <0[/imath] thì [imath]f(x)[/imath] cùng dấu với [imath]x[/imath] với mọi [imath]x[/imath]
- Nếu [imath]\Delta = 0[/imath] và [imath]x_o = \dfrac{-b}{2a}[/imath] là nghiệm kép của [imath]f(x)[/imath] thì [imath]f(x)[/imath] cùng dấy với [imath]a[/imath] với mọi [imath]x \ne x_o[/imath]
- Nếu [imath]\Delta >0[/imath] và [imath]x_1;x_2[/imath] là 2 nghiệm của [imath]f(x) (x_1 <x_2)[/imath] thì [imath]f(x)[/imath] trái dấu với [imath]a[/imath] trong mọi [imath]x[/imath] trong khoảng [imath](x_1;x_2)[/imath]; [imath]f(x)[/imath] cùng dấu với [imath]a[/imath] trong mọi [imath]x[/imath] thuộc 2 khoảng [imath](-\infty; x_1); (x_2; +\infty)[/imath]
- B1: Tính và xác định dấu của [imath]\Delta[/imath]
- B2: Xác định nghiệm nếu có
- B3: Xác định dấu của hệ số [imath]a[/imath]
- B4: Xác định dấu của [imath]f(x)[/imath]
VD1: Xét dấu của tam thức bậc 2 sau: [imath]f(x) = x^2 + 5x + 4[/imath]
Lời giải:
[imath]\Delta = 5^2 - 4.4 = 9 > 0[/imath]
[imath]x_1 = -1; x_2 = -4 ; a = 1 >0[/imath]
Lập Bảng xét dấu:
| [imath]x[/imath] |
| |
| [imath]f(x)[/imath] | [imath]\ \ \ \ \ \ + \ \ \ \ \ \ \ \ \ 0 \ \ \ \ - \ \ \ \ \ \ \ 0 \ \ \ \ +[/imath] |
VD2: Xét dấu của tam thức bậc hai [imath]f(x) = x^2 + 2x + 1[/imath]
Lời giải:
[imath]\Delta = 2^2 - 4.1 = 0[/imath]
Nghiệm kép [imath]x_o = -1[/imath]
| [imath]x[/imath] |
| |||
| [imath]f(x)[/imath] | [imath]\ \ \ \ \ \ \ \ \ + \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ +[/imath] |
Last edited: