S
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
S
son_9f_ltv
B
bigbang195

câu cuối của đề thi thử Ams
Bài này giải như nào vậy cậu giúp mình với
S
son_9f_ltv
S
son_9f_ltv
S
son_9f_ltv
[TEX]min......A=\frac{(x+y)^4}{x^3}........................(x,y\in N*;x,y le?)[/TEX]
ko ai giả vậy mình giải nha!!
d là UCLN (x,y) thì x=da,y=db,(a,b)=1
ta có
[TEX](a,b)=1[/TEX]nên[TEX](a,a+b)=1[/TEX]do đó [TEX](a^3,(a+b)^4)=1[/TEX]|leftrightarrow [TEX]d\vdots a^3[/TEX]
giả sử [TEX]d=a^3c[/TEX](c nguyên dương.Khi đó A=c(a+b)^4 với a,b,c nguyên dương.
A lẻ suy ra c,a+b lẻ A min,ta chọn c=1,a+b=3 \Rightarrow A=81
a+b=3 \Rightarrow a=2,b=1 hoặc a=1,b=2
Vậy A min =81 khi x=16,y=8 hoặc x=1,y=2
P/S đây là 1 bài trong sách nâng cao-phát triển toán của Vũ Hữu Bình,lời giải của mình cũng là copy từ đó ra
S
son_9f_ltv
S
son_9f_ltv
K
khanh.kid
bài này trong dè nào quên mất rồitiếp bài nữa nha
x,y,z ko âm,x+y+z=1,tìm max
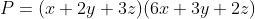
8P = 4(2x+4y+6z)(6x+3y+2z) \leq (8(x+y+z)-y)^2 \leq 64
=> P= \leq 8
=> P max=8 <=>x=z=0,5, y=0
hinh như là thé này
1 điều đặc biết j là nhiều bài trong đè thi các trường chuyên lấy trong sách
ai hên trước ngày thi gặp được thì ổn
S
son_9f_ltv
mọi ng` giúp hộ mình 1 bài nha
[TEX]a,b>0....a+b=1...CM \frac{2}{ab}+\frac{3}{a^2+b^2}\ge 14[/TEX]
P/S thằng bạn nó gợi ý rồi nhwng mình chwa có time để nghĩ nên nhờ mọi ng` chém hộ!!thanks !!!
[TEX]a,b>0....a+b=1...CM \frac{2}{ab}+\frac{3}{a^2+b^2}\ge 14[/TEX]
P/S thằng bạn nó gợi ý rồi nhwng mình chwa có time để nghĩ nên nhờ mọi ng` chém hộ!!thanks !!!
M
m_k80
D
duynhan1
mọi ng` giúp hộ mình 1 bài nha
[TEX]a,b>0....a+b=1...CM P=\frac{2}{ab}+\frac{3}{a^2+b^2}\ge 14[/TEX]
[TEX](a+b)^2 \geq 4ab[/TEX]
[TEX]ab \leq \frac14[/TEX]
[TEX]P=\frac{2}{ab}+\frac{3}{a^2+b^2} = \frac{1}{2ab} + 3(\frac{1}{2ab} + \frac{1}{a^2+b^2}) \geq 2+ 3(\frac{4}{(a+b)^2}) \geq 14[/TEX]
V
vodichhocmai
mọi ng` giúp hộ mình 1 bài nha
[TEX]a,b>0....a+b=1...CM \frac{2}{ab}+\frac{3}{a^2+b^2}\ge 14[/TEX]
P/S thằng bạn nó gợi ý rồi nhwng mình chwa có time để nghĩ nên nhờ mọi ng` chém hộ!!thanks !!!
[TEX]\frac{4}{2ab}+\frac{4}{a^2+b^2}-\frac{1}{a^2+b^2} \ge \frac{16}{(a+b\)^2}- \frac{2}{(a+b\)^2}[/TEX]
V
vanconuong
V
vnzoomvodoi
câu cuối đề thi thử Ams thực chất đã xuất hiện trong đề thi thật một lần rồi (mình 0 nhớ rõ, bạn thử tìm xem), nhưng có điều ở dạng khác
M
m_k80
Mình không hiểu
Bài giải của anh vodichhocmai là 1 bài dạng khác . Bài cuối đề thi thử Ams dạng khác .
Bài giải của anh vodichhocmai là 1 bài dạng khác . Bài cuối đề thi thử Ams dạng khác .
B
big.bang
S
son_9f_ltv
theo mình topic này là dành cho cả người k thi chuyên nên đừng có sử dụng bdt schwarz ...
đó là 1 BĐT quen thuộc,khá phổ biến mà bạn
S
son_9f_ltv
thi xong oy ,quay trở ại bt thôi mọi ng`
[TEX]a\ge 2,b\ge 6,c\ge 12......max \frac{bc\sqrt{a-2}+ca\sqrt[3]{b-6}+ab\sqrt[4]{c-12}}{abc}[/TEX]
[TEX]a\ge 2,b\ge 6,c\ge 12......max \frac{bc\sqrt{a-2}+ca\sqrt[3]{b-6}+ab\sqrt[4]{c-12}}{abc}[/TEX]
S
son_9f_ltv
Hi Lạp MO 2007
[TEX]\sum{\frac{(a+c-b)^4}{a(a+b-c)}}\ge \sum{ab}[/TEX]
với a,b,c là các cạnh của tam giác
[TEX]\sum{\frac{(a+c-b)^4}{a(a+b-c)}}\ge \sum{ab}[/TEX]
với a,b,c là các cạnh của tam giác

