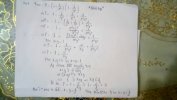[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1: Chứng minh bât đẳng thức:
a) [imath]x^{2}+\dfrac{1}{x} \geq 2[/imath]
b) [imath]a^{2}+b^{2}+c^{2} \geq a b+b c+c a[/imath]
c) [imath](a+b)\left(\dfrac{1}{a}+\dfrac{1}{b}\right) \geq 4[/imath] với [imath]\mathrm{a}, \mathrm{b}>0[/imath]
d) [imath](a+1)(b+1)(c+1) \geq 8[/imath] với [imath]\mathrm{a}, \mathrm{b}, \mathrm{c}>0[/imath] và [imath]a b c=1[/imath].
Bài 2: Cho [imath]x, y>0, x+y=1[/imath]. Tìm GTNN của [imath]\mathrm{P}=\left(1-\dfrac{1}{x^{2}}\right)\left(1-\dfrac{1}{y^{2}}\right)[/imath].
Bài 3: Cho [imath]x>0, y>0[/imath] thỏa mãn [imath]x+y \leq 1[/imath]. Tìm GTNN của [imath]P=\dfrac{1}{x^{2}+y^{2}}+\dfrac{2}{x y}+4 x y[/imath].
Em có một số bài toán nâng cao. Mong mọi người giúp em. Em cảm ơn
a) [imath]x^{2}+\dfrac{1}{x} \geq 2[/imath]
b) [imath]a^{2}+b^{2}+c^{2} \geq a b+b c+c a[/imath]
c) [imath](a+b)\left(\dfrac{1}{a}+\dfrac{1}{b}\right) \geq 4[/imath] với [imath]\mathrm{a}, \mathrm{b}>0[/imath]
d) [imath](a+1)(b+1)(c+1) \geq 8[/imath] với [imath]\mathrm{a}, \mathrm{b}, \mathrm{c}>0[/imath] và [imath]a b c=1[/imath].
Bài 2: Cho [imath]x, y>0, x+y=1[/imath]. Tìm GTNN của [imath]\mathrm{P}=\left(1-\dfrac{1}{x^{2}}\right)\left(1-\dfrac{1}{y^{2}}\right)[/imath].
Bài 3: Cho [imath]x>0, y>0[/imath] thỏa mãn [imath]x+y \leq 1[/imath]. Tìm GTNN của [imath]P=\dfrac{1}{x^{2}+y^{2}}+\dfrac{2}{x y}+4 x y[/imath].
Em có một số bài toán nâng cao. Mong mọi người giúp em. Em cảm ơn
Attachments
Last edited by a moderator: