[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào tất cả các bạn 
Phần Vecto là phần đầu của hình học lớp 10, các bạn lần đầu tiên tiếp cận với một kiến thức mới nên còn nhiều bỡ ngỡ. Vì vậy hôm nay, mình đưa đến cho các bạn Chuyên đề Vecto để các bạn có thể tìm hiểu rõ hơn về dạng bài này. Mong các bạn ủng hộ mình, nhớ tag bạn bè vào xem luôn nha.
I) Nhắc lại kiến thức:
1. Khái niệm:
[tex]\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{OB}+\overrightarrow{AO}[/tex] (phép trừ)
Phần Vecto là phần đầu của hình học lớp 10, các bạn lần đầu tiên tiếp cận với một kiến thức mới nên còn nhiều bỡ ngỡ. Vì vậy hôm nay, mình đưa đến cho các bạn Chuyên đề Vecto để các bạn có thể tìm hiểu rõ hơn về dạng bài này. Mong các bạn ủng hộ mình, nhớ tag bạn bè vào xem luôn nha.
I) Nhắc lại kiến thức:
1. Khái niệm:
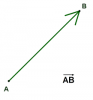
- Vecto là một đoạn thẳng có hướng, nghĩa là đã chỉ rõ điểm điểm mút nào là điểm đầu, điểm mút nào là điểm cuối. Được đặc trưng bởi các yếu tố: Phương, Hướng( chiều), Độ dài.
- Hướng từ điểm đầu đến điểm cuối của vectơ được gọi là hướng của vectơ.
- Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau.
- Hai vectơ bằng nhau nếu như chúng có cùng hướng và cùng độ dài.
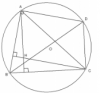
- Quy tắc 3 điểm: Cho 3 điểm A, B, O bất kỳ, ta có:
[tex]\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{OB}+\overrightarrow{AO}[/tex] (phép trừ)
- Các tính chất như giao hoán, kết hợp, cộng với [tex]\overrightarrow{0}[/tex] giống như trong số học.
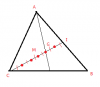
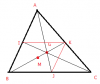
- Nếu M là trung điểm của đoạn thẳng AB, I là 1 điểm bất kỳ ta có hệ thức sau: [tex]\overrightarrow{IM}=\frac{\overrightarrow{IA}+\overrightarrow{IB}}{2}[/tex]
- Nếu G là trọng tâm tam giác ABC ta có: [tex]\overrightarrow{IG}=\frac{\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}}{3}[/tex] và [tex]\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}[/tex]
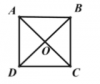
- ABCD là hình bình hành ta được: [tex]\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}[/tex]