L
l94
1.
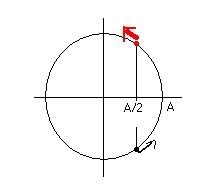
[TEX]\Rightarrow 20 \pi t + \frac{3\pi}{4} = \frac{5\pi}{6} + k 2\pi[/TEX]( với k=0,1,2...)
k=0 ứng với lần 1.
k=10 ứng với lần 11 [TEX]\Rightarrow t = 1,004(s)[/TEX]
2.
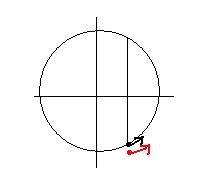
Mỗi chu kỳ đi qua vị trí đó 1 lần theo chiều âm. trong chu kỳ thứ 5 suy ra lần thứ 5 ứng với k=4.
[TEX]t = 0,204 (s)[/TEX]
câu 2 cậu nhằm chỗ nào rồi thì phải
thời gian vật qua lần đầu là
[TEX]t=\frac{1}{240}[/TEX]
nên thời gian mà vật qua vị trí đó trong chu kỳ thứ 5 phải là
[TEX]t'=\frac{1}{240} + 0,1.4=0,404[/TEX]