H
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- Status
- Không mở trả lời sau này.
D
duynhan1
Định hướng: Nhận thấy ở phương trình (2) có x^2y nên ta nhân thêm y ở 1 để đặt ẩn phụ..Bài 53:
[TEX]\left{\begin{ x^2(y+1)=6y-2 \\ x^4y^2 + 2x^2y^2 + y(x^2+1)=12y^2-1[/TEX]
Bài giải:
Với [TEX]y=0[/TEX], ta có hệ phương trình đã cho vô nghiệm.
Với [TEX]y \not= 0 [/TEX], hệ đã cho tương đương với:
[TEX]\left{ x^2y(y+1) = 6y^2 - 2y \\ (x^2y)^2 + 2x^2y.y + x^2y + y = 12y^2 - 1[/TEX]
Đặt [TEX]\left{ a = x^2 y \\ b = y [/TEX], ta có:
[TEX]\left{ a (b+1) = 6b^2 - 2b \\ a^2 + 2ab + a + b = 12b^2 - 1 \right. \\ \Leftrightarrow \left{ a = \frac{6b^2 - 2b}{b+1} (do\ b=-1\ thi\ he\ vo\ nghiem) \\ (a+b-3)(a+b+4) = 13(b^2-1)[/TEX].
Thay (1) và (2) ta có:
[TEX]\frac{6b^2 - 2b + b^2 + b - 3b - 3 }{b+1} \ . \ \frac{6b^2 -2b + b^2 + b + 4b + 4}{b+1} = 13(b^2-1) \\ \Leftrightarrow \frac{( b - 1)( 7b + 3)( 7b^2 + 3b + 4) }{(b+1)^2}= 13(b-1)(b+1) \\ \Leftrightarrow \left[ b = 1 \\ 49b^3 + 42b^2 + 37b + 12 = 13 ( b^3 + 3b^2 + 3b+1) \right. \\ \Leftrightarrow \left[ b = 1 \\ 36b^3 + 3b^2 - 2b - 1 = 0 \right. \\ \Leftrightarrow \left[ b = 1 \\ b = \frac13 [/TEX]
- [TEX]b= 1 \Rightarrow a = 2 \Rightarrow \left{ x = \pm \sqrt{2} \\ y = 1[/TEX]
- [TEX]b = \frac13 \Rightarrow a= 0 \Rightarrow \left{ x = 0 \\ y = \frac13[/TEX]
[TEX]\left[ \left{ x = \pm \sqrt{2} \\ y = 1\right. \\ \left{ x = 0 \\ y = \frac13 \right.[/TEX]
L
langtu_117
Điều kiện: [TEX]|x|<\frac{1}{2}[/TEX]Bài 55: Giải phương trình:
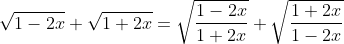
Theo Cô-Si, ta có dãy BĐT sau:
[TEX]1.\sqrt{1-2x}\leq \frac{(1-2x)+1}{2} \ \ (1)[/TEX]
[TEX]1.\sqrt{1+2x}\leq \frac{(1+2x)+1}{2} \ \ (2)[/TEX]
[TEX]\sqrt{\frac{1-2x}{1+2x}}+\sqrt{\frac{1+2x}{1-2x}}\geq 2\sqrt{\sqrt{\frac{1-2x}{1+2x}}.\sqrt{\frac{1+2x}{1-2x}}}=2 \ \ (3)[/TEX]
Lấy [TEX](1)+(2)[/TEX], ta được:
[TEX]VT=\sqrt{1-2x}+\sqrt{1+2x}\leq 2[/TEX]
Từ [TEX](3)[/TEX], suy ra:
[TEX]VP\geq 2[/TEX]
Suy ra:
[TEX]VT=VP\Leftrightarrow \left\{\begin{matrix}VT=2\\VP=2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\sqrt{1-2x}=1\\ \sqrt{1+2x}=1\\ \sqrt{\frac{1+2x}{1-2x}}=\sqrt{\frac{1-2x}{1+2x}}\end{matrix}\right.\Leftrightarrow x=0[/TEX]
Kết hợp với điều kiện suy ra phương trình có 1 nghiệm là : [TEX]x=0[/TEX]
Last edited by a moderator:
P
peto_cn94
Bài 56:giải hệ:
[TEX]\left{\begin{y+2=(3-x)^2}\\{(2z-y)(y+2)=9+4y}\\{x^2+z^2=4x}\\{z\geq0[/TEX]
[TEX]\left{\begin{y+2=(3-x)^2}\\{(2z-y)(y+2)=9+4y}\\{x^2+z^2=4x}\\{z\geq0[/TEX]
Last edited by a moderator:
S
stork_pro
Bài 57
[TEX]\left{\begin{2(2x+1)^3+2x+1=(2y-3)\sqrt{y-2}}\\{\sqrt{4x+2}+\sqrt{2y+4}=6[/TEX]
Bài 58
[TEX]\left{\begin{y^3+y=x^3+3x^2+4x+2}\\{\sqrt{1-x^2}-\sqrt{2-y}-1}=0[/TEX]
[TEX]\left{\begin{2(2x+1)^3+2x+1=(2y-3)\sqrt{y-2}}\\{\sqrt{4x+2}+\sqrt{2y+4}=6[/TEX]
Bài 58
[TEX]\left{\begin{y^3+y=x^3+3x^2+4x+2}\\{\sqrt{1-x^2}-\sqrt{2-y}-1}=0[/TEX]
Last edited by a moderator:
N
nhocngo976
[TEX](1) \leftrightarrow y^3+y= (x+1)^3+(x+1)[/TEX]Bài 58
[TEX]\left{\begin{y^3+y=x^3+3x^2+4x+2}\\{\sqrt{1-x^2}-\sqrt{2-y}-1}[/TEX]
xét [TEX]f(t)= t^3 +t \\\\ f'(t)= 3t^2+1 >0 \ voi \ moi \ t\ \\\\ \rightarrow f(t) \ DB \rightarrow y=x+1[/TEX]
thế vào (2), ta có:
[TEX](2) \leftrightarrow \sqrt{1-x^2}= \sqrt{1-x}+1 \\\\ (binh \ phuong ) \\\\ \leftrightarrow 2\sqrt{1-x}= -x^2+x-1 (VN) \ do \ -x^2 +x-1 <0 \ voi \ moi \ x [/TEX]
vậy hệ VN
Last edited by a moderator:
X
xlovemathx
Bài 59 : [TEX]\left\{ x^3+y^2=2 \\ x^2+xy+y^2-y=0 [/TEX]
Bài 60 : [TEX]\left\{ x^2+3y=9 \\ y^4+4(2x-3)y^2-48y-48x+155=0[/TEX]
Bài 61 : [TEX]\left\{ x^2y^2-2x+y^2=0 \\ 2x^3+3x^2+6y-12x+13=0[/TEX]
Bài 60 : [TEX]\left\{ x^2+3y=9 \\ y^4+4(2x-3)y^2-48y-48x+155=0[/TEX]
Bài 61 : [TEX]\left\{ x^2y^2-2x+y^2=0 \\ 2x^3+3x^2+6y-12x+13=0[/TEX]
D
duynhan1
Định hướng: Phương trình (1) và (2) rõ ràng không liên quan với nhau nên ta sẽ đánh giá để chứng tỏ hệ vô nghiệm.Bài 59 : [TEX]\left\{ x^3+y^2=2 (1)\\ x^2+xy+y^2-y=0(2) [/TEX]
Bài giải:
Xem phương trình (2) là phương trình bậc hai ẩn x, ta có:
[TEX]\Delta_x = y^2 - 4(y^2-y) = y( 4- 3y) \ge 0 \Rightarrow 0 \le y \le \frac43[/TEX]
Xem phương trình (2) là phương trình bậc hai ẩn y, ta có:
[TEX]\Delta_x = (x-1)^2 - 4x^2 = (-x -1)( 3x-1) \ge 0 \Rightarrow -1 \le x \le \frac13 [/TEX]
Do đó:
[TEX]x^3 + y^2 \le \frac{1}{27} + \frac{16}{9} = \frac{49}{27} <2 [/TEX]
Vậy hệ phương trình đã cho vô nghiệm.
Định hướng: Đề cho quan hệ giữa y và x^2 trong phương trình (1) phải chăng là để khử y trong phương trình (2) rồi xem phương trình (2) là ẩn y^2, thử thay y bởi x^2 xem sao.
Bài 60 : [TEX]\left\{ x^2+3y=9 \\ y^4+4(2x-3)y^2-48y-48x+155=0\right. [/TEX]
Bài giải:
Từ hệ ta suy ra:
[TEX]y^4 + 4(2x-3) y^2 - 16(9-x^2) - 48x + 155 = 0 \\ \Leftrightarrow y^4 + 4(2x-3)y^2 + 16x^2 - 48 x + 11 = 0(3) [/TEX]
Xem đây là phương trình bậc 2, ẩn [TEX]y^2[/TEX] ta có:
[TEX]\Delta = 4(2x-3)^2 - ( 16x^2 - 48x + 11) = 25[/TEX]
[TEX](3) \Leftrightarrow \left[ y^2 = -2(2x -3) - 5 = -4x + 1 \\ y^2 = -2(2x-3) + 5= - 4x + 11 [/TEX]
Trường hợp 1: [TEX]y^2 = 1- 4x [/TEX], ta có:
Thay vào (1) ta có:
[TEX](1-y^2)^2 + 48y = 144 \\ \Leftrightarrow y^4 = 2y^2 - 48y + 144 \\ \Leftrightarrow (y^2+1)^2 = (2y - 12)^2 \\ \Leftrightarrow \left[ y^2 +1 = 2y - 12(vo\ nghiem)\\ y^2 + 1 = 12 - 2y \right. \Leftrightarrow y = -1 \pm 2\sqrt{3} [/TEX]
Suy ra: [TEX]x = \frac{1-y^2}{4} = \frac{-3 \pm 2\sqrt{3}}{2}[/TEX]
Trường hợp 2: [TEX]y^2= 11- 4x [/TEX]
Thay vào (1) ta có:
[TEX]( 11- y^2)^2 + 48y = 144 \\ \Leftrightarrow y^4 = 22y^2 - 48 y + 23 \\ \Leftrightarrow (y^2 -5)^2 = 12(y-2)^2 \\ \Leftrightarrow \left[ y^2 - 5 = 2\sqrt{3} y - 4 \sqrt{3} \\ y^2 - 5 = -2\sqrt{3} y + 4\sqrt{3} \right. \Leftrightarrow \left[ y = \sqrt{3} \pm \sqrt{8-4\sqrt{3}} \\ y = -\sqrt{3} \pm \sqrt{8+ 4\sqrt{3}} \right. [/TEX]
Suy ra: [TEX]x=\frac{11-y^2}{4} [/TEX]
Kết luận:
Nghiệm xấu quá!
Định hướng: Nhận thấy từ phương trình (1) ta có: [TEX]{-1\le y= \frac{2x}{x^2+1} \le 1 [/TEX]. Do đó ta sẽ đánh giá từng phương trình để rút ra 1 cái gì đó.Bài 61 : [TEX]\left\{ x^2y^2-2x+y^2=0 (1) \\ 2x^3+3x^2+6y-12x+13=0(2)[/TEX]
Bài giải:
Từ phương trình (1) ta có:
[TEX]y^2 = \frac{2x}{x^2+1} [/TEX]
Mặt khác theo BĐT Cô-si ta có:
[TEX]x^2 + 1 \ge 2|x| \Rightarrow \frac{2x}{x^2+1} \le 1 \Rightarrow y^2 \le 1 \Leftrightarrow -1 \le y \le 1 (3) [/TEX]
và do [TEX]y^2 \ge 0 \Rightarrow x \ge 0 [/TEX]
Từ phương trình (2) ta có:
[TEX]{-6y = 2x^3 + 3x^2 - 12x + 13 [/TEX]
Xét hàm [TEX]f(x) = 2x^3 + 3x^2 - 12 x + 13 \forall x \ge 0[/TEX]
[TEX]f'(x) =6 x^2 + 6x - 12 \\ f'(x) = 0 \Leftrightarrow \left[ x= 1 \\ x=-2(loai)[/TEX]
[TEX]\circ \ f(1) = 6 \\ \circ f(0) = 13 \\ \circ \lim_{x \to + \infty} = + \infty[/TEX]
Do đó ta có: [TEX]f(x) \ge f(1) = 6 \forall x \ge 0[/TEX].[TEX]\Rightarrow -6y \ge 6 \Leftrightarrow y \le -1 (4) [/TEX]
Từ (3) và (4) suy ra [TEX]y=-1[/TEX]
[TEX]\Rightarrow x = 1[/TEX]
Kết luận: Nghiệm của hệ phương trình đã cho là :
[TEX]\left{ x =1 \\ y = -1[/TEX]
Last edited by a moderator:
L
langtu_117
Bài 62: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^3(2+3y)=1\\ x(y^3-2)=3\end{matrix}\right.[/TEX]
Bài 63: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^2+y^2-3x+4y=1\\ 3x^2-2y^2-9x-8y=3\end{matrix}\right.[/TEX]
Bài 64: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x\sqrt{x}-\sqrt{x}=y\sqrt{y}+8\sqrt{y}\\ x-y=5\end{matrix}\right.[/TEX]
Bài 65: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}y+xy^2=6x^2\\ 1+x^2y^2=5x^2\end{matrix}\right.[/TEX]
[TEX]\left\{\begin{matrix}x^3(2+3y)=1\\ x(y^3-2)=3\end{matrix}\right.[/TEX]
Bài 63: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^2+y^2-3x+4y=1\\ 3x^2-2y^2-9x-8y=3\end{matrix}\right.[/TEX]
Bài 64: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x\sqrt{x}-\sqrt{x}=y\sqrt{y}+8\sqrt{y}\\ x-y=5\end{matrix}\right.[/TEX]
Bài 65: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}y+xy^2=6x^2\\ 1+x^2y^2=5x^2\end{matrix}\right.[/TEX]
Post bài lên nào !!!
Last edited by a moderator:
D
destinyx4
Định hướngBài 65: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}y+xy^2=6x^2\\ 1+x^2y^2=5x^2\end{matrix}\right.[/TEX]
Cách giải:
Nhận thấy x,y=0 không phải là nghiệm của phương trình=>Thoải mái chia cho x và y
Ta chia cả 2 vế của cả 2 phương trình cho y^2 ta được:
[tex]\left\{ \frac{1}{y}+x=\frac{6x^2}{y^2} (1) \\ \frac{1}{y^2}+x^2=\frac{5x^2}{y^2}(2).[/TEX]
Mà
[TEX]\frac{1}{y^2}+x^2=(\frac{1}{y}+x)^2-2\frac{x}{y}.[/TEX]
Thế (1) vào (2) ta được:
[TEX]36\frac{x^4}{y^4}-5\frac{x^2}{y^2}-2\frac{x}{y}=0[/TEX]
[TEX]\rightarrow\frac{x}{y}=\frac{1}{2}=>x=2y[/TEX]
Thay vào phương trình đầu ta được
[TEX]4x^3-6x^2+2x=0[/TEX]
Do x=0 không phải là nghiệm nên:
[tex]4x^2-6x+2=0.[/tex]
[tex]\rightarrow \left\{ \begin{array}{l} x=1 \rightarrow y=2 \\ x=\frac{1}{2}\rightarrow y=1 \end{array} \right.[/tex]
Kết luận:Vậy nghiệm của phương trình là (x;y)=(1;2),(1/2;1)
Last edited by a moderator:
D
destinyx4
Bài 63: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^2+y^2-3x+4y=1\\ 3x^2-2y^2-9x-8y=3\end{matrix}\right.[/TEX]
Định hướng:Để ý nếu phương trình (1) nhân thêm với 3 thì sẽ xuất hiện rất nhiều cái giống với phương trình (2).Ta sẽ tiến hành nhân chéo 2 vế của phương trình với nhau
Bài Làm: Nhân chéo 2 vế của 2 phương trình với nhau ta được
[tex]3x^2+3y^2-9x+12y=3x^2-2y^2-9x-8y[/tex]
\Rightarrow 5y^2+20y=0
[tex]\Rightarrow\left\{ \begin{array}{l} y=0 \\ y =-4 \end{array} \right.[/tex]
Với y=0 ta có:
[tex]x^2-3x-1=0[/tex]
[tex]\Rightarrow\left\{ \begin{array}{l} x= \frac{3+\sqrt{13}}{2} \\ x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
Với y=-4 ta có
[tex]x^2-3x-1=0 [/tex]
[tex]\Rightarrow\left\{ \begin{array}{l} x= \frac{3+\sqrt{13}}{2} \\ x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
Vậy hệ phương trình có 4 cặp nghiệm
[tex]\left\{ \begin{array}{l} y=0;x= \frac{3+\sqrt{13}}{2} \\ y=0; x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
[tex]\left\{ \begin{array}{l}y=-4; x= \frac{3+\sqrt{13}}{2} \\ y=-4; x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
[TEX]\left\{\begin{matrix}x^2+y^2-3x+4y=1\\ 3x^2-2y^2-9x-8y=3\end{matrix}\right.[/TEX]
Định hướng:Để ý nếu phương trình (1) nhân thêm với 3 thì sẽ xuất hiện rất nhiều cái giống với phương trình (2).Ta sẽ tiến hành nhân chéo 2 vế của phương trình với nhau
Bài Làm: Nhân chéo 2 vế của 2 phương trình với nhau ta được
[tex]3x^2+3y^2-9x+12y=3x^2-2y^2-9x-8y[/tex]
\Rightarrow 5y^2+20y=0
[tex]\Rightarrow\left\{ \begin{array}{l} y=0 \\ y =-4 \end{array} \right.[/tex]
Với y=0 ta có:
[tex]x^2-3x-1=0[/tex]
[tex]\Rightarrow\left\{ \begin{array}{l} x= \frac{3+\sqrt{13}}{2} \\ x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
Với y=-4 ta có
[tex]x^2-3x-1=0 [/tex]
[tex]\Rightarrow\left\{ \begin{array}{l} x= \frac{3+\sqrt{13}}{2} \\ x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
Vậy hệ phương trình có 4 cặp nghiệm
[tex]\left\{ \begin{array}{l} y=0;x= \frac{3+\sqrt{13}}{2} \\ y=0; x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
[tex]\left\{ \begin{array}{l}y=-4; x= \frac{3+\sqrt{13}}{2} \\ y=-4; x= \frac{3-\sqrt{13}}{2}\end{array} \right.[/tex]
Last edited by a moderator:
D
destinyx4
Định hướng:Bài này phải sử dụng đến phương pháp hàm,không thì làm quá phức tạpBài 62: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^3(2+3y)=1(1)\\ x(y^3-2)=3(2)\end{matrix}\right.[/TEX]
Giải:
Từ phương trình (1) và (2) ta có:
[tex]\left\{ \begin{array}{l} \frac{1}{x^3}=2+3y \\ \frac{3}{x}=y^3-2 \end{array} \right.[/tex]
Cộng vế với vế:
[tex]\frac{1}{x^3}+\frac{3}{x}=y^3+3y.[/tex]
Xét hàm số t^3+3t
f(t)'=3t^2+3>0.Nên hàm số luôn đống biến
[tex]\Rightarrow\frac{1}{x}=y.[/tex]
Thay vào phương trình (1) ta được
[tex]x^3(2+\frac{3}{x})=1.[/tex]
[tex]\Rightarrow2x^3+3x^2-1=0.[/tex]
[tex]\Rightarrow\left\{ \begin{array}{l} x = -1\Rightarrow y=-1 \\ x= \frac{1}{2}\Rightarrow y=2\end{array} \right.[/tex]
Vậy hệ phương trình có nghiệm:
[tex]\Rightarrow\left\{ \begin{array}{l} x = -1; y=-1 \\ x= \frac{1}{2}; y=2\end{array} \right.[/tex]
Last edited by a moderator:
D
destinyx4
Định hướng:Bài này dồn căn về 1 bên và dồn những biểu thức không chứa căn về một bên:Bài 64: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x\sqrt{x}-\sqrt{x}=y\sqrt{y}+8\sqrt{y}\\ x-y=5\end{matrix}\right[/TEX]
Bài giải:
Từ 2 phương trình đầu ta dễ dàng có được:
[TEX]\frac{\sqrt{x}}{\sqrt{y}}=\frac{y+8}{x-1}[/TEX]
Do x-y=5=>x=y+5 thay vào phương trình trên rồi bình phương 2 vế ta được
[TEX]\frac{x}{y}=(\frac{x+3}{x-1})^2[/TEX]
Nhân chéo
=>[TEX]x(x-1)^2=(x-5)(x+3)^2[/TEX]
=>x=9 v x= -5/3
Với x=9=>y=4
Với x=-5/3=>y=-17/3.
Vậy phương trình có 2 cặp nghiệm
(x;y)=(9;4);(-5/3;-17/3)
Last edited by a moderator:
L
langtu_117
Bài 66: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}y=-x^3+3x+4\\ x=2y^3-6y-2\end{matrix}\right.[/TEX]
Bài 67: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x+\sqrt{1-y^2}=1\\ y+\sqrt{1-x^2}=\sqrt{3}\end{matrix}\right.[/TEX]
Bài 68: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}(x+\sqrt{x^2+1})(y+\sqrt{y^2+1})=1\\ y+\frac{y}{\sqrt{x^2-1}}+\frac{35}{12}=0\end{matrix}\right.[/TEX]
Bài 69: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^2+y^2=1\\ 125y^5-125y^3+6\sqrt{15}=0\end{matrix}\right.[/TEX]
Bài 70: Giải hệ phương trình: ( Dự bị 2 Khối B 2007)
[TEX]\left\{\begin{matrix}x+\frac{2xy}{\sqrt[3]{x^2-2x+9}}=x^2+y\\ y+\frac{2xy}{\sqrt[3]{y^2-2y+9}}=y^2+x\end{matrix}\right.[/TEX]
[TEX]\left\{\begin{matrix}y=-x^3+3x+4\\ x=2y^3-6y-2\end{matrix}\right.[/TEX]
Bài 67: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x+\sqrt{1-y^2}=1\\ y+\sqrt{1-x^2}=\sqrt{3}\end{matrix}\right.[/TEX]
Bài 68: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}(x+\sqrt{x^2+1})(y+\sqrt{y^2+1})=1\\ y+\frac{y}{\sqrt{x^2-1}}+\frac{35}{12}=0\end{matrix}\right.[/TEX]
Bài 69: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^2+y^2=1\\ 125y^5-125y^3+6\sqrt{15}=0\end{matrix}\right.[/TEX]
Bài 70: Giải hệ phương trình: ( Dự bị 2 Khối B 2007)
[TEX]\left\{\begin{matrix}x+\frac{2xy}{\sqrt[3]{x^2-2x+9}}=x^2+y\\ y+\frac{2xy}{\sqrt[3]{y^2-2y+9}}=y^2+x\end{matrix}\right.[/TEX]
Last edited by a moderator:
D
duynhan1
Định hướng: Nhận thấy ở phương trình (2) nhóm nhân tử được, và sau khi nhóm ngó lên 1 thì có thể thế được. Ở pt(1) là tổng, ở pt(2) là tích nên cố gắng tìm cách áp dụng Co-si thử xem sao.Bài 69: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x^2+y^2=1\\ 125y^5-125y^3+6\sqrt{15}=0\end{matrix}\right.[/TEX]
Bài giải:
[TEX](2) \Leftrightarrow 125x^2y^3 = 6 \sqrt{15}(3)[/TEX]
Từ phương trình (1) ta có:
[TEX]1= \frac{x^2}{2} + \frac{x^2}{2} + \frac{y^2}{3} + \frac{y^2}{3} + \frac{y^2}{3} \ge 5 \sqrt[5]{\frac{x^4y^6}{4.27}} \\ \Rightarrow 25\sqrt{5}|x^2y^3| \le 6\sqrt{3} \\ \Leftrightarrow 125|x^2y^3| \le 6\sqrt{15} \Rightarrow 125x^3y^2 \le (4) [/TEX]
Từ (3) và (4) suy ra [TEX]6 \sqrt{15} = 125x^2y^3 \le {6\sqrt{15}[/TEX]
Dấu "=" xảy ra khi và chỉ khi:
[TEX]\left{ \frac{x^2}{2} = \frac{y^2}{3} \\ x^2 + y^2 = 1 \\ x2y^3 \ge 0 \right. \Leftrightarrow \left{ x^2 = \frac25 \\ y^2 = \frac35 \\ x^2y^3 \ge 0 \right. \\ \Leftrightarrow \left{ x = \pm \sqrt{\frac25} \\ y = \sqrt{\frac35}[/TEX]
Thử lại 2 nghiệm trên là nghiệm của hệ phương trình.
Last edited by a moderator:
D
duynhan1
Định hướng: Khi không đưa được về đồng bậc , gặp 1 bên bậc 3, 1 bên bậc nhất, ta nhẩm nghiệm, phân tích rồi nhân chéo như sau.Bài 66: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}y=-x^3+3x+4\\ x=2y^3-6y-2\end{matrix}\right.[/TEX]
Bài giải:
Hệ phương trình đã cho tương đương với:
[TEX]\left{ y-2 = ( 2-x)(x+1)^2 \\ x-2 = 2(y-2)(y+1)^2[/TEX]
[TEX]\Rightarrow (x-2)(y-2) = 2(2-x)(y-2)(x+1)^2(y+1)^2 \\ \Leftrightarrow \left[ x=2 \\ y=2 [/TEX]
Trường hợp 1: x=2, thay vào hệ ban đầu ta có:
[TEX]\left{ y = 2 \\ 2y^3 - 6y - 2 = 2 \right. \Leftrightarrow y=2 \Rightarrow\left{ x=2 \\ y=2 \right. [/TEX]
Trường hợp 2: y=2, thay vào hệ ban đầu ta có:
[TEX]\left{ x = 2 \\ -x^3+ 3x + 4 = 2 \right. \Leftrightarrow x=2 \Rightarrow \left{ x=2 \\ y=2 \right. [/TEX]
Kết luận: Nghiệm của hệ phương trình đã cho là:
[TEX]\left{ x =2 \\ y = 2[/TEX]
D
duynhan1
Định hướng: Để ý đến đẳng thức [TEX]( x+ \sqrt{x^2+1}) ( \sqrt{x^2+1}-x) = 1[/TEX], như vậy từ phương trình (1) ta sẽ tìm cách chứng minh [TEX]x=-y[/TEX] bằng cách nhân lượng liên hợp.Bài 68: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}(x+\sqrt{x^2+1})(y+\sqrt{y^2+1})=1\\ y+\frac{y}{\sqrt{x^2-1}}+\frac{35}{12}=0\end{matrix}\right.[/TEX]
[/TEX]
Bài giải:
Điều kiện : [TEX]|x|>1[/TEX]
[TEX](1) \Rightarrow \left{ x + \sqrt{x^2 +1} = \sqrt{y^2 + 1 } -y \\ y + \sqrt{y^2+1} = \sqrt{x^2+1}-x \right. \Rightarrow x-y = y- x \Leftrightarrow x=-y [/TEX]
Thay vào phương trình (2) ta có:
[TEX]x+\frac{x}{\sqrt{x^2-1}}=\frac{35}{12}[/TEX]
[TEX]\Leftrightarrow \left{ x >0 \\ x^2 + \frac{x^2}{x^2 -1} + \frac{2x^2}{\sqrt{x^2-1}} = ( \frac{35}{12})^2 (3)[/TEX]
Giải (3):
Đặt [TEX]t = \sqrt{x^2-1} ( t>0)[/TEX], ta có:
[TEX]t^2 + 1 + \frac{t^2+1}{t^2} + \frac{2(t^2+1)}{t} = ( \frac{35}{12})^2[/TEX]
[TEX]\Leftrightarrow ( t + \frac{1}{t})^2 + 2 ( t + \frac{1}{t}) + 1 = \frac{1396}{144} \\ \Leftrightarrow ( t + \frac{1}{t} + 1)^2 = \frac{37^2}{12^2} \\ \Leftrightarrow t + \frac{1}{t} + 1 = \frac{37}{12} (do \ t>0) \\ \Leftrightarrow \left[ t = \frac34 \\ t = \frac43[/TEX]
Trường hợp 1: [TEX]t = \frac34 [/TEX]
[TEX]\Leftrightarrow x^2 -1 =\frac{9}{16} \\ \Leftrightarrow x = \pm \frac54 [/TEX]
Kết hợp điều kiện [TEX]\left{ |x| >1 \\ x >0 \right. [/TEX] ta suy ra [TEX]x = \frac54 \Rightarrow y = - \frac54[/TEX]
Trường hợp 2: [TEX]t = \frac43 [/TEX]
[TEX]\Leftrightarrow x^2 -1 = \frac{16}{9} \Leftrightarrow x = \pm \frac53[/TEX]
Kết hợp điều kiện [TEX]\left{ |x| >1 \\ x >0 \right. [/TEX] ta suy ra [TEX]x = \frac53 \Rightarrow y = - \frac53[/TEX]
Kết luận: Nghiệm của hệ phương trình đã cho là:
[TEX]\left[ \left{ x = \frac54 \\ y = - \frac54 \right. \\ \left{ x = \frac53 \\ y = - \frac53\right. \right. [/TEX]
D
duynhan1
Định hướng: Có 2 cách giải quyết cho bài này:Bài 67: Giải hệ phương trình:
[TEX]\left\{\begin{matrix}x+\sqrt{1-y^2}=1\\ y+\sqrt{1-x^2}=\sqrt{3}\end{matrix}\right.[/TEX]
- Lượng giác hóa
- [TEX]x = sin a, y = sin b [/TEX], bình phương và cộng 2 vế ta được [TEX]2 + 2sin a . cos b+ 2 sin b . cos a = 4 \Leftrightarrow sin(a+b) = 1[/TEX], kết hợp với đk a, b ban đầu để suy ra a, b.
- Đại số: Chuyển vế và bình phương, sau đó xác lập quan hệ giữa x và y rồi thay lại vào hệ.
Bài giải:
Điều kiện: [TEX]\left{ |x| \le 1\\ |y| \le 1[/TEX]
Với điều kiện trên ta có hệ phương trình tương đương với:
[TEX]\left{ 1-y^2 = 1 - 2x + x^2 \\ 1- x^2 = 3 - 2\sqrt{3} y + y^2 \right. \\ \Leftrightarrow \left{ x^2 + y^2 = 2x \\ x^2 + y^2 =2\sqrt{3} y - 2 \right. \\ \Leftrightarrow \left{ x = \sqrt{3} y - 1\\ ( \sqrt{3} y - 1)^2 + y^2 = 2\sqrt{3} y - 2 \right. \\ \Leftrightarrow \left{ x = \sqrt{3} y - 1 \\ ( 2y - \sqrt{3} )^2 = 0 \right. \\ \Leftrightarrow \left{ y = \frac{\sqrt{3}}{2} \\ x = \frac12 \right. (thoa\ dieu\ kien\ xac\ dinh )[/TEX]
Kết luận: Nghiệm của hệ phương trình đã cho là:
[TEX]\left{ x = \frac12 \\ y = \frac{\sqrt{3}}{2}[/TEX]
L
locxoaymgk
Bài 71: Giải PT:[TEX] x^2-4x+3=\sqrt{x+5}. [/TEX]
Bài 72:, Giải HBPT:
[TEX] \ \ \ \ \ \ \left{\begin{x^6+y^8+z^{10} \leq 1}\\{x^{2007}+y^{2009}+z^{2011} \geq 1}.[/TEX]
Bài 72:, Giải HBPT:
[TEX] \ \ \ \ \ \ \left{\begin{x^6+y^8+z^{10} \leq 1}\\{x^{2007}+y^{2009}+z^{2011} \geq 1}.[/TEX]
D
duynhan1
Định hướng: Nhận thấy có nghiệm x=4, nên bình phương đưa về phương trình bậc 4, nhưng phương trình bậc 3 nghiệm xấu quá, lại thỏa điều kiện chứ^^.Bài 71: Giải PT:[TEX] x^2-4x+3=\sqrt{x+5}. [/TEX]
Định hướng: Không.Bài 72:, Giải HBPT:
[TEX] \ \ \ \ \ \ \left{\begin{x^6+y^8+z^{10} \leq 1}\\{x^{2007}+y^{2009}+z^{2011} \geq 1}.[/TEX]
Bài giải:
Từ bpt(1) ta có: [TEX]|x|, |y|, |z| \le 1[/TEX]
Khi đó ta có:
[TEX]\left{ x^{2007} \le x^6 \\ z^{2009} \le y^8 \\ z^{2011} \le z^{10} \right. [/TEX]
[TEX]\Rightarrow1\le x^{2007}+y^{2009}+z^{2011} \le x^6+y^8+z^{10} \le 1[/TEX]
Dấu "=" xảy ra khi và chỉ khi:
[TEX](x;y;z) =(0;0;1)[/TEX] và các hoán vị.
- Status
- Không mở trả lời sau này.

