[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Câu 1:
a) Rút gọn biểu thức:
A=
(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})-xyz(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}))
b) Cho x+y+z=0; tính giá trị của biểu thức:
B=

Bài 2:
a) Tìm nghiệm nguyên của phương trình:

b) Cho
 . Chứng minh:
. Chứng minh:
^2}+\frac{y}{(z+x)^2}+\frac{z}{(x+y)^2}=0)
Bai 3:
Cho hình thang ABCD(AB//DC) có O là giao điểm của hai đường chéo. Qua O kẻ đường thẳng song song vs AB cắt AD,BC lần lượt tại M và N .
a) cm: OM = ON
b) cm:

c) S
 AOB=
AOB=
 S
S
 DOC=
DOC=
 . Tính S ABCD
. Tính S ABCD
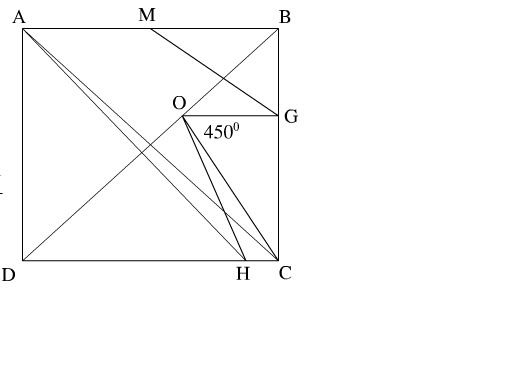
Bài 4: Cho hình vuông ABCD có O là giao điểm 2 đường chéo. Trên BC lấy điểm G trên DC lấy điểm H sao cho
 =45*. Lấy M là trung điểm của AB. cm: MG // AH
=45*. Lấy M là trung điểm của AB. cm: MG // AH
Bài 6: Cho 2 số a b thỏa mãn:
 . cm rằng:
. cm rằng:

a) Rút gọn biểu thức:
A=
b) Cho x+y+z=0; tính giá trị của biểu thức:
B=
Bài 2:
a) Tìm nghiệm nguyên của phương trình:
b) Cho
Bai 3:
Cho hình thang ABCD(AB//DC) có O là giao điểm của hai đường chéo. Qua O kẻ đường thẳng song song vs AB cắt AD,BC lần lượt tại M và N .
a) cm: OM = ON
b) cm:
c) S
Bài 4: Cho hình vuông ABCD có O là giao điểm 2 đường chéo. Trên BC lấy điểm G trên DC lấy điểm H sao cho
Bài 6: Cho 2 số a b thỏa mãn: