$\color{red}{\fbox{Toán}\bigstar\text{Hình giải tích}}$

[demon311]

Bài 1:

a) $(x-1)^2+(y-1)^2=25$

b) $B(x;y)$

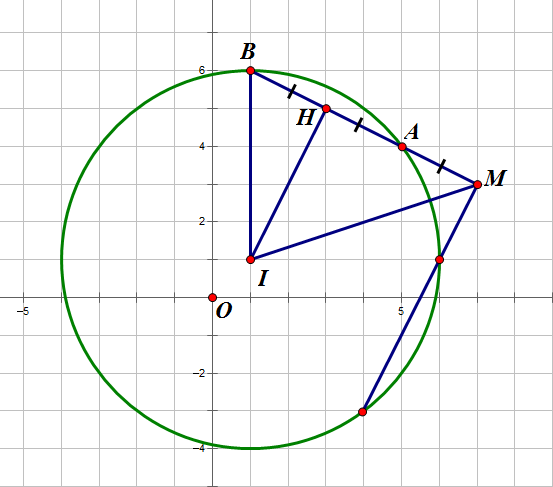
Kẻ $IH \perp AB$
Ta có:

$AH=AB \\
IM^2=IH^2+HM^2 \\
IB^2=IH^2+BH^2 \\
IM^2-IB^2=HM^2-BM^2 \\
40-25=3BH^2 \\
BH=\sqrt{ 5} \\
BM=3\sqrt{ 5} \\
(x-7)^2+(y-3)^2=45 $

Hệ:

$\begin{cases}
(x-1)^2+(y-1)^2=25 \\
(x-7)^2+(y-3)^2=45
\end{cases} \\
\begin{cases}
x=1 \\
y=6
\end{cases} \\
\\
B(1;6) \\
\overrightarrow{MB}=(-6;3) \\
pttq:\;\;\; 3(x-1)+6(y-6)=0 \\
x+2y-13=0$

 

[demon311]

Chú chỉ anh cách tìm pt tiếp tuyến của parabol đi Khoa
Gặp mấy bài ấy anh đói thôi
======================================

 

[huynhbachkhoa23]

Câu 1:

a) Câu này đơn giản.

b) Theo phương tích của đường tròn:

$MA.MB=MI^2-R^2$ mà $3MA=MB$

$\leftrightarrow MA^2=5$

$(C'): (x-7)^2+(y-3)^2=5$

$\begin{cases}
(x_A-1)^2+(y_A-1)^2=25 \\
(x_A-7)^2+(y_A-3)^2=5 \\
\end{cases}$

Giải hệ có được $A(5;4)$ hoặc $A(6;1)$

Đến đây viết phương trình qua $M$ và $A$.

 

[demon311]

Còn điểm B(4;-3) nữa quên ghi
Phương tích đó gặp lần đầu
pt tiếp tuyến nhé

 

[huynhbachkhoa23]

Chú chỉ anh cách tìm pt tiếp tuyến của parabol đi Khoa
Gặp mấy bài ấy anh đói thôi
======================================

Cho $(P): y=f(x)=ax^2+bx+c$ và điểm $A(x_0; y_0) \in (P)$. Viết phương trình tiếp tuyến tại $A$

Cách 1: Viết phương trình đường thẳng xoay quanh $A$:
$(d): m(x-x_0)+(y-y_0)=0 \leftrightarrow y=-mx+mx_0+y_0$

Tìm giao $(d)$ và $(P)$: $ax^2+bx+c=-mx+mx_0+y_0$

$\Delta = 0$

Cách 2: Đạo hàm.

$y'=f'(x)=2ax+b$

$(d): y= f'(x_0)(x-x_0)+f(x_0)$

 

[huynhbachkhoa23]

Còn điểm B(4;-3) nữa quên ghi
Phương tích đó gặp lần đầu
pt tiếp tuyến nhé

Cái phương tích thì em cũng chỉ mới học, nó như thế này

Cho đường tròn tâm $O$ bán kính $R$ và điểm $M$ tuỳ ý sao cho không nằm trên đường tròn. Hai đường thẳng qua $M$, đường thứ nhất cắt đường tròn tại $A$ và $B$, đường thứ 2 cắt đường tròn tại $C$ và $D$, ta có $MA.MB=MC.MD=|MO^2-R^2|$

Hệ quả: Nếu $MC$ là tiếp tuyến thì $MA.MB=MC^2$

Mấy dạng toán như trên hay gặp ở lớp 10 sử dụng phương tích cũng tiện lắm

 

[demon311]

Anh thì mới biết cái tiếp tuyến thôi, nhưng mà vẫn hiểu, chẳng qua là Pitago nên nó ra cái của chú

 

[huynhbachkhoa23]

Em xin đóng góp 2 bài khá dễ về lý thuyết, mấy hôm nữa tới chương Đường tròn Elip thì cho qua lý thuyết này.

1. Chứng minh $(E): \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ với $a,b>0$ có hệ tham số là:

$(E): \begin{cases}x=a\sin t \\ y=b\cos t \\ \end{cases}$

hoặc

$(E): \begin{cases}x=a\cos t \\ y=b\sin t \\ \end{cases}$

2. Cho Elip có độ dài trục ngang là $a$, trục dọc là $b$, tâm là $I(x_0; y_0)$.

a) Viết phương trình Elip $(E)$ đó.

b) Dựa vào kết quả bài 1 hãy viết phương trình tham số cho $(E)$ ở câu a) (lấy phương trình tham số đầu tiên).

c) Viết phương trình tham số của đường tròn bán kính $R$, tâm $I(x_0;y_0)$

Hoàn toàn là dựa vào kiến thức lớp 10.

Nếu câu 1 không nghĩa ra thì bôi đen dòng phía sau đây =)): $\cos^2 \alpha + \sin^2 \alpha =1$

Giải luôn.

Bài 1:

1)Ta chứng minh ngược lại
x=asint <=> $x^{2}=a^{2}.sin^{2}t$
y=bcost <=> $y^{2}=b^{2}.cos^{2}t$
Thế vào Pt chính tắc của (E) sẽ được $sin^{2}t+cos^{2}t=1$ luôn đúng

Bài 2:

a) Áp dụng quy tắc tịnh tiến hoặc quy tắc dời hệ trục: $(E):\dfrac{(x-x_0)^2}{a^2}+\dfrac{(y-y_0)^2}{b^2}=1$

b) $\begin{cases}
x-x_0=a.\sin t \\
y-y_0=b.\cos t\\
\end{cases} \rightarrow \begin{cases}
x=a.\sin t + x_0 \\
y=b.\cos t + y_0 \\
\end{cases}$

c) Đường tròn coi như là một Elip có độ dài 2 trục bằng nhau.

$\begin{cases}
x=R.\sin t + x_0 \\
y=R.\cos t + y_0 \\
\end{cases}$

Lưu ý: Elip không nhất thiết có trục lớn là trục ngang, trục bé là trục dọc như trong SGK.

Trục nào dài hơn thì trục đó chứa tiêu điểm.

 

[super_saiyan]

kinh nhỉ mấy bác học được tới cái gì đây nhìn trông choáng quá .

 

[huynhbachkhoa23]

Bài 2: Cho đồ thị $(T): y=x^3-6x^2+7x+5$

a) Tìm tâm đối xứng của đồ thị.
b) Đồ thị có bao nhiêu giao điểm với trục tung, bao nhiêu giao điểm với trục hoành.

Bài 3: Cho $(P): y= \dfrac{1}{4}(x-1)^2+2$

a) Tìm GTLN, GTNN của $y$ trong khoảng $[-1;5]$
b) Viết phương trình tiếp tuyến cho $(P)$ tại $x=2$
c) Tìm toạ độ tiêu điểm và viết phương trình đường chuẩn. (không cần dời hệ)

Bài 2:

a) $(T): y= (x-2)^3-5(x-2)+3$

Tâm đối xứng $M(2;3)$

b) Tập xác định $\mathbb{T}=\mathbb{R}$

$\rightarrow$ có 1 giao điểm với trục tung.

$y(-1)=-9; y(1)=7; y(3)=-1; y(4)=1$

$-1 < 1 < 3 < 4$

Vậy đồ thị có 3 giao điểm với trục hoành.

Bài 3:

a) Toạ độ đỉnh Parabol: $x_0=1 \in [-1;5]$

$\rightarrow \text{min}y=2 \leftrightarrow x=1$

$|1-(-1)|<|1-5| \rightarrow \text{max}y=6 \leftrightarrow x=5 \;\;\;\; (x \in [-1;5])$

b) $x=2 \rightarrow y=\dfrac{9}{4}$

$y'=\dfrac{1}{2}x-\dfrac{1}{2}$

$\rightarrow (d):\dfrac{1}{2}(x-2)+\dfrac{9}{4}$

c) Với Parabol $y=ax^2+bx+c$ có $a>0$, toạ độ tiêu điểm $F(x_0;y_0+\dfrac{1}{4a})$ với $(x_0;y_0)$ là toạ độ đỉnh Parabol.

$F(1;3)$

$(\Delta): y=1$

 

[bigtbang]

bài này dễ nè
cho pt X^2+Y^2-2mX-4(m-2)Y-m+6=0 (1)
1 tìm m để (1)là pt đường tròn (c)
2 tìm tập hợp tâm I(m) của họ đường tròn (c)

 

[huynhbachkhoa23]

bài này dễ nè
cho pt X^2+Y^2-2mX-4(m-2)Y-m+6=0 (1)
1 tìm m để (1)là pt đường tròn (c)
2 tìm tập hợp tâm I(m) của họ đường tròn (c)

1. Em không quen dùng công thức khai triển nên đưa về dạng toạ độ tâm:

$(C): x^2-2mx+m^2+y^2-4(m-2)y+4(m-2)^2=m^2+4(m-2)^2+m-6$

$\leftrightarrow (C): (x-m)^2+[y-2(m-2)]^2=5(m-1)(m-2)$

$D_{m}=R / \text{{1;2}}$

2. Biểu diễn tâm dưới dạng phương trình tham số $m$:
$\begin{cases}
x=m\\
y=2m-4\\
\end{cases}$

$\vec{n}=(2;-1)$

$(d): 2x-y-4=0$