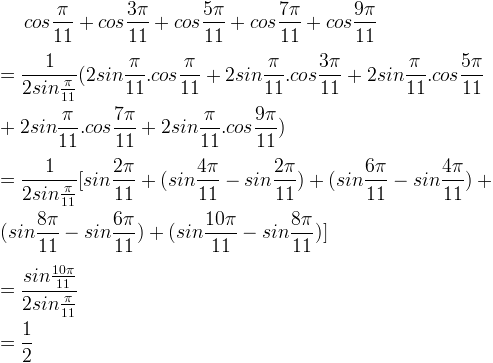D
duynhan1
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
CHUYÊN ĐỀ LƯỢNG GIÁC
Để bắt đầu cuộc hành trình, ta không thể không chuẩn bị hành trang lên đường. Toán học cũng vậy. Muốn khám phá cái hay cái đẹp của lượng giác, ta cần có những "vật dụng" chắc chắn và hữu dụng. Vì vậy mình lập ra topic này để các bạn cùng nhau post những bài lượng giác hay để chúng ta cùng nhau thảo luận và làm quen với dạng toán này, chuẩn bị kiến thức cho phần phương trình lượng giác lớp 11.
Mong các bạn ủng hộ.
Mình xin post trước 2 bài:
Bài 1:Tính
a) [TEX]tan 9^o -tan 27^o - tan 63^o + tan 81^o[/TEX]
b) [TEX]\frac{1}{sin 18^o} - \frac{1}{sin 54^o}[/TEX]
Bài 2: Rút gọn:
a) [TEX]cos ({\pi}/{11}) + cos ({3\pi}/{11}) + cos ({5\pi}/{11})+ cos ({7\pi}/{11}) +cos ({9\pi}/{11})[/TEX]
b) [TEX]sin ({2 \pi}/{7}) + sin ({4 \pi}/{7}) + sin ({6 \pi}/{7})[/TEX]
c) [TEX]sin ({\pi}/{11}) + sin ({2 \pi}/{11}) + .....+sin ({10 \pi}/{11})[/TEX]
Last edited by a moderator: