 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Giúp mik câu này ạ
View attachment 216487
Ta có:
Cường độ điện trường do [imath]A[/imath] tác dụng lên [imath]M[/imath]: [imath]E_1 =\dfrac{kq}{x^2+a^2}[/imath]
Tương tự cường độ điện trường do [imath]B[/imath] tác dụng cũng thế.
Góc hợp bởi cường độ điện trường [imath]E_1[/imath] này với đường trung trực qua [imath]M[/imath] là: [imath]\cos \alpha = \dfrac{x}{\sqrt{x^2+a^2}}[/imath]
Cường độ tác dụng lên [imath]M[/imath]: [imath]E = 2.E_1.\cos \alpha[/imath]
Thay tất cả vào biện luận tìm được [imath]E[/imath] đạt cực đại khi [imath]x= \dfrac{a\sqrt{2}}{2}[/imath]
Khi này [imath]E_{max} = \dfrac{4kq}{3\sqrt{3}a^2}[/imath]
Chúc em học tốt
Tham khảo thêm tại Chuyên đề điện tích điện trường
chị chỉ rõ cho em chỗ tính x đc ko ạ
Mình phân tích ra nè!
[imath]a^2 + h^2 = \dfrac{a^2}{2} + \dfrac{a^2}{2} + h^2[/imath]
Nên: [imath](a^2+h^2)^3 \geq \dfrac{27}{4}a^4.h^2[/imath] (BĐT Cô si dành cho mũ 3)
Vậy: [imath](a^2 + h^2)^{\dfrac{3}{2}} \geq 3.\sqrt{3}{2}.a^2.h[/imath]
Dấu "=" xảy ra khi: [imath]\dfrac{a^2}{2} = h^2[/imath]
Ổn chưa em nhỉ?
Tham khảo thêm tại: Những kiến thức Toán dành cho dân Lý
a và h là gì vậy chị, nó ko khớp vs ẩn đề bài đko ạ ?
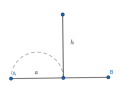
a và h là gì vậy chị, nó ko khớp vs ẩn đề bài đko ạ ?

