@all: các em cần chú ý phân biệt từ
vận tốc và
tốc độ, anh thấy nhiều bạn hay dùng lẫn hai cái này
Vận tốc (velocity) là một đại lượng vector có cả hướng + độ lớn. Trong các biểu thức đại số thì hướng của nó có thể được xác định = dấu của giá trị.
Tốc độ (speed) là 1 đại lượng vô hướng. Nó là độ lớn của vận tốc (tức giá trị tuyệt đối).
Anh cũng ko biết ý đồ người ra đề ở đây dùng từ vận tốc với nghĩa nào nên đành post hai hướng.
Thực tế ở nước ta rất nhiều giáo viên dùng lẫn lộn các khái niệm, không đúng chuẩn, ko đúng bản chất. Mà cũng ko riêng gì môn lý, các môn khác cũng thế. Điển hình nhất là môn toán. Bất đẳng thức [TEX]\frac{a+b}{2} \geq \sqrt{ab}[/TEX] mà chúng ta thuờng gọi là BDT Cauchy này tên chính thức của nó là bất đẳng thức AM-GM (Arithmetic Mean - Geometric Mean) <bất đẳng thức liên hệ giữa trung bình số học và hình học>. Quốc tế chẳng ai gọi là BDT Cauchy cả, Cauchy ko phải là người phát minh ra BDT này mà ông chỉ là người đưa ra một phương pháp chứng minh rất hay cho nó - phương pháp Cauchy ngược. Không biết tình trạng như thế này còn kéo dài đến bao h nữa :-??
Trường hợp 1: ý người ra đề là chỉ xét độ lớn chứ ko xét dấu (tức tốc độ)
[TEX]v=\omega\sqrt{A^2-x^2}[/TEX] (1)
khi [TEX]v=\frac{1}{2}v_{max}=\frac{1}{2}\omega A[/TEX] lắp vào (1) thì được
[TEX]x=\pm \frac{\sqrt{3}}{2}A[/TEX]
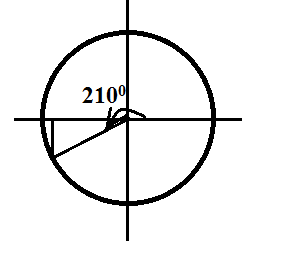
Dùng đường tròn lượng giác suy ra được góc quét là [TEX]\frac{\pi}{6}\Rightarrow 5\pi t=\frac{\pi}{6}\Rightarrow t=\frac{1}{30} (s)[/TEX]
Trường hợp 2: ý người ra đề là đúng theo chuẩn, tức xét vận tốc đúng định nghĩa.
Làm tương tự nhưng bây giờ để [TEX]v>0[/TEX] thì [TEX]x={-}\frac{\sqrt{3}}{2}A[/TEX]
vậy góc quét được là [TEX]\frac{7\pi}{6}[/TEX]
Nên [TEX]t=\frac{7}{30} (s)[/TEX]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
