Toán 10 [11A]™ - Chuyên đề PTĐT

[kieuoanh_1510]

8.
[tex]\left\{ \begin{array}{l} 3y=\frac{{y}^{2}+2}{{x}^{2}} \\ 3x=\frac{{x}^{2}+2}{{y}^{2}} \end{array} \right.[/tex]

????????có sai k nhỉ?????????
ghét toán!

 

[nach_rat_hoi]

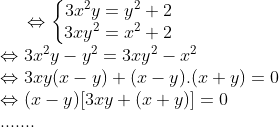
????????có sai k nhỉ?????????
ghét toán!

Đúng rồi, k có gì sai cả..........................................:-SS:-SS:-SS:-SS
Chưa điều kiện thôi. =))

 

[kieuoanh_1510]

Đúng rồi, k có gì sai cả..........................................:-SS:-SS:-SS:-SS
Chưa điều kiện thôi. =))

điều kiện hả?????????

điều kiện gì!....hơn năm rồi chưa động tới cái này!!!!!!!!!

(cái kiểu cười châm biếm! (_ _)!)

 

[tieuvan95]

điều kiện dưới mẫu đó oanh. x#o, y#0.......................................

 

[kieuoanh_1510]

ặc!!!!!!
tớ nhìn vào bài làm của tớ! ......không có mẫu
=)) =)) =))

hix.....cái tội này là không thể dung thứ!!!!!!!!!!!!!hixxxxxxxxxx

 

[nach_rat_hoi]

ặc!!!!!!
tớ nhìn vào bài làm của tớ! ......không có mẫu
=)) =)) =))

hix.....cái tội này là không thể dung thứ!!!!!!!!!!!!!hixxxxxxxxxx

HÁ HÁ, vậy lấy cái hệ cùi bắp ấy ở đâu ra vậy. =)) =)) =))=)) =)) =))=)) =)) =))=)) =)) =))=)) =)) =))=)) =)) =))=)) =)) =))=)) =)) =))

 

[hoathuytinh16021995]

ặc!!!!!!
tớ nhìn vào bài làm của tớ! ......không có mẫu
=)) =)) =))

hix.....cái tội này là không thể dung thứ!!!!!!!!!!!!!hixxxxxxxxxx

cái này không phải chuyển vế hả?
[TEX] \left\{\begin{matrix}3{x}^{2}y -{y}^{2}=2 & \\ 3x{y}^{2}-{x}^{2}=2 &\end{matrix}\right.\Rightarrow 3{x}^{2}y-{y}^{2}=3x{y}^{2}-{x}^{2}[/TEX]
............
không phải như vậy sao?
cần gì mẫu nhỉ?
huhu lại ngu nữa oyyyyyyy!

 

[hoi_a5_1995]

9.
[tex]\left\{ \begin{array}{l} (x-y)({x}^{2}-{y}^{2})=3 \\ (x+y)({x}^{2}+{y}^{2})=15 \end{array} \right.[/tex]


[tex]\left\{ \begin{array}{l} (x-y)^2(x +y)=3 \\ (x+y)((x - y)^{2}+2xy=15 \end{array} \right.[/tex]


[TEX] \frac{(x - y)^2}{(x - y)^2 +2xy} = \frac{3}{5} [/TEX]


[TEX] dat\ u = (x - y)^2 ; p = xy [/TEX]


dễ dàng => [TEX] 2u^2 = p [/TEX]


[TEX] 2 (x - y)^2 = xy [/TEX]

tiếp tục nha

tìm ngay ra x = \frac{y}{4} ; x =.........[/TEX]

 

[hoathuytinh16021995]

10.

[TEX](1)\Leftrightarrow \left\{\begin{matrix}(x-y)(2x+y)= 9& \\ (x-y)^3=9(2x+y) & \end{matrix}\right[/TEX].
đặt [TEX]\left\{\begin{matrix}x-y= a & \\ 2x+y =b & \end{matrix}\right.[/TEX]
đến đây là xong nhé!

 

[nach_rat_hoi]

[tex]\left\{ \begin{array}{l} x = 8\sqrt{2} cost \\ y = 8\sqrt{2}sint\end{array} \right.[/tex]
t thuộc R

Pt(1) [TEX] <=> \sqrt{8\sqrt{2}( cost + sint)} + \sqrt{8\sqrt{2}(cost - sint ) = 4 [/TEX][TEX] [/TEX]

[TEX]<=> 16\ cost + 4\sqrt{\sqrt{2} . 2 . cos2t} = 16 [/TEX]

[TEX]<=> \sqrt{\sqrt{2} . 2 . cos2t} = 4(1 - \sqrt{2}cost )[/TEX]

Mọi người giải ra nhé

Bài này làm thế này sẽ mất nghiệm em nhé!

khi e đặt như thế thì chỉ xét -8căn2<x<8căn2 và -8căn2<y<8căn2

Mà trong khi đó x,y chạy trên đâu????

 

[acidnitric_hno3]

7.
[tex]\left\{ \begin{array}{l} \sqrt{{x}^{2}+{y}^{2}}+\sqrt{2xy}=8\sqrt{2} \\ \sqrt{x}+\sqrt{y}=4 \end{array} \right.[/tex]

Đk: x, y \geq0
[tex]\left\{ \begin{array}{l} \sqrt{2.({x}^{2}+{y}^{2})}+2\sqrt{xy}=16 \\ x+y + 2\sqrt{xy} =16 \end{array} \right.[/tex]
=> [tex]\sqrt{2.({x}^{2}+{y}^{2})} = x+y[/tex]
Bình phương 2 vế => [tex]2(x^2+y^2) = x^2 + 2xy + y^2 => (x-y)^2 = 0=> x = y[/tex]
Thế vào pt 2 =>[tex] x = y = 4[/tex]

 

[nach_rat_hoi]

Đk: x, y \geq0
<=>[tex]\left\{ \begin{array}{l} {x}^{2}+{y}^{2}+ 2xy +2\sqrt{2xy(x^2+y^2)}=128 \\ \x+y + 2\sqrt{xy}= 16\end{array} \right.[/tex]
<=>[tex]\left\{ \begin{array}{l} (x+y)^2 +2x\sqrt{2xy}+ 2y\sqrt{2xy}}=128 \\ \x+y + 2\sqrt{xy}= 16\end{array} \right.[/tex]

<=>[tex]\left\{ \begin{array}{l} (x+y)^2 +2(x+y)\sqrt{2xy}}=128 \\ \ x+y + 2\sqrt{xy}= 16\end{array} \right.[/tex]
Đặt [tex]x+y = u;\sqrt{xy} = v[/tex]
<=>[tex]\left\{ \begin{array}{l} u^2 +2\sqrt{2}uv=128 \\ \ u + 2v= 16\end{array} \right.[/tex]
Giải u, v

Cái dâu <=> thứ 2 nàng xem lại hộ anh với, ac ac, sao mà dung định lý acid để đưa nó ra khỏi căn ak??

 

[acidnitric_hno3]

Ừ nhỉ=)) Nhầm tai hại =)) Chờ edit lại=))
_________________________________________________________________
Xí cả hủ

 

[doraemonkute]

1.
7.
[tex]\left\{ \begin{array}{l} \sqrt{{x}^{2}+{y}^{2}}+\sqrt{2xy}=8\sqrt{2} \\ \sqrt{x}+\sqrt{y}=4 \end{array} \right.[/tex [COLOR="Blue"]Mọi người làm rồi post lời giải lên sớm nào![/COLOR][/QUOTE] [FONT="Times New Roman"][SIZE="4"]ĐKXĐ:[TEX]x;y\geq0[/TEX]
hệ pt\Leftrightarrow [TEX]\left\{\begin{matrix} &\sqrt{2(x^2+y^2)}+2\sqrt{xy}=16 \\ & x+y+2\sqrt{xy}=16 \end{matrix}\right.[/TEX]
=> [TEX]\sqrt{2x^2+2y^2}=x+y[/TEX]
\Leftrightarrow [TEX]2x^2+2y^2=x^2+y^2+2xy[/TEX] ([TEX]x+y\geq 0[/TEX])
\Leftrightarrow [TEX](x-y)^2=0[/TEX]
\Leftrightarrow x=y
thế vào pt thứ 2 đc [TEX]2\sqrt{x}=4[/TEX] \Leftrightarrow x=y=4[/SIZE][/FONT]

 

[doraemonkute]

1.
6.
[tex]\left\{ \begin{array}{l} y+x.{y}^{2}=6{x}^{2} \\ 1+{x}^{2}.{y}^{2}=5.{x}^{2} \end{array} \right.[/tex]
Mọi người làm rồi post lời giải lên sớm nào!

+Với x=0 thì hệ trở thành :[TEX]\left\{\begin{matrix} &y=0 \\ & 1=0\end{matrix}\right.[/TEX]
(vô lí)
+[TEX]x\neq 0[/TEX] HPT \Leftrightarrow [TEX]\left\{\begin{matrix}\frac{y}{x^2}+\frac{y^2}{x}=6 & \\ \frac{1}{x^2}+y^2=5& \end{matrix}\right.[/TEX]
Đặt [TEX]u=\frac{1}{x}[/TEX] ta có
[TEX]\left\{\begin{matrix}u^2y+uy^2=6 & \\ u^2+y^2=5& \end{matrix}\right.[/TEX]
\Leftrightarrow [TEX]\left\{\begin{matrix}u+y=3 & \\ uy=2& \end{matrix}\right.[/TEX]
=>u,y=>x
hệ có 2 nghiệm (x;y) là (1;2) và (1/2;1)

 

[nach_rat_hoi]

+Với x=0 thì hệ trở thành :[TEX]\left\{\begin{matrix} &y=0 \\ & 1=0\end{matrix}\right.[/TEX]
(vô lí)
+[TEX]x\neq 0[/TEX] HPT \Leftrightarrow [TEX]\left\{\begin{matrix}\frac{y}{x^2}+\frac{y^2}{x}=6 & \\ \frac{1}{x^2}+y^2=5& \end{matrix}\right.[/TEX]
Đặt [TEX]u=\frac{1}{x}[/TEX] ta có
[TEX]\left\{\begin{matrix}u^2y+uy^2=6 & \\ u^2+y^2=5& \end{matrix}\right.[/TEX]
\Leftrightarrow [TEX]\left\{\begin{matrix}u+y=3 & \\ uy=2& \end{matrix}\right.[/TEX]
=>u,y=>x
hệ có 2 nghiệm (x;y) là (1;2) và (1/2;1)

Good!!!

Có thể đặt cách khác: [TEX]\frac{1}{x}+y=u[/TEX] và [TEX]v=\frac{y}{x}[/TEX]

 

[doraemonkute]

2.
[tex]\left\{ \begin{array}{l} \sqrt{x+y}+\sqrt{x-y}=4 \\ {x}^{2}+{y}^{2}=128 \end{array} \right.[/tex]

Mọi người làm rồi post lời giải lên sớm nào!

HPT \Leftrightarrow [TEX]\left\{\begin{matrix}\sqrt{x+y}+\sqrt{x-y} =4& \\ (x+y)^2+(x-y)^2=256&\end{matrix}\right. [/TEX]
Đặt [TEX]\left\{\begin{matrix}\sqrt{x+y}=u\geqslant 0& \\ \sqrt{x-y}=v\geq 0 &\end{matrix}\right.[/TEX]
hệ pt trở thành: [TEX]\left\{\begin{matrix}u+v=4 & \\ u^4+v^4=256& \end{matrix}\right.[/TEX]
\Leftrightarrow [TEX]\left\{\begin{matrix}(u+v)^4=256 & \\ u^4+v^4=256& \end{matrix}\right.[/TEX]
\Rightarrow [TEX](u+v)^4-u^4-v^4=0[/TEX]
\Leftrightarrow [TEX]uv(2u^2+3uv+2v^2)=0[/TEX]
\Leftrightarrow uv=0 hoặc [TEX]2u^2+3uv+2v^3=0[/TEX]

Giải 2 pt ra u,v =>x,y
Hệ có 2 nghiệm (x;y) là (8;8) và (8;-8)

 

[acidnitric_hno3]

2.
[tex]\left\{ \begin{array}{l} \sqrt{x+y}+\sqrt{x-y}=4 \\ {x}^{2}+{y}^{2}=128 \end{array} \right.[/tex]


5.
[tex]\left\{ \begin{array}{l} x(x+2)(2x+y)=9 \\ {x}^{2}+4x+y=6 \end{array} \right.[/tex]

2. [tex]\left\{ \begin{array}{l} \sqrt{x+y}+\sqrt{x-y}=4 \\ {x}^{2}+{y}^{2}=128 \end{array} \right.[/tex]

[tex]\left\{ \begin{array}{l} 2x + 2\sqrt{x^2-y^2}=16 \\ {x}^{2}+{y}^{2}=128 \end{array} \right.[/tex]

[tex]\left\{ \begin{array}{l} x^2-y^2 = (8-x)^2 \\ {x}^{2}+{y}^{2}=128 \end{array} \right.[/tex] Nhớ điều kiện để bình phương (x<=8)
[tex]\left\{ \begin{array}{l} x^2-y^2=64-16x + x^2 \\ {x}^{2}=128- {y}^{2} \end{array} \right.[/tex]
[TEX]=> 64-16x+x^2 = 2x^2-128=> X^2 + 16x-192=0=> x = 8; x = -24[/TEX]( loại vì [TEX]x^2+y^2 = 128 => x^2<128 => -\sqrt{128}<=x<=\sqrt{128}[/TEX]
5.
[tex]\left\{ \begin{array}{l} x(x+2)(2x+y)=9 \\ {x}^{2}+4x+y=6 \end{array} \right.[/tex]
5.
[tex]\left\{ \begin{array}{l} (x^2+2x)(2x+y)=9 \\ {x}^{2}+2x+2x+y=6 \end{array} \right.[/tex]
Đặt [TEX]u = x^2 + 2x; v = 2x+y[/TEX]
=>
[tex]\left\{ \begin{array}{l} uv=9 \\ u+v=6 \end{array} \right.[/tex]

 

[acidnitric_hno3]

3.
[tex]\left\{ \begin{array}{l} (x+y)(1+\frac{1}{xy})=5 \\ ({x}^{2}+{y}^{2})(1+\frac{1}{{(x.y)}^{2}})=49 \end{array} \right.[/tex]

[tex]\left\{ \begin{array}{l} (x+y)(1+\frac{1}{xy})=5 \\ ({x}^{2}+{y}^{2})(1+\frac{1}{{(x.y)}^{2}})=49 \end{array} \right.[/tex]

[tex]\left\{ \begin{array}{l} x+ y + \frac{1}{y} + \frac{1}{x}=5 \\ {x}^{2}+{y}^{2} + \frac{1}{y^2} + \frac{1}{x^2}=49 \end{array} \right.[/tex]
[tex]\left\{ \begin{array}{l} x + \frac{1}{x}+ y+ \frac{1}{y} =5 \\ {x}^{2}+\frac{1}{x^2}+ {y}^{2} + \frac{1}{y^2} =49 \end{array} \right.[/tex]
Đặt [TEX]x+\frac{1}{x} =u, y+\frac{1}{y} = v =>{x}^{2}+\frac{1}{x^2}= u^2-2; {y}^{2} + \frac{1}{y^2} = v^2-2 [/TEX]
=>[tex]\left\{ \begin{array}{l} u+v =5 \\ u^2-2+v^2-2 =49 \end{array} \right.[/tex]
=> u;v

 

[nach_rat_hoi]

Bài tập mới nè!

1.
[tex]\left\{ \begin{array}{l} 5{x}^{2}y-4x{y}^{2}+3{y}^{3}-2(x+y)=0 \\ xy({x}^{2}+{y}^{2})+2={(x+y)}^{2} \end{array} \right.[/tex]

2.
[tex]\left\{ \begin{array}{l} x-2y-\sqrt{xy}=0 \\ \sqrt{x-1}-\sqrt{2y-1}=1 \end{array} \right.[/tex]

3.
[tex]\left\{ \begin{array}{l} xy+x+y={x}^{2}-2{y}^{2} \\ x\sqrt{2y}-y\sqrt{x-1}=2x-2y \end{array} \right.[/tex]

4.
[tex]\left\{ \begin{array}{l} x+\sqrt{1-{y}^{2}}=1 \\ y+\sqrt{1-{x}^{2}}=1 \end{array} \right.[/tex]

5.
[tex]\left\{ \begin{array}{l} {x}^{3}+3y={y}^{3}+3x \\ 3{x}^{2}+{y}^{2}=1 \end{array} \right.[/tex]