V
vansang02121998
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. Quy tắc
1. Mỗi lần chỉ được đăng 2 bài, không hơn không kém
2. Chỉ khi nào giải đúng cả 2 bài mới được post bài khác ( ai post cũng được )
3. Không spam. Bài sai và bài spam xóa hết.
4. Lưu ý đây không là event nên không có phần thưởng
II. Kiến thức và kĩ năng cơ bản
1. Các phương pháp cơ bản chứng minh bất đẳng thức
a, Phương pháp biến đổi tương đương
- Đưa về bình phương và tổng bình phương
- Đưa về dạng tích để xét dấu
- Đưa về tổng các số cùng dấu
b, Phương pháp sử dụng bất đẳng thức
c, Phương pháp phản chứng
d, Phương pháp làm trội, Làm giảm
2. Một số BĐT cơ bản cần nhớ
a)
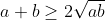
Tổng quát
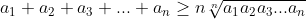
Dấu "=" xảy ra khi
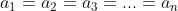
b)
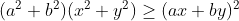
Tổng quát
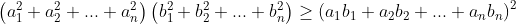
Dấu "=" xảy ra khi
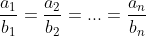

Tổng quát
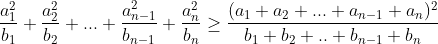
Dấu "=" xảy ra khi
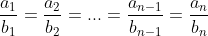

Hệ quả
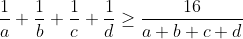
Dấu "=" xảy ra khi
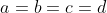
&space;\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}&space;\geq&space;\frac{3}{2})
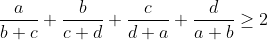
Dấu "=" xảy ra khi
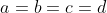
Ngoài ra còn một số nữa các bạn tự tìm hiểu
III. Một số bài tập
Bài 1: Cho 3 số dương a; b; c. Chứng minh

Bài 2: Chứng minh bất đẳng thức Cauchy cho 3 bộ ( áp dụng bất đẳng thức Cauchy cho 2 bộ )
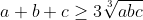
Mở hàng ngon cho các bạn đó nghe!!!
1. Mỗi lần chỉ được đăng 2 bài, không hơn không kém
2. Chỉ khi nào giải đúng cả 2 bài mới được post bài khác ( ai post cũng được )
3. Không spam. Bài sai và bài spam xóa hết.
4. Lưu ý đây không là event nên không có phần thưởng
II. Kiến thức và kĩ năng cơ bản
1. Các phương pháp cơ bản chứng minh bất đẳng thức
a, Phương pháp biến đổi tương đương
- Đưa về bình phương và tổng bình phương
- Đưa về dạng tích để xét dấu
- Đưa về tổng các số cùng dấu
b, Phương pháp sử dụng bất đẳng thức
c, Phương pháp phản chứng
d, Phương pháp làm trội, Làm giảm
2. Một số BĐT cơ bản cần nhớ
a)
Tổng quát
Dấu "=" xảy ra khi
b)
Tổng quát
Dấu "=" xảy ra khi
Tổng quát
Dấu "=" xảy ra khi
Hệ quả
Dấu "=" xảy ra khi
Dấu "=" xảy ra khi
Ngoài ra còn một số nữa các bạn tự tìm hiểu
III. Một số bài tập
Bài 1: Cho 3 số dương a; b; c. Chứng minh
Bài 2: Chứng minh bất đẳng thức Cauchy cho 3 bộ ( áp dụng bất đẳng thức Cauchy cho 2 bộ )
Mở hàng ngon cho các bạn đó nghe!!!
Last edited by a moderator:

