leduymanh2005
[imath]a/[/imath]
Giả sử sóng truyền theo chiều dương trục [imath]Ox[/imath], ban đầu kích thích [imath]O[/imath] dao động đi lên.
Khi đó tại thời điểm [imath]t_1[/imath] điểm [imath]M[/imath] đang đi xuống, tại thời điểm [imath]t_2[/imath] nó đi lên và cả hai thời điểm thì li độ của điểm [imath]M[/imath] đều là [imath]2cm[/imath]
Từ hình vẽ dễ thấy biên độ [imath]A=4cm[/imath]
Trên đường tròn, điểm pha tại thời điểm [imath]t_1[/imath] là [imath]P_1[/imath], tại [imath]t_2[/imath] là [imath]P_2[/imath]
Quãng đường mà điểm [imath]M[/imath] đi được từ [imath]t_1[/imath] đến [imath]t_2[/imath]:
[imath]S=2+4+4+2=12cm[/imath]
Theo bài ra: [imath]S=\dfrac{2}{3}\lambda \Rightarrow \lambda = 18cm[/imath]
Thời gian đi quãng đường [imath]S[/imath] là:
[imath]t=\dfrac{S}{v_{tb}}=\dfrac{12}{12}=1s[/imath]
Trên đường tròn, dễ dàng suy ra góc quét [imath]\Delta \varphi = \dfrac{4\pi}{3}rad[/imath]
Tần số góc: [imath]\omega = \dfrac{\Delta \varphi}{t}=\dfrac{4\pi}{3} \ rad/s[/imath]
Tốc độ truyền sóng: [imath]v=\dfrac{\lambda}{T}=\dfrac{\lambda.\omega}{2\pi}=12cm/s[/imath] | 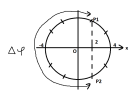 |
[imath]b/[/imath]
Từ [imath]t=0[/imath] đến [imath]t_1=0,25s[/imath], điểm pha quét được cung là: [imath]\Delta \varphi _1 = 0,25.\omega = \dfrac{\pi}{3}rad[/imath]
Từ điểm pha [imath]P_1[/imath] ta quay ngược chiều dương một cung [imath]\dfrac{\pi}{3}rad[/imath] tìm được điểm pha ban đầu [imath]P_0[/imath] như hình vẽ. suy ra pha ban đầu bằng [imath]0[/imath]
Phương trình truyền sóng tại [imath]O[/imath]:
[imath]u_O = A\cos \omega t = 4\cos \dfrac{4\pi}{3}t (cm)[/imath] |  |
[imath]c/[/imath]
- Phương trình sóng tại [imath]P[/imath]: [imath]u_P=A \cos (\omega t - \dfrac{2\pi.4,25}{\lambda})=4\cos (\dfrac{4\pi}{3}t-\dfrac{17\pi}{36}) = 4\angle -\dfrac{17\pi}{36}[/imath]
- Phương trình sóng tại [imath]M[/imath]: [imath]u_M=A \cos (\omega t - \dfrac{2\pi.1,25}{\lambda})=4\cos (\dfrac{4\pi}{3}t-\dfrac{5\pi}{36}) = 4\angle -\dfrac{5\pi}{36}[/imath]
- Phương trình sóng tại [imath]N[/imath]: [imath]u_N=A \cos (\omega t - \dfrac{2\pi.2,25}{\lambda})=4\cos (\dfrac{4\pi}{3}t-\dfrac{\pi}{4})= 4\angle -\dfrac{\pi}{4}[/imath]
Giả sử khi [imath]3[/imath] điểm thẳng hàng, sợi dây có hình dạng như hình bên.
Khi đó: [imath]\alpha = \beta \Rightarrow \tan \alpha = \tan \beta[/imath]
[imath]\hArr \dfrac{u_M-u_N}{2,25-1,25}=\dfrac{u_P+u_N}{4,25-2,25}[/imath]
[imath]\hArr 2u_M -3u_N-u_P=0[/imath]
Thay [imath]u_M,u_N,u_P[/imath] ở trên vào suy ra [imath]2,3\angle1,74 = 0[/imath]
[imath]\hArr 2,3\cos (\dfrac{4\pi}{3}-1,74)=0 \Rightarrow \dfrac{4\pi}{3}t-1,74=\dfrac{\pi}{2}+k 2\pi , k\in Z[/imath]
Để [imath]t>t_2[/imath] và [imath]t[/imath] nhỏ nhất thì [imath]t\approx 2,29s[/imath] khi [imath]k=1[/imath]
Vậy tính từ thời điểm [imath]t_2=t_1+1=1,25s[/imath], khoảng thời gian ngắn nhất để [imath]3[/imath] điểm thẳng hàng là: [imath]\Delta t = 2,29-1,25=1,04s[/imath] |  |
Chúc bạn học tốt!
-------
Xem thêm:
Tổng hợp những điều quan trọng trong chương Sóng cơ
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

