[tex](p): 2x-y-2z-2=0[/tex]
[tex](d): \frac{x}{-1}=\frac{y+1}{2}=\frac{z-2}{1}[/tex]
ý tưởng:
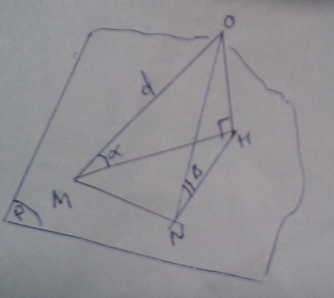
(q) là mp di động chứa (d) nên xoay quanh (d). Chứng minh (q) hợp với (p) 1 góc min, khi nó hợp với (p) 1 góc đúng bằng góc giữa (d) hợp với (p), như trong hình thì là [tex]\alpha[/tex]
chứng minh
giả sử (q) quay đến 1 vị trí bất kỳ nào khác và ký hiệu góc (q) hợp bởi (p) là [tex]\beta[/tex] như hình. (q) khi đó chính làmp (omn)
hiển nhiên
[tex]on \perp mn[/tex]
[tex]oh\perp mn[/tex]
(vì mn là giao tuyến của (p) và (q))
do đó tam giác mnh vuông tại n. Hm là cạnh huyền => hm > hn
tam giác ohm vuông ở h [tex]\rightarrow \tan \alpha = \frac{oh}{hm}[/tex]
tam giác ohn vuông ở h [tex]\rightarrow \tan \beta = \frac{oh}{hn}[/tex]
do đó [tex]\tan \alpha < \tan \beta \rightarrow \alpha < \beta[/tex] (vì hàm tan đồng biến trong [tex](0, \frac{\pi}{2}[/tex])
vậy [tex]\alpha[/tex] là góc nhỏ nhất trong tất cả các góc hợp bởi (p) và (q)
áp dụng vào bài
(d) có vtcp [tex]\vec u(-1, 2, 1)[/tex] và pttq: [tex]\left{\begin{2x+y+1=0}\\{x+z-2=0} [/tex]
(p) có vtpt là [tex]\vec n(2, -1, -2)[/tex]
góc [tex]\sin \alpha = \frac{|\vec u . \vec n|}{|\vec u|.|\vec n|}=\frac{\sqrt 6}{3}[/tex]
[tex]\rightarrow \cos \alpha = \sqrt{1-\frac{6}{9}}=\frac{\sqrt 3}{3}[/tex]
(q) qua (d) có pttq như trên nên có pt chùm dạng:
[tex]m(2x+y+1) + n(x+z-2) = 0, (dk: M^2+n^2 > 0)[/tex]
[tex]\leftrightarrow (2m+n)x+my+nz+(m-2n) =0[/tex]
(vtpt là [tex]\vec t(2m+n, m, n)[/tex])
[tex]\rightarrow \cos \alpha = \frac{|\vec n . \vec t |}{|\vec n|.|\vec t|} =\frac{|3m|}{3.\sqrt{5m^2+2n^2+4mn}}[/tex]
[tex]\frac{|3m|}{3.\sqrt{5m^2+2n^2+4mn}} =\frac{\sqrt 3}{3} \rightarrow m^2 + 2mn + n^2 = 0 \rightarrow (m+n)^2=0 \rightarrow m =-n[/tex]
chọn [tex]m=1 \rightarrow n = -1[/tex]
pt mp (q): [tex]x+y-z+3=0[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
có cách khác, cũng ko dài hơn là mấy.