Cho hình chữ nhật ABCD , K là hình chiếu của B trên AC . M , N lần lượt là trung điểm của AK và CD . Chứng minh : BM vuông góc với MN .
lò lựu đạn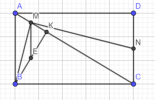
Gọi E là trung điểm BK
[imath]\overrightarrow{BM}=\overrightarrow{BE}+\overrightarrow{EM}=\dfrac{1}2\overrightarrow{BK}-\dfrac{1}2\overrightarrow{AB}[/imath]
[imath]\overrightarrow{MN}=\overrightarrow{BN}-\overrightarrow{BM}[/imath]
[imath]=\overrightarrow{BC}+\dfrac{1}2\overrightarrow{CD}-\dfrac{1}2\overrightarrow{BK}+\dfrac{1}2\overrightarrow{AB}=\overrightarrow{AD}-\dfrac{1}2\overrightarrow{BK}[/imath]
[imath]\overrightarrow{BM}.\overrightarrow{MN}=\dfrac{1}2(\overrightarrow{BK}-\overrightarrow{AB})(\overrightarrow{AD}-\dfrac{1}2\overrightarrow{BK})[/imath]
[imath]\Rightarrow 2\overrightarrow{BM}.\overrightarrow{MN}=\overrightarrow{BK}.\overrightarrow{AD}-\dfrac{1}2BK^2+\dfrac{1}2\overrightarrow{BK}.\overrightarrow{AB}[/imath]
[imath]=\overrightarrow{BK}(\overrightarrow{AC}+\overrightarrow{CD})-\dfrac{1}2BK^2+\dfrac{1}2\overrightarrow{BK}.\overrightarrow{AB}[/imath]
[imath]=\overrightarrow{BK}(\overrightarrow{CD}-\dfrac{1}2\overrightarrow{BK}+\dfrac{1}2\overrightarrow{AB})=\overrightarrow{BK}(-\dfrac{1}2\overrightarrow{AB}-\dfrac{1}2\overrightarrow{BK})=\dfrac{-1}2\overrightarrow{BK}\overrightarrow{AK}=\overrightarrow{0}[/imath]
[imath]\Rightarrow BK\bot MN[/imath]
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Vector
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
