cho đường tròn (O;R) và một điểm S nằm bên ngoài đường tròn.Kẻ các tiếp tuyến SA,SB với đường tròn (A,B là các tiếp điểm)Một đường thẳng đi qua S (không đi qua tâm O) cắt đường tròn (O;R) tại hai điểm M và N với M nằm giữa S và N Gọi H là giao điẻm của SO và AB ;I là trung điểm MN .Hai đường thẳng OI và AB cắt nhau tại E
a) CM IHSE là tứ giác nội tiếp đường tròn
b0 CM SM.SN=SH.SO
c) Cho SO=2R và MN =R căn 3.Tính diện tích tam giác ESM theo R
d) CM EN là tiếp tuyến đường tòn (O)
mọi người giúo em bài trên chi tiết với ạ
em cảm ơn ạ!
01635994996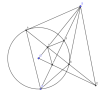
a. Ta có [imath]S A=S B[/imath] (vì [imath]\mathrm{SA}, \mathrm{SB}[/imath] là tiếp tuyến của [imath](\mathrm{O})[/imath] )
[imath]O A=O B(=R)[/imath]
[imath]\rightarrow S O[/imath] là đường trung trực của [imath]A B \rightarrow S O \perp A B \rightarrow \widehat{S H E}=90^{\circ}[/imath]
Do I là trung điểm [imath]\mathrm{MN} \rightarrow \mathrm{OI} \perp \mathrm{MN} \rightarrow \widehat{\mathrm{SIE}}=90^{\circ}[/imath]
Tứ giác [imath]S H I E[/imath] có [imath]\widehat{S H E}[/imath] và [imath]\widehat{S I E}[/imath] cùng nhìn cạnh [imath]\mathrm{SE}[/imath] một góc [imath]90^{\circ}[/imath]
Vậy tứ giác IHSE nội tiếp đường tròn đường kính (SE)
b. Xét [imath]\triangle O H I[/imath] và [imath]\triangle O E S[/imath] có:
[imath]\widehat{O}[/imath] chung;[imath]\widehat{O H I}=\widehat{O E S}[/imath] (cùng bù với [imath]\widehat{SHI}[/imath] )
[imath]\rightarrow \Delta OHI \sim \Delta OES(g . g) \rightarrow \dfrac{O }{OS}=\dfrac{OH}{OE} \rightarrow OI . OE=OH . OS[/imath]
c. Xét [imath]\Delta SAO \perp A, AH \perp SO[/imath] theo hệ thức lượng ta có:
[imath]A O^{2}=OH . OS=R^{2} \rightarrow OI . OE=R^{2}[/imath]
d. Áp dụng định lý Pitogo vào [imath]\Delta OIM[/imath] vuông tại I
[imath]\text { có } O M=R, I M=\dfrac{M N}{2}=\dfrac{R \sqrt{3}}{2} \\\Rightarrow O I^{2}=O M^{2}-I M^{2}=\dfrac{R^{2}}{4} \Rightarrow O I=\dfrac{R}{2}[/imath]
Theo câu c [imath]O I . O E=R^{2}[/imath]
[imath]\Rightarrow O E=\dfrac{R^{2}}{O I}=2 R \\\Rightarrow E I=O E-O I=\dfrac{3 R}{2}[/imath]
Áp dụng định lý pitago vào [imath]\Delta S O I \perp I, S O=2 R, O I=\dfrac{R}{2}[/imath]
[imath]S I^{2}=S O^{2}-O I^{2}=\dfrac{15 R^{2}}{4} \Rightarrow S I=\dfrac{R \sqrt{15}}{2}[/imath]
[imath]\Rightarrow S M=S I-M I=\dfrac{R \sqrt{15}}{2}-\dfrac{R \sqrt{3}}{2}=\dfrac{R(\sqrt{15}-\sqrt{3})}{2}[/imath]
[imath]S_{\Delta E S M}=\dfrac{E I . S M}{2}[/imath]
[imath]=\dfrac{\dfrac{3 R}{2} \cdot \dfrac{R(\sqrt{15}-\sqrt{3})}{2}}{2}[/imath]
[imath]=\dfrac{3 R^{2}(\sqrt{15}-\sqrt{3})}{8} .[/imath]
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em xem thêm tại
Tổng hợp lý thuyết ôn thi HKII lớp 9
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
