[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dạng [imath]1:[/imath] Xác định các đại lượng và trạng thái dao động điều hòa
I, Các định nghĩa:1, Dao động cơ:
Dao động cơ là dao động trong không gian xung quanh một vị trí được gọi là vị trí cân bằng.
[imath]\quad[/imath] Ví dụ: dao động của chiếc lá trên ngọn cây, dao động của màng loa khi phát ra âm thanh.
2, Dao động tuần hoàn:
- Dao động tuần hoàn là dao động có chu kì
- Là dao động mà cứ sau những khoảng thời gian nhất định, trạng thái của vật (vị trí, vận tốc, phương chiều) đều lặp lại như cũ.
[imath]\Rightarrow[/imath] Chu kì [imath]T (s)[/imath] : là khoảng thời gian để vật thực hiện một dao động toàn phần (hoặc khoảng thời gian ngắn nhất để vật trở lại trạng thái như cũ)
[imath]\Rightarrow[/imath] Tần số [imath]f (Hz)[/imath]: Số dao động toàn phần thực hiện được trong [imath]1s[/imath]
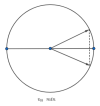
[imath]\quad[/imath] Ví dụ: Con lắc đơn
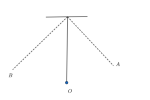
Vật được xem là thực hiện được một dao động điều hòa khi đi được cung tròn [imath]O\to A\to O\to B\to O[/imath]
3, Dao động điều hòa:
- Là dao động mà ly độ của vật được biểu diễn dưới dạng hàm [imath]\sin[/imath] hoặc hàm [imath]\cos[/imath]
Đồ thị biểu diễn ly độ của một vật dao động điều hòa theo thời gian. [imath]x=cos\left(2\pi t\right)[/imath]
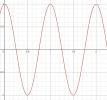
Tổng kết: ta có thể tóm gọn cả ba dao động trong hình minh họa sau:

Hiểu đơn giản chúng là là những tập hợp con, với tập lớn nhất là dao động cơ, trong đó chứa tập con dao động tuần hoàn, và trong nữa sẽ có tập dao động điều hòa. Vậy nếu một vật dao động điều hòa, chắc chắn nó sẽ dao động tuần hoàn, nhưng một vật dao động tuần hoàn thì chưa thể kết luận nó là một dao động điều hòa
Ví dụ: [imath]x=2\cos(\pi t)cm[/imath] là một hàm điều hòa thì sẽ sẽ tuần hoàn luôn
Còn [imath]x=4 +2\cos(\pi t)[/imath] không có dạng của một hàm điều hòa [imath](x=A\cos\left(\omega t+\varphi_0\right))[/imath] nhưng nó là hàm tuần hòa vì nó có chu kì
II, Dao động điều hòa:
1, Phương trình ly độ chuẩn của một dd điều hòa: [imath]x=A\cos\left(\omega t+\varphi_0\right) \ cm[/imath]
Trong đó:
[imath]+ x:[/imath] ly độ dao động (độ dài đại số so với [imath]VTCB[/imath])
[imath]+ A:[/imath] Biên độ dao động (độ lớn ly độ cực đại).
[imath]\quad[/imath] Có thể chứng minh bằng đại số: [imath]|x|=A|\cos\left(\omega t+\varphi_0\right) |\leq A[/imath]
[imath]+ \omega:[/imath] Vận tốc góc [imath](rad/s)[/imath]
[imath]+\varphi_0:[/imath] Pha ban đầu hay pha tại thời điểm chọn làm mốc dao động ([imath]t=0[/imath])
[imath]+\omega t+\varphi_0[/imath]: Pha tại thời điểm [imath]t[/imath]
2, Vận tốc, gia tốc, lực kéo về:
2.1 Vận tốc:
Ta đã học ý nghĩa của đạo hàm trong vật lý
Ta có: [imath]v=x'=-\omega A\sin\left(\omega t+\varphi_0\right)=\omega A\sin\left(\omega t+\varphi_0+\pi\right)=\omega A\cos\left(\omega t+\varphi_0+\dfrac{\pi}{2}\right)[/imath]
Nhận xét:
Nếu xem [imath]v[/imath] là một đại lượng dao động điều hòa thì [imath]v[/imath] có:
+ Biên độ [imath]v_{max}=\omega A[/imath]
+ Vận tốc góc: [imath]\omega_v=\omega_x=\omega[/imath]
+ Pha dao động của [imath]v[/imath] luôn sớm pha hơn pha dao động của [imath]x[/imath] một góc [imath]\dfrac{\pi}{2}[/imath] hay [imath]\varphi_v-\varphi_x=\dfrac{\pi}{2}[/imath]
2.2 Gia tốc
Ta có: [imath]a=v'=x''=-\omega^2 A\cos\left(\omega t+\varphi_0\right)=\omega^2 A\cos\left(\omega t+\varphi_0+\pi\right)=-\omega^2 x[/imath]
Nhận xét:
Tương tự nếu xem [imath]a[/imath] là một đại lượng dao động điều hòa thì [imath]a[/imath] có:
+ Biên độ [imath]a_{max}=\omega^2 A[/imath]
+ Vận tốc góc: [imath]\omega_a=\omega_v=\omega_x=\omega[/imath]
+ Pha dao động của [imath]a[/imath] luôn sớm pha hơn pha dao động của [imath]v[/imath] một góc [imath]\dfrac{\pi}{2}[/imath] hay [imath]\varphi_a-\varphi_v=\dfrac{\pi}{2}[/imath]
+ Từ biểu thức: [imath]a=-\omega^2 x\Rightarrow[/imath] [imath]a[/imath] ngược pha so với [imath]x[/imath]
2.3 Lực kéo về.
Summon định luật II Newton: [imath]F=ma=-m\omega^2x[/imath]
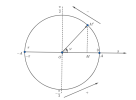
Dấu '-' thể hiện lực [imath]F[/imath] luôn ngược chiều với [imath]x[/imath], quan sát hình vẽ sau:
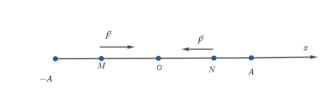
Có thể thấy tại mọi vị trí thì lực [imath]F[/imath] luôn có hướng về [imath]VTCB[/imath] nên nó còn được gọi là lực kéo về (có tác dụng kéo vật về [imath]VTCB[/imath])
3. Tính chất chuyển động:
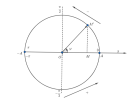
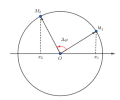
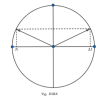
Chú ý: chiều quay của [imath]\varphi[/imath] luôn là chiều ngược chiều kim đồng hồ
- Phần nửa bán cầu trên ứng với pha dương [imath](\varphi >0)[/imath] thì vật chuyển động theo chiều âm hay [imath](v<0)[/imath]
- Phần nửa bán cầu trên ứng với pha âm [imath](\varphi <0)[/imath] thì vật chuyển động theo chiều âm hay [imath](v>0)[/imath]
- Vật chuyển động càng nhanh khi càng gần [imath]VTCB[/imath], càng chậm khi càng gần biên.
Thần chú: Pha âm thì [imath]v[/imath] dương còn pha dương thì [imath]v[/imath] âm.
4. Những vị trí đặc biệt:
+ Biên dương:
- [imath]x_{max}=A, |v| =0, a_{min}=-\omega^2A, F_{min}=-m\omega^2A[/imath]
+ Biên âmL
- [imath]x_{min} = -A,|v| =0, a_{max}=\omega^2A, F_{max}=-m\omega^2A[/imath]
+ VTCB theo chiều dương:
- [imath]x=0, v=|v|=\omega A, a = F =0[/imath]
+ VTCB theo chiều âmL
- [imath]x=0, -v=|v|=\omega A, a=F=0[/imath]
5.Các hệ thức độc lập thời gian:
+ [imath]v=\pm \omega\sqrt{A^2-x^2}[/imath]
+ [imath]\left(\dfrac{x}{A}\right)^2+\left(\dfrac{v}{\omega A}\right)^2=1[/imath] ( vì ([imath]x,v[/imath] vuông pha)
+ [imath]\left(\dfrac{v}{\omega A}\right)^2+\left(\dfrac{a}{\omega^2 A}\right)^2=1[/imath] vì ([imath]v,a[/imath] vuông pha)
6, Đồ thị biểu diễn giữa các đại lượng:
+ [imath]v[/imath] và [imath]x[/imath]
Từ biểu thức [imath]\left(\dfrac{x}{A}\right)^2+\left(\dfrac{v}{\omega A}\right)^2=1[/imath]
Đồ thị biểu diễn giữa [imath]x[/imath] và [imath]v[/imath] là một hình elip với độ dài các trục chính là biên độ của các đại lượng
+ [imath]a[/imath] và [imath]v[/imath]
Từ biểu thức [imath]\left(\dfrac{v}{\omega A}\right)^2+\left(\dfrac{a}{\omega^2 A}\right)^2=1[/imath]
Đồ thị biểu diễn giữa [imath]v[/imath] và [imath]a[/imath] là một hình elip với độ dài các trục chính là biên độ của các đại lượng
+ [imath]a[/imath] và [imath]x[/imath]
Từ biểu thức: [imath]a=-\omega^2 x[/imath]
Vậy đồ thị biểu diễn [imath]a[/imath] theo [imath]x[/imath] là một đoạn thẳng nghịch biến đi qua gốc tọa độ và có hệ số góc [imath]k=-\omega^2[/imath]
Ví dụ: Cho dao động [imath]x=2\cos\left(2\pi t-\dfrac{\pi}{3}\right) \ cm[/imath]
So sánh với phương trình chuẩn [imath]x=A\cos\left(\omega t+\varphi_0\right)[/imath]
[imath]\Rightarrow \begin{cases}A=2 \ cm\\ \omega=2\pi \ rad/s\\ T=\dfrac{2\pi}{\omega}=1s\\f=\dfrac{1}{T}=1 \ Hz\\ \varphi_0=\dfrac{-\pi}{3}rad\\ \varphi_0=2\pi t-\dfrac{\pi}{3}\end{cases}[/imath]
Luyện tập
Câu 1. Li độ của vật dao động điều hòa (với biên độ [imath]\mathrm{A}[/imath], với tần số góc [imath]\omega[/imath] ) có giá trị cực tiểu là
A. [imath]-A[/imath]
B. [imath]+A[/imath]
C. [imath]0[/imath]
D. [imath]-\omega A[/imath]
Câu 2. Li độ của vật dao động điều hỏa (với biên độ [imath]A[/imath],với tần số góc [imath]\omega[/imath] ) có giá trị cực đại là
A. [imath]-\omega A[/imath]
B. [imath]-A[/imath]
C. [imath]+A[/imath]
D. [imath]0[/imath]
Câu 3. Độ lớn li độ của vật dao động điều hòa (vơi biên độ [imath]A[/imath],với tần số góc [imath]\omega[/imath] ) có giá trị cực tiểu là
A. -A
B. [imath]+A[/imath]
C. [imath]0[/imath]
D. [imath]-\omega A[/imath]
Câu 4. Độ lớn li độ của vật dao động điều hòa (vơi biên độ [imath]A[/imath], với tần số góc [imath]\omega[/imath] ) có giá trị cực đại là
A. [imath]-[/imath] A
B. [imath]+A[/imath]
C. [imath]0[/imath]
D. [imath]-\omega A[/imath]
Câu 5. Vận tốc của vật dao động điều hòa có giá trị cực tiểu khi
A. Vật đi qua vị trí cân bẳng theo chiều dương.
B. Vật đến vị trí biên.
C. Lực kéo về triệt tiêu.
D. Vật đi qua vị tri cân bằng theo chiều âm.
Câu 6. Vận tốc của vật dao động điều hòa có giá trị cực đại khi
A. Vật đến vị trí biên.
B. Vật đi qua vị trí cân bằng theo chiều dương.
C. Vật đi qua vị trí cân bằng
D. Vật đi qua vị trí cân bằng theo chiều âm.
Câu 7. Tốc độ (độ lớn của vận tốc) của vật dao động điều hòa có giá trị cực đại khi
A. Vật đi qua vị trí cân bẳng theo chiều dương.
B. Vật đến vị trí biên.
C. Lực kéo về triệt tiêu.
D. Vật đi qua vị trí cân bằng theo chiều âm.
Câu 8. Tốc độ (độ lớn của vận tốc) của vật dao động điều hòa có giá trị cực tiểu khi
A. Vật đi qua vị tri cân bẳng theo chiểu dương.
B. Vật đến vị trí biên.
C. Lực kéo về triệt tiêu.
D. Vật đỉ qua vị trí cân bằng theo chiều âm.
Câu 9. Gia tốc của vật dao động điều hòa (với biên độ [imath]A[/imath] có giá trị cực tiểu khi
A. Vật đến vị trí biên âm [imath]x=-A[/imath]
B. Vật đến vị trí biên dương [imath]x=+A[/imath]
C. Động lượng của vật cực tiểu.
D. Động lượng của vật cực đại.
Câu 10. Gia tốc của vật dao động điều hòa (với biên độ A) có giá trị cực đại khi
A. Vật đến vị trí biên âm [imath]x=-A[/imath].
B. Vật đến vị trí biên dương [imath]x=+A[/imath].
C. Động lượng của vật cụ̣c tiểu.
D. Động lượng của vật cực đại.
Câu 11. Độ lớn gia tốc của vật dao động điều hòa (với biên độ [imath]A[/imath] ) có giá trị cực tiểu khi
A. Vật đí qua vị trí cân bẳng theo chiều dương.
B. Vật đến vị trí biên.
C. Lực kéo về triệt tiêu
D. Vật đi qua vị trí cân bẳng theo chiều âm
Câu 12. Độ lớn gia tốc của vật dao động điều hòa (với biên độ A) có giá trị cực đại khi
A. Vật đi qua vị trí cân bẳng theo chiều dương.
B. Vật đến vị trí biên.
C. Lực kéo về triệt tiêu
D. Vật đi qua vị tri cân bẳng theo chiều âm
1. A
2.C
3.C
4.B
5.D
6.B
7.C
8.B
9.B
10.A
11.C
12.B
2.C
3.C
4.B
5.D
6.B
7.C
8.B
9.B
10.A
11.C
12.B
Bạn đọc tham khảo thêm
[Chuyên đề] Dao động điều hòa - Bài toán thời gian
Last edited: