Vui cười Toán thực tế hay
- Thread starter Kyanhdo
- Ngày gửi
- Replies 45
- Views 4,417
- 22 Tháng sáu 2017
- 2,357
- 4,161
- 589
- 19
- TP Hồ Chí Minh
- THPT Gia Định
Những mẹo tính toán bạn không được dạy ở trường
Như tất cả môn khoa học khác, toán cũng có những bí mật thú vị. Nắm được các quy luật dưới đây, toán có thể sẽ trở thành môn học yêu thích của bạn.
Nhân các số 6, 7, 8, 9 bằng cách sử dụng ngón tay
[TBODY]
[/TBODY]
[TBODY]
[/TBODY]
[TBODY]
[/TBODY]Tính kết quả nhanh của phép nhân 9
[TBODY]
[/TBODY]Nhân nhẩm số có 2 chữ số với 11
[TBODY]
[/TBODY]Cộng trừ hai phân số
[TBODY]
[/TBODY]Nhân hai số có hai chữ số lớn gần bằng 100
[TBODY]
[/TBODY]Nhân số có 2 chữ số với số có 3 chữ số
[TBODY]
[/TBODY]
[TBODY]
[/TBODY]
[TBODY]
[/TBODY]Cách điền dấu lớn hơn, nhỏ hơn
[TBODY]
[/TBODY]Điều kỳ diệu ở phép bình phương các số 1, 11, 111... Đáp án có chữ số đầu và chữ số cuối đều là 1, ở giữa là sự sắp xếp các con số tịnh tiến, mang tính đối xứng.
"Ma thuật" của phép nhân liên quan đến số 8.
Mẹo nhân một số có 2 chữ số (tổng 2 chữ số <10) với 11.
Mẹo nhân một số có nhiều hơn 2 chữ số (tổng hai chữ số liền nhau <10) với 11. Ta giữ nguyên chữ số đầu và chữ số cuối, ở giữa lần lượt là tổng của các chữ số liền nhau theo thứ tự từ trái qua phải.
Bảng cửu chương nhân 9 có một quy luật đặc biệt. Khi sắp xếp các số nhân với 9 theo thứ tự tăng dần và các số nhân với 9 theo thứ tự giảm dần, ta dễ dàng so sánh được đáp án hai bên lần lượt có sự đảo ngược các chữ số.
Phép bình phương số có 2 chữ số bắt đầu bằng số 9 mà không cần máy tính.
Quy luật cộng 2 phân số có tử số là 1.
Mẹo nhân 2 số có dạng: ab x ac (trong đó b+c=10). Hãy thử áp dụng với các phép tính khác: 84 x 86, 92 x 98, 14 x 16.
Như tất cả môn khoa học khác, toán cũng có những bí mật thú vị. Nắm được các quy luật dưới đây, toán có thể sẽ trở thành môn học yêu thích của bạn.
Nhân các số 6, 7, 8, 9 bằng cách sử dụng ngón tay
|
| Phương pháp này được gọi là "Phép nhân kiểu Nga" để thực hiện nhân các số từ 6 đến 9 mà không cần thuộc bảng cửu chương. Trước hết, bạn đánh số cho các ngón tay trên hai bàn tay như hình vẽ, ngón út là 6 và ngón cái là 10. |
|
| Ví dụ, khi muốn thực hiện phép tính 7 x 8, bạn hãy chạm hai ngón tay có số tương ứng vào nhau. |
|
| Sau đó, tổng số ngón tay bên dưới (gồm cả hai ngón chạm vào nhau) là hàng chục. Trong phép tính này, số ngón tay là 5 nên hàng chục là 5 (hoặc 50). Tích số ngón tay phía trên là hàng đơn vị (trong ảnh là 3 x 2 = 6). Sau đó, ghép số hàng chục với hàng đơn vị ta được kết quả là 56. |
|
| Trong bảng cửu chương, bảng nhân 9 tuân theo mỗi quy luật đặc biệt. Để tính bội số của 9, bạn chỉ cần nhớ rằng hàng chục tăng lên từ 0 - 9 và hàng đơn vị giảm dần từ 9 - 0, tổng của chúng luôn bằng 9. |
|
| Cách tính này có 2 bước đơn giản. Đầu tiên, bạn tách số có hai chữ số thành hai phần, số đứng trước là hàng trăm, số đứng sau hàng đơn vị. Tiếp theo, ta cộng hai chữ số với nhau rồi chèn vào giữa tạo thành hàng chục. |
|
| Vẽ hai elip chéo nhau tạo thành hình con bướm. Nhân hai số trong hình elip rồi viết kết quả lên đầu con bướm. Sau đó, trừ (hoặc cộng) hai số đó, ta được tử số của kết quả. Nhân hai mẫu số với nhau tạo thành mẫu số chung (trong hình là 4 x 5 = 20). Ghép tử số với mẫu số chung, ta được phân số mới là kết quả phép tính. |
|
| Phép nhân càng phức tạp khi hai số càng lớn. Tuy nhiên, với phương pháp này, bạn sẽ nhận thấy rằng các số càng lớn càng dễ thực hiện. Trước hết, lấy 100 trừ đi mỗi số, ta được hai số mới. Tiếp đó, bạn tính tổng hai số mới, lấy 100 trừ đi kết quả đó ta được con số hàng nghìn và hàng trăm. Quay trở lại kết quả của hai phép tính đầu tiên, nhân hai số mới với nhau sẽ cho kết quả hàng chục và hàng đơn vị. |
|
| Đây là phương pháp dạy tính phép nhân bằng đường thẳng phổ biến ở Nhật Bản. Với cách tính này, bạn hoàn toàn có thể thực hiện nhân hai số có 2 chữ số hoặc hai số có 3 chữ số với nhau. Bước đầu tiên, ta vẽ các đường thẳng để đại diện cho mỗi chữ số và đan chéo nhau như hình trên. Điều quan trọng là bạn phải luôn nhớ quy tắc từ trái sang phải, kể cả khi vẽ đường thẳng. |
|
| Chia hình vẽ thành các phần đại diện cho hàng nghìn, hàng trăm, hàng chục, hàng đơn vị. |
|
| Từ trái sang phải, bạn đếm các điểm giao nhau trong mỗi phần và viết kết quả. |
|
| Mẹo này dùng để dạy các bé trong các bài tập điền dấu lớn hơn, nhỏ hơn. Chúng ta hãy tưởng tượng dấu lớn hơn (hoặc nhỏ hơn) là hình một cái miệng háu ăn, nó luôn hướng về bên có số lượng lớn hơn |
"Ma thuật" của phép nhân liên quan đến số 8.
Mẹo nhân một số có 2 chữ số (tổng 2 chữ số <10) với 11.
Mẹo nhân một số có nhiều hơn 2 chữ số (tổng hai chữ số liền nhau <10) với 11. Ta giữ nguyên chữ số đầu và chữ số cuối, ở giữa lần lượt là tổng của các chữ số liền nhau theo thứ tự từ trái qua phải.
Bảng cửu chương nhân 9 có một quy luật đặc biệt. Khi sắp xếp các số nhân với 9 theo thứ tự tăng dần và các số nhân với 9 theo thứ tự giảm dần, ta dễ dàng so sánh được đáp án hai bên lần lượt có sự đảo ngược các chữ số.
Phép bình phương số có 2 chữ số bắt đầu bằng số 9 mà không cần máy tính.
Quy luật cộng 2 phân số có tử số là 1.
Mẹo nhân 2 số có dạng: ab x ac (trong đó b+c=10). Hãy thử áp dụng với các phép tính khác: 84 x 86, 92 x 98, 14 x 16.
- 22 Tháng sáu 2017
- 2,357
- 4,161
- 589
- 19
- TP Hồ Chí Minh
- THPT Gia Định
Lịch sử đại số
1. Hình học đã được phát triển ở hình thức tiên đề, còn Số học và Đại số thì không. Tại sao vậy?
Nguyên nhân nằm ở nguồn gốc của chúng. Hình học đã được phát triển bởi người Ai Cập, là kết quả đo đạc đất đai của họ. Vào thế kỉ thứ 7 trước Công nguyên, hình học đã lan truyền từ Ai Cập sang Hi Lạp, nơi nó dần dần phát triển thành một lí thuyết toán học.
Như vậy, hình học là một lí thuyết toán học có nguồn gốc Hi Lạp. Người Hi Lạp đã gắn giá trị lớn cho các chứng minh và vì thế đã phát triển hình học theo hướng tiên đề.
Toán học của những con số của chúng ta có nguồn gốc của nó thuộc về toán học của người Hindu, người Arab và người Babylon. Họ không quan tâm đến việc đưa ra các chứng minh nên toán học của những con số đã được truyền lại cho chúng ta đơn thuần ở dạng một tập hợp những quy tắc tính toán không liên quan với nhau mấy. Xu hướng hiện đại là trình bày tất cả các nghiên cứu toán học theo hình thức tiên đề.
2. Ý nghĩa của từ “arithmetic” là gì?
Từ “arithmetic” (sự tính/số học) có nghĩa là “nghệ thuật tính toán” nên bài học ở trường tiểu học của chúng ta là một tập hợp gồm những lời giải của những bài toán đa dạng và các quy tắc tính toán. Nhưng theo thời gian arithmetic đã biến thành lí thuyết của những con số.
3. Số học là một trừu tượng phải không?
Số học thể hiện những nỗ lực sớm nhất của trí tuệ con người đối với sự trừu tượng. Như vậy, khi chúng ta nói, 2 + 3 = 5, đó là một phát biểu không phải nói về những vật đặc biệt như cái bút chì hay đồng xu, mà về tất cả những vật có thể đếm được vẫn giữ được nhận dạng riêng của chúng.
Ở đây, bản chất của các vật, tức là chúng là cái bút chì hay đồng xu hay cây cối hay bất kì cái gì khác, dù sống hay không sống, vân vân... không còn liên quan nữa, và phát biểu thành ra đúng theo một kiểu chung chung.
Các con số được đặt tên (một, hai, ba,...) và kí hiệu (1, 2, 3,...) và được sử dụng như những vật cụ thể bền bỉ đến mức chúng ta có xu hướng quên mất rằng chúng ta đang giải quyết các khái niệm chứ không phải các vật cụ thể.
4. Phát biểu 2 + 3 = 5 có đúng cho mọi loại vật hay không?
Không. Nếu các vật không giữ được nhận dạng riêng của chúng, thì phát biểu trên có thể không đúng đối với chúng.
Ví dụ, thêm 2 giọt nước vào 3 giọt nước có thể chỉ tạo ra một giọt nước – một giọt nước lớn.
Tương tự, nếu nhốt 2 con hổ và 3 con thỏ chung một chuồng, thì sau một lúc nào đó có thể ta thấy chỉ còn hai con vật thôi – hai con hổ sẽ ăn thịt 3 con thỏ cùng đường mạt lộ kia.
Một ví dụ nữa, một lực bằng 2 đơn vị và một lực khác bằng 3 đơn vị, hai lực cùng tác dụng vào một vật có thể cho hợp lực bằng bất kì giá trị nào nằm giữa 1 và 5 đơn vị lực tùy thuộc vào góc giữa chúng.
Nếu chúng tác dụng ngược chiều nhau, thì tổng của chúng sẽ bằng một đơn vị, còn nếu chúng tác dụng cùng chiều nhau, thì tổng của chúng sẽ bằng 5 đơn vị.
Tuy nhiên, tổng của chúng sẽ bằng 4 đơn vị nếu góc giữa chúng bằng 75,5 độ.
5. Sự mở rộng khái niệm số có nghĩa là gì?
Những con số đầu tiên gắn liền với những vật cụ thể nên khái niệm số ban đầu hạn chế với chỉ những con số nguyên. Các phân số xuất hiện tự nhiên sau đó và sự ra đời của một kí hiệu cho số không là một sự kiện lớn, còn các số âm được thừa nhận lại là một sự miễn cưỡng lớn. Những con số như thế gộp chung lại được gọi là số hữu tỉ. Một lần nữa sự mở rộng này bắt đầu, và đến lượt số vô tỉ và số phức được công nhận. Một số vô tỉ là con số không thể biểu diễn được bằng thương của hai số nguyên. Ví dụ, √2 là một số vô tỉ. Số vô tỉ và số hữu tỉ được gọi chung là số thực. Một số phức là một con số bất kì có dạng a + bi, trong đó a và b là số thực, và i là kí hiệu cho căn bậc hai của trừ một, tức là i2 = - 1.
6. Các số siêu việt là gì?
Những số vô tỉ không bằng căn bậc hai của bất kì phương trình đại số nào được gọi là số siêu việt.
e và π là những số như thế.
e = 2,71828...; π= 3,14159...
các dấu chấm ở cuối có nghĩa là chuỗi số không có kết thúc mà kéo dài đến vô tận. Về các số siêu việt, có một kết quả thú vị do Gelfond chứng minh vào năm 1934 là αβ là siêu việt nếu α là đại lượng đại số khác 0 và khác 1, và β là đại lượng đại số và không phải số hữu tỉ.
Như vậy, 2√3, 3√2, 5√3 là những số siêu việt. Nhưng nếu α và β đều là siêu việt thì không biết αβ có siêu việt hay không. Ví dụ, người ta không rõ ee, ππ hoặc πe có là siêu việt hay không.
Tuy nhiên, eiπ = - 1 là một kết quả rất đẹp.
7. Vì sao đại số được gọi là số học khái quát hóa?
Một ví dụ sẽ làm sáng tỏ.
Ở nhà trường, trẻ em được học rằng nếu lấy bình phương của một con số trừ cho 1, thì nó bằng tích của số liền trước và số liền sau con số đó.
Như vậy, 42 – 1 = (4 + 1) (4 – 1).
52 – 1 = (5 + 1) (5 – 1),
62 – 1 = (6 + 1) (6 – 1).
Rõ ràng mệnh đề trên là đúng nếu ở chỗ 4, 5 hoặc 6, ta thay vào con số bất kì nào khác.
Nếu đưa một kí hiệu mới, ví dụ như x, để biểu diễn một con số bất kì và là một con số không có gì đặc biệt hết, thì mệnh đề trên có thể được viết khái quát như sau
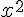– 1 = (x + 1) (x – 1).
Việc đưa thêm vào kí hiệu x là sự khởi đầu của đại số.
8. Sức mạnh của đại số nằm ở đâu?
Đại số có được phần lớn sức mạnh của nó từ việc xử lí bằng kí hiệu với các phần tử, các toán tử và các liên hệ.
Các kí hiệu x, y, z,... được dùng làm các phần tử, phép cộng và phép nhân chủ yếu được dùng làm toán tử, và dấu bằng là liên hệ bình thường kết nối các phần tử.
Như vậy x + x = 2x, và x + y = y + x
cho dù x và y biểu diễn con số nào.
9. Đại số có được khái quát hóa không?
Kí hiệu x, dùng để biểu diễn con số bất kì, có tiềm năng giả định lớn. Trước tiên, nó mang đến các phương trình đại số, cái thống lĩnh địa hạt nghiên cứu lâu đến mức trong khoảng một thế kỉ rưỡi, đại số chỉ là lí thuyết của các phương trình. Sau này x không chỉ hạn chế là những con số mà nó còn được sử dụng để biểu diễn bất kì thực thể nào khác, và các dấu toán tử cho phép cộng và phép nhân đã được phép mang lại những ý nghĩa mới tùy thuộc vào loại thực thể đang được xét đến. Vì thế, thực thể xác định ý nghĩa gắn liền với dấu + và ×. Các vector và ma trận là hai ví dụ quen thuộc của những thực thể như thế. Chúng sẽ được nói tới ở phần sau. Đây là hình ảnh khái quát hóa của cái đại số ban đầu đại diện.
10. Nó khác như thế nào với hình thức ban đầu của đại số?
Trong đại số sơ cấp, các chữ cái kí hiệu cho những con số bình thường, và các dấu toán tử, ví dụ + và ×, kí hiệu cho phép cộng và phép nhân bình thường. Nhưng ở hình thức khái quát hóa, các chữ cái kí hiệu cho thực thể bất kì nào đó, và dấu của toán tử là bất kì quy tắc kết hợp nào có liên quan đến thực thể.
1. Hình học đã được phát triển ở hình thức tiên đề, còn Số học và Đại số thì không. Tại sao vậy?
Nguyên nhân nằm ở nguồn gốc của chúng. Hình học đã được phát triển bởi người Ai Cập, là kết quả đo đạc đất đai của họ. Vào thế kỉ thứ 7 trước Công nguyên, hình học đã lan truyền từ Ai Cập sang Hi Lạp, nơi nó dần dần phát triển thành một lí thuyết toán học.
Như vậy, hình học là một lí thuyết toán học có nguồn gốc Hi Lạp. Người Hi Lạp đã gắn giá trị lớn cho các chứng minh và vì thế đã phát triển hình học theo hướng tiên đề.
Toán học của những con số của chúng ta có nguồn gốc của nó thuộc về toán học của người Hindu, người Arab và người Babylon. Họ không quan tâm đến việc đưa ra các chứng minh nên toán học của những con số đã được truyền lại cho chúng ta đơn thuần ở dạng một tập hợp những quy tắc tính toán không liên quan với nhau mấy. Xu hướng hiện đại là trình bày tất cả các nghiên cứu toán học theo hình thức tiên đề.
2. Ý nghĩa của từ “arithmetic” là gì?
Từ “arithmetic” (sự tính/số học) có nghĩa là “nghệ thuật tính toán” nên bài học ở trường tiểu học của chúng ta là một tập hợp gồm những lời giải của những bài toán đa dạng và các quy tắc tính toán. Nhưng theo thời gian arithmetic đã biến thành lí thuyết của những con số.
3. Số học là một trừu tượng phải không?
Số học thể hiện những nỗ lực sớm nhất của trí tuệ con người đối với sự trừu tượng. Như vậy, khi chúng ta nói, 2 + 3 = 5, đó là một phát biểu không phải nói về những vật đặc biệt như cái bút chì hay đồng xu, mà về tất cả những vật có thể đếm được vẫn giữ được nhận dạng riêng của chúng.
Ở đây, bản chất của các vật, tức là chúng là cái bút chì hay đồng xu hay cây cối hay bất kì cái gì khác, dù sống hay không sống, vân vân... không còn liên quan nữa, và phát biểu thành ra đúng theo một kiểu chung chung.
Các con số được đặt tên (một, hai, ba,...) và kí hiệu (1, 2, 3,...) và được sử dụng như những vật cụ thể bền bỉ đến mức chúng ta có xu hướng quên mất rằng chúng ta đang giải quyết các khái niệm chứ không phải các vật cụ thể.
4. Phát biểu 2 + 3 = 5 có đúng cho mọi loại vật hay không?
Không. Nếu các vật không giữ được nhận dạng riêng của chúng, thì phát biểu trên có thể không đúng đối với chúng.
Ví dụ, thêm 2 giọt nước vào 3 giọt nước có thể chỉ tạo ra một giọt nước – một giọt nước lớn.
Tương tự, nếu nhốt 2 con hổ và 3 con thỏ chung một chuồng, thì sau một lúc nào đó có thể ta thấy chỉ còn hai con vật thôi – hai con hổ sẽ ăn thịt 3 con thỏ cùng đường mạt lộ kia.
Một ví dụ nữa, một lực bằng 2 đơn vị và một lực khác bằng 3 đơn vị, hai lực cùng tác dụng vào một vật có thể cho hợp lực bằng bất kì giá trị nào nằm giữa 1 và 5 đơn vị lực tùy thuộc vào góc giữa chúng.
Nếu chúng tác dụng ngược chiều nhau, thì tổng của chúng sẽ bằng một đơn vị, còn nếu chúng tác dụng cùng chiều nhau, thì tổng của chúng sẽ bằng 5 đơn vị.
Tuy nhiên, tổng của chúng sẽ bằng 4 đơn vị nếu góc giữa chúng bằng 75,5 độ.
5. Sự mở rộng khái niệm số có nghĩa là gì?
Những con số đầu tiên gắn liền với những vật cụ thể nên khái niệm số ban đầu hạn chế với chỉ những con số nguyên. Các phân số xuất hiện tự nhiên sau đó và sự ra đời của một kí hiệu cho số không là một sự kiện lớn, còn các số âm được thừa nhận lại là một sự miễn cưỡng lớn. Những con số như thế gộp chung lại được gọi là số hữu tỉ. Một lần nữa sự mở rộng này bắt đầu, và đến lượt số vô tỉ và số phức được công nhận. Một số vô tỉ là con số không thể biểu diễn được bằng thương của hai số nguyên. Ví dụ, √2 là một số vô tỉ. Số vô tỉ và số hữu tỉ được gọi chung là số thực. Một số phức là một con số bất kì có dạng a + bi, trong đó a và b là số thực, và i là kí hiệu cho căn bậc hai của trừ một, tức là i2 = - 1.
6. Các số siêu việt là gì?
Những số vô tỉ không bằng căn bậc hai của bất kì phương trình đại số nào được gọi là số siêu việt.
e và π là những số như thế.
e = 2,71828...; π= 3,14159...
các dấu chấm ở cuối có nghĩa là chuỗi số không có kết thúc mà kéo dài đến vô tận. Về các số siêu việt, có một kết quả thú vị do Gelfond chứng minh vào năm 1934 là αβ là siêu việt nếu α là đại lượng đại số khác 0 và khác 1, và β là đại lượng đại số và không phải số hữu tỉ.
Như vậy, 2√3, 3√2, 5√3 là những số siêu việt. Nhưng nếu α và β đều là siêu việt thì không biết αβ có siêu việt hay không. Ví dụ, người ta không rõ ee, ππ hoặc πe có là siêu việt hay không.
Tuy nhiên, eiπ = - 1 là một kết quả rất đẹp.
7. Vì sao đại số được gọi là số học khái quát hóa?
Một ví dụ sẽ làm sáng tỏ.
Ở nhà trường, trẻ em được học rằng nếu lấy bình phương của một con số trừ cho 1, thì nó bằng tích của số liền trước và số liền sau con số đó.
Như vậy, 42 – 1 = (4 + 1) (4 – 1).
52 – 1 = (5 + 1) (5 – 1),
62 – 1 = (6 + 1) (6 – 1).
Rõ ràng mệnh đề trên là đúng nếu ở chỗ 4, 5 hoặc 6, ta thay vào con số bất kì nào khác.
Nếu đưa một kí hiệu mới, ví dụ như x, để biểu diễn một con số bất kì và là một con số không có gì đặc biệt hết, thì mệnh đề trên có thể được viết khái quát như sau
Việc đưa thêm vào kí hiệu x là sự khởi đầu của đại số.
8. Sức mạnh của đại số nằm ở đâu?
Đại số có được phần lớn sức mạnh của nó từ việc xử lí bằng kí hiệu với các phần tử, các toán tử và các liên hệ.
Các kí hiệu x, y, z,... được dùng làm các phần tử, phép cộng và phép nhân chủ yếu được dùng làm toán tử, và dấu bằng là liên hệ bình thường kết nối các phần tử.
Như vậy x + x = 2x, và x + y = y + x
cho dù x và y biểu diễn con số nào.
9. Đại số có được khái quát hóa không?
Kí hiệu x, dùng để biểu diễn con số bất kì, có tiềm năng giả định lớn. Trước tiên, nó mang đến các phương trình đại số, cái thống lĩnh địa hạt nghiên cứu lâu đến mức trong khoảng một thế kỉ rưỡi, đại số chỉ là lí thuyết của các phương trình. Sau này x không chỉ hạn chế là những con số mà nó còn được sử dụng để biểu diễn bất kì thực thể nào khác, và các dấu toán tử cho phép cộng và phép nhân đã được phép mang lại những ý nghĩa mới tùy thuộc vào loại thực thể đang được xét đến. Vì thế, thực thể xác định ý nghĩa gắn liền với dấu + và ×. Các vector và ma trận là hai ví dụ quen thuộc của những thực thể như thế. Chúng sẽ được nói tới ở phần sau. Đây là hình ảnh khái quát hóa của cái đại số ban đầu đại diện.
10. Nó khác như thế nào với hình thức ban đầu của đại số?
Trong đại số sơ cấp, các chữ cái kí hiệu cho những con số bình thường, và các dấu toán tử, ví dụ + và ×, kí hiệu cho phép cộng và phép nhân bình thường. Nhưng ở hình thức khái quát hóa, các chữ cái kí hiệu cho thực thể bất kì nào đó, và dấu của toán tử là bất kì quy tắc kết hợp nào có liên quan đến thực thể.
- 22 Tháng sáu 2017
- 2,357
- 4,161
- 589
- 19
- TP Hồ Chí Minh
- THPT Gia Định
QUY TRÌNH GIẢI BÀI TOÁN THỰC TIỄN
Vận dụng toán học vào thực tiễn là một trong những yêu cầu quan trọng trong các mục tiêu giáo dục môn Toán bậc trung học.
Việc thường xuyên vận dụng toán học vào thực tế sẽ giúp học sinh nhìn thấy những khía cạnh toán học ở các tình huống thường gặp trong cuộc sống, tăng cường khả năng giải quyết các vấn đề trong cuộc sống bằng tư duy toán học, giúp tập luyện thói quen làm việc khoa học, nâng cao ý thức tối ưu hóa trong lao động…
Đây là những phẩm chất quan trọng đối với người lao động trong xã hội ngày nay. Để làm được điều này học sinh phải có khả năng thu nhận được thông tin toán học từ tình huống thực tế ban đầu, chuyển đổi thông tin giữa thực tế và toán học, thiết lập được mô hình toán học từ tình huống thực tế.
Đó không phải là công việc dễ dàng nếu không thực hiện theo một trình tự nhất định. Do đó khi dạy cho học sinh giải các bài toán thực tiễn giáo viên nên hưỡng dẫn cho học sinh giải theo các bước.
Trong sách giáo khoa môn Toán ở THCS, quy trình giải các bài toán thực tế không được đưa vào một cách tường minh mà chỉ được đưa vào trong trường hợp cụ thể đó là quy trình giải bài toán bằng cách lập phương trình hoặc hệ phương trình (Toán 8 – toán 9) gồm 3 bước đó là:
Bước 1: Lập phương trình: Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số; biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết; lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.
Với những bài toán tổng hợp, có nội dung thực tiễn khác giáo viên cũng cần trang bị cho học sinh quy trình để giải bài toán thực tế theo các bước sau:
Bước 1: Đọc, hiểu nội dung bài toán thực tiễn đã cho
Bước 2: Toán học hóa bài toán thực tiễn đã cho
Bước 3: Dùng kiến thức toán đã được học, giải bài toán đã được toán học hóa
Bước 4: Quay lại tình huống ban đầu trả lời.
Đối với các bài toán của PISA, người ta sử dụng quy trình Toán học hóa để giải các bài toán đó. Quy trình này gồm có 5 bước:
Bước 1: Bắt đầu từ một vấn đề thực tế
Bước 2: Diễn đạt lại nội dung vấn đề được đặt ra theo các khái niệm toán học và xác định các kiến thức toán học có liên quan.
Bước 3: Chuyển bài toán thực tế thành bài toán đại diện trung thực cho hoàn cảnh thực tế thông qua quá trình đặt giả thuyết, tổng quát, hình thức hóa.
Bước 4: Giải quyết bài toán bằng phương pháp toán học
Bước 5: Làm cho lời giải có ý nghĩa của hoàn cảnh thực tiễn bao gồm xác định những hạn chế của lời giải.
Ví dụ: “Giá sách” (Trích từ tài liệu PISA) (Sau khi học xong bài Bội và ước toán 6 giáo viên có thể đưa ra bài toán).
Để làm được một giá sách người thợ mộc cần các bộ phận sau: 4 tấm gỗ dài, 6 tấm gỗ ngắn, 12 cái kẹp nhỏ, 2 cái kẹp lớn và 14 cái ốc vít.
Người thợ mộc đang có 26 tấm gỗ dài, 33 tấm gỗ ngắn, 200 kẹp nhỏ, 20 kẹp lớn, 510 cái ốc vít. Câu hỏi: Người thợ mộc có thể làm được nhiều nhất là bao nhiêu cái giá sách?
Để giải quyết bài toán trên ta có thể tiến hành theo quy trình sau:
Bước 1: Bắt đầu từ một vấn đề thực tế
Vấn đề đặt ra là tìm số giá sách người thợ mộc có thể làm được. Câu hỏi được đặt trong bối cảnh thế giới thực và sự thực tế này là xác thực tuy nhiên ít phức tạp hơn so với hầu hết các vấn đề thực tế do hầu như không có thông tin không liên quan hoặc dư thừa được đưa ra.
Bước 2: Diễn đạt lại nội dung vấn đề được đặt ra theo các khái niệm toán học và xác định các kiến thức toán học có liên quan.
Một cái giá sách cần số tấm gỗ dài, tấm gỗ ngắn, kẹp nhỏ, kẹp lớn, ốc vít theo thứ tự là: 4, 6, 12, 2 và 14, Theo đề bài số tấm gỗ dài, tấm gỗ ngắn, kẹp nhỏ, kẹp lớn, ốc vít theo thứ tự là: 26, 33, 200, 20, 510.
GV có thể hướng dẫn HS tóm tắt theo bảng sau:
[TBODY]
[/TBODY]Bước 3: Chuyển bài toán thực tế thành bài toán đại diện trung thực cho hoàn cảnh thực tế thông qua quá trình đặt giả thuyết, tổng quát, hình thức hóa.
Cần chuyển câu hỏi: “Người thợ mộc có thể làm được bao nhiêu cái giá sách?” thành một vấn đề toán học. Đó có thể là tìm bội số lớn nhất của tập đầu tiên (4, 6, 12, 2 và 14) thỏa mãn tập còn lại (26, 33, 200, 20, 510).
Học sinh sẽ có mô hình toán học của bài toán thực tế trên thực chất là đi tìm k là số tự nhiên lớn nhất (k khác 0) đồng thời thỏa mãn các điều kiện: 4k nhỏ hơn hoặc bằng 26; 6k nhỏ hơn hoặc bằng
33; 12k nhỏ hơn hoặc bằng 200; 2k nhỏ hơn hoặc bằng 20; 14k nhỏ hơn hoặc bằng 510
Bước 4: Giải quyết bài toán
Cách 1: Học sinh trung bình có thể giải bài toán bằng cách liệt kê theo bảng dưới đây:
[TBODY]
[/TBODY]Tiếp tục liệt kê đến khi thấy một con số vượt ra ngoài giá trị của tập còn lại. Ở bài toán trên, học sinh sẽ thấy rằng nếu làm 6 giá sách thì cần có 36 tấm gỗ ngắn trong khi theo dữ kiện đề bài ta chỉ có 33 tấm gỗ ngắn. Vậy người thợ mộc có thể làm được nhiều nhất là 5 giá sách.
Tuy nhiên cách này khá dài dòng và nếu số liệu đưa ra là những con số rất lớn thì cách làm này không khả thi. Vậy còn cách làm nào khác không?
Cách 2: Học sinh khá giỏi có thể giải quyết bài toán rất nhanh dựa theo sự ước tính: 26/4 = 6 + số còn lại; 33/6 = 5 + số còn lại, các tỉ số 200/12; 20/2 ; 510/14 đều lớn hơn hoặc bằng 10. Vậy câu trả lời là 5.
Bước 5: Làm cho lời giải có ý nghĩa của hoàn cảnh thực tiễn bao gồm xác định cả những hạn chế của lời giải
Ý nghĩa thực tế của bài toán là với các thành phần được liệt kê ở đầu bài người thợ có thể làm được 5 cái giá sách tuy nhiên dựa trên việc quan sát số liệu đã được liệt kê ở cách 1 ta nhận thấy rằng chỉ cần có thêm 3 tấm gỗ ngắn, ta có thể đóng thêm được một cái giá sách nữa.
Và trên thực tế ta có thể cưa 2 tấm gỗ dài còn thừa thành 3 tấm gỗ ngắn chẳng hạn. Bài tập trên giúp học sinh có vận kiến thức toán học vào thực tế một cách rất tự nhiên. Đó là những kiến thức về tìm bội số của một số với điều kiện cho trước.
Hơn nữa bài toán cũng cho thấy một khía cạnh rất thực tế khi làm việc là xảy ra vấn đề thừa thiếu nguyên vật liệu trong sản xuất, người lao động phải xem xét đánh giá lựa chọn phương án để có được hiệu quả kinh tế cao nhất.
(Sưu tầm)
Vận dụng toán học vào thực tiễn là một trong những yêu cầu quan trọng trong các mục tiêu giáo dục môn Toán bậc trung học.
Việc thường xuyên vận dụng toán học vào thực tế sẽ giúp học sinh nhìn thấy những khía cạnh toán học ở các tình huống thường gặp trong cuộc sống, tăng cường khả năng giải quyết các vấn đề trong cuộc sống bằng tư duy toán học, giúp tập luyện thói quen làm việc khoa học, nâng cao ý thức tối ưu hóa trong lao động…
Đây là những phẩm chất quan trọng đối với người lao động trong xã hội ngày nay. Để làm được điều này học sinh phải có khả năng thu nhận được thông tin toán học từ tình huống thực tế ban đầu, chuyển đổi thông tin giữa thực tế và toán học, thiết lập được mô hình toán học từ tình huống thực tế.
Đó không phải là công việc dễ dàng nếu không thực hiện theo một trình tự nhất định. Do đó khi dạy cho học sinh giải các bài toán thực tiễn giáo viên nên hưỡng dẫn cho học sinh giải theo các bước.
Trong sách giáo khoa môn Toán ở THCS, quy trình giải các bài toán thực tế không được đưa vào một cách tường minh mà chỉ được đưa vào trong trường hợp cụ thể đó là quy trình giải bài toán bằng cách lập phương trình hoặc hệ phương trình (Toán 8 – toán 9) gồm 3 bước đó là:
Bước 1: Lập phương trình: Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số; biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết; lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.
Với những bài toán tổng hợp, có nội dung thực tiễn khác giáo viên cũng cần trang bị cho học sinh quy trình để giải bài toán thực tế theo các bước sau:
Bước 1: Đọc, hiểu nội dung bài toán thực tiễn đã cho
Bước 2: Toán học hóa bài toán thực tiễn đã cho
Bước 3: Dùng kiến thức toán đã được học, giải bài toán đã được toán học hóa
Bước 4: Quay lại tình huống ban đầu trả lời.
Đối với các bài toán của PISA, người ta sử dụng quy trình Toán học hóa để giải các bài toán đó. Quy trình này gồm có 5 bước:
Bước 1: Bắt đầu từ một vấn đề thực tế
Bước 2: Diễn đạt lại nội dung vấn đề được đặt ra theo các khái niệm toán học và xác định các kiến thức toán học có liên quan.
Bước 3: Chuyển bài toán thực tế thành bài toán đại diện trung thực cho hoàn cảnh thực tế thông qua quá trình đặt giả thuyết, tổng quát, hình thức hóa.
Bước 4: Giải quyết bài toán bằng phương pháp toán học
Bước 5: Làm cho lời giải có ý nghĩa của hoàn cảnh thực tiễn bao gồm xác định những hạn chế của lời giải.
Ví dụ: “Giá sách” (Trích từ tài liệu PISA) (Sau khi học xong bài Bội và ước toán 6 giáo viên có thể đưa ra bài toán).
Để làm được một giá sách người thợ mộc cần các bộ phận sau: 4 tấm gỗ dài, 6 tấm gỗ ngắn, 12 cái kẹp nhỏ, 2 cái kẹp lớn và 14 cái ốc vít.
Người thợ mộc đang có 26 tấm gỗ dài, 33 tấm gỗ ngắn, 200 kẹp nhỏ, 20 kẹp lớn, 510 cái ốc vít. Câu hỏi: Người thợ mộc có thể làm được nhiều nhất là bao nhiêu cái giá sách?
Để giải quyết bài toán trên ta có thể tiến hành theo quy trình sau:
Bước 1: Bắt đầu từ một vấn đề thực tế
Vấn đề đặt ra là tìm số giá sách người thợ mộc có thể làm được. Câu hỏi được đặt trong bối cảnh thế giới thực và sự thực tế này là xác thực tuy nhiên ít phức tạp hơn so với hầu hết các vấn đề thực tế do hầu như không có thông tin không liên quan hoặc dư thừa được đưa ra.
Bước 2: Diễn đạt lại nội dung vấn đề được đặt ra theo các khái niệm toán học và xác định các kiến thức toán học có liên quan.
Một cái giá sách cần số tấm gỗ dài, tấm gỗ ngắn, kẹp nhỏ, kẹp lớn, ốc vít theo thứ tự là: 4, 6, 12, 2 và 14, Theo đề bài số tấm gỗ dài, tấm gỗ ngắn, kẹp nhỏ, kẹp lớn, ốc vít theo thứ tự là: 26, 33, 200, 20, 510.
GV có thể hướng dẫn HS tóm tắt theo bảng sau:
| Cho biết | Tên vật liệu | Số tấm gỗ dài | Số tấm gỗ ngắn | Số kẹp nhỏ | Số kẹp lớn | Số ốc vít |
| Vật liệu cần thiết để làm một cái giá sách | 4 | 6 | 12 | 2 | 14 | |
| Vật liệu đang có | 26 | 33 | 200 | 20 | 510 | |
| Yêu cầu | Tìm số cái giá sách người thợ có thể làm được nhiều nhất từ vật liệu đã có |
Cần chuyển câu hỏi: “Người thợ mộc có thể làm được bao nhiêu cái giá sách?” thành một vấn đề toán học. Đó có thể là tìm bội số lớn nhất của tập đầu tiên (4, 6, 12, 2 và 14) thỏa mãn tập còn lại (26, 33, 200, 20, 510).
Học sinh sẽ có mô hình toán học của bài toán thực tế trên thực chất là đi tìm k là số tự nhiên lớn nhất (k khác 0) đồng thời thỏa mãn các điều kiện: 4k nhỏ hơn hoặc bằng 26; 6k nhỏ hơn hoặc bằng
33; 12k nhỏ hơn hoặc bằng 200; 2k nhỏ hơn hoặc bằng 20; 14k nhỏ hơn hoặc bằng 510
Bước 4: Giải quyết bài toán
Cách 1: Học sinh trung bình có thể giải bài toán bằng cách liệt kê theo bảng dưới đây:
| Tên vật liệu | Số tấm gỗ dài | Số tấm gỗ ngắn | Số kẹp nhỏ | Số kẹp lớn | Số ốc vít |
| Vật liệu cần thiết để làm một cái giá sách | 4 | 6 | 12 | 2 | 14 |
| Vật liệu cần thiết để làm hai cái giá sách | 8 | 12 | 24 | 4 | 28 |
| Vật liệu cần thiết để làm ba cái giá sách | 12 | 18 | 36 | 6 | 42 |
| Vật liệu cần thiết để làm bốn cái giá sách | 16 | 24 | 48 | 8 | 56 |
| Vật liệu cần thiết để làm năm cái giá sách | 20 | 30 | 60 | 10 | 70 |
| Vật liệu cần thiết để làm sáu cái giá sách | 24 | 36 | 72 | 12 | 84 |
| So với vật liệu đang có | 26 | 33 | 200 | 20 | 510 |
Tuy nhiên cách này khá dài dòng và nếu số liệu đưa ra là những con số rất lớn thì cách làm này không khả thi. Vậy còn cách làm nào khác không?
Cách 2: Học sinh khá giỏi có thể giải quyết bài toán rất nhanh dựa theo sự ước tính: 26/4 = 6 + số còn lại; 33/6 = 5 + số còn lại, các tỉ số 200/12; 20/2 ; 510/14 đều lớn hơn hoặc bằng 10. Vậy câu trả lời là 5.
Bước 5: Làm cho lời giải có ý nghĩa của hoàn cảnh thực tiễn bao gồm xác định cả những hạn chế của lời giải
Ý nghĩa thực tế của bài toán là với các thành phần được liệt kê ở đầu bài người thợ có thể làm được 5 cái giá sách tuy nhiên dựa trên việc quan sát số liệu đã được liệt kê ở cách 1 ta nhận thấy rằng chỉ cần có thêm 3 tấm gỗ ngắn, ta có thể đóng thêm được một cái giá sách nữa.
Và trên thực tế ta có thể cưa 2 tấm gỗ dài còn thừa thành 3 tấm gỗ ngắn chẳng hạn. Bài tập trên giúp học sinh có vận kiến thức toán học vào thực tế một cách rất tự nhiên. Đó là những kiến thức về tìm bội số của một số với điều kiện cho trước.
Hơn nữa bài toán cũng cho thấy một khía cạnh rất thực tế khi làm việc là xảy ra vấn đề thừa thiếu nguyên vật liệu trong sản xuất, người lao động phải xem xét đánh giá lựa chọn phương án để có được hiệu quả kinh tế cao nhất.
(Sưu tầm)
- 22 Tháng sáu 2017
- 2,357
- 4,161
- 589
- 19
- TP Hồ Chí Minh
- THPT Gia Định
Các phương pháp ước đạt – ước lượng
Trong cuộc sống, công việc tính toán là hằng ngày, hằng giờ trong mỗi chúng ta. Thật vậy, nó là công cụ không thể thiếu để chúng ta giải quyết các vấn đề trong đời sống.
Trong nhà trường việc học và giải các bài toán sẽ cho chúng ta một con số chính xác nhưng khi ứng dụng ngoài thực tế thì những con số ấy chỉ là tương đối. Không phải lúc nào và trong mọi trường hợp chúng ta đều có sẵn dụng cụ đo đạc, vậy thì chúng ta phải làm sao đây? Kỹ năng Ước đạc – ước lượng sẽ giúp chúng ta lúc này.
1) Ước đạc là gì?
2) Ước đạc khoảng cách:
a) Phương pháp bước đôi:
b) Phương pháp bằng mắt thường:
b) Phương pháp dùng vận tốc của âm thanh:
Ta tính 330m/s x 9 = 2.970 m.
Vậy sấm chớp cách xa ta khoảng 3 km.
c) Phương pháp bằng xe đạp:
Nguyên tắc chính được dùng trong hầu hết phương pháp ước đạt chiều cao là dựa vào nguyên tắc tam giác đồng dạng. Các phương pháp sau đây là những phương pháp dễ thực hiện và có độ chính xác cao nhất.
a) Phương pháp dùng gậy – nằm trên mặt đất:
Phương pháp này đòi hỏi phải có một khoảng đất trống vừa đủ rộng. Các bước thực hiện như sau:
b) Phương pháp dùng gậy và bóng nắng:
Nếu có ánh mặt trời, ta đo chiều cao bằng cách cắm một cây gậy xuống đất, đo chiều dài của chiều dài của bóng cây và bóng gậy in trên mặt đất. Gọi:
c) Phương pháp “Cách ngắm của Họa sĩ”:
4) Ước đạc chiều rộng:
a) Phương pháp hai tam giác vuong bằng nhau:
b) Phương pháp tam giác đồng dạng:
4) Ước đạc chiều sâu:
Khi đứng ở một độ cao ở một nơi nào đó, thì để muốn biết chiều sâu từ nơi ta đúng đến mặt đất ta chỉ cần tảh một vật nặng rơi tự do (ví dụ: lon nước ngọt, thùng nhôm,…) khi chạm đất sẽ gây tiếng động. Chúng ta chỉ cần tính thời gian rơi tự do là bao nhiêu rồi áp dụng công thức chúng ta sẽ biết được độ cao cần tìm.
Công thức: H = g s2
Với: H : Độ cao (chiều sâu) cần tìm (m)
s : thời gian rơi tự do.
g = 9,8 m/s2 – gia tốc rơi tự do.
5) Cách tạo một góc vuông trên mặt đất:
Có rất nhiều cách để tạo một góc vuông 900 trên mặt đất. Ở đây xin giới thiệu đến các bạn 2 phương pháp cơ bản để tạo góc vuông với những dụng cụ thô sơ (dây, gậy gỗ, phấn…).
Thí dụ muốn vẽ một đường thẳng vuông góc với đoạn AB tại điểm B, ta có 2 phương pháp cơ bản sau:
a) Phương pháp 1 (đường thẳng & tam giác):
b) Phương pháp 2 (tam giác & đường tròn):
1) Ước lượng diện tích:
Đo chiều dài
Trong cuộc sống, công việc tính toán là hằng ngày, hằng giờ trong mỗi chúng ta. Thật vậy, nó là công cụ không thể thiếu để chúng ta giải quyết các vấn đề trong đời sống.
Trong nhà trường việc học và giải các bài toán sẽ cho chúng ta một con số chính xác nhưng khi ứng dụng ngoài thực tế thì những con số ấy chỉ là tương đối. Không phải lúc nào và trong mọi trường hợp chúng ta đều có sẵn dụng cụ đo đạc, vậy thì chúng ta phải làm sao đây? Kỹ năng Ước đạc – ước lượng sẽ giúp chúng ta lúc này.
1) Ước đạc là gì?
- Ước đạc là dùng phương pháp hình học, bằng những khí cụ thô sơ để đo đạc một vật thể có thật nào đó trong thiên nhiên mà chỉ cho ta kết quả tương đối. Sai suất không quá 10%.
- Để có được kỹ năng ước đạc tương đối chính xác nhất thì đòi hỏi các bạn phải tập luyện thường xuyên. Điều này sẽ giúp cho các bạn sẽ quen mắt, quen tay và kỹ năng ước đạt nhạy bén hơn.
- Trước khi bạn thực hành ước đạc thì bạn phải biết thật rõ các số đo cá nhân. Các số đo cá nhân như: Chiều cao của mình từ chân đến đầu, đến mắt, đến vai…, chiều dài một sải tay, chiều dài 1 cánh tay, 1 gang tay, một ngón tay, 1 gang chân, 1 bước chân thường, 1 bước nhảy, 1 bước chạy…
2) Ước đạc khoảng cách:
a) Phương pháp bước đôi:
- Tập đi nhiều lần trong một khoảng cách ấn định (100m), cứ 2 bước đếm 1 lần.
- Sau khi bước trung bình và đều qua nhiều lần, chúng ta ghi nhận số bước có nhiều lần trùng với nhau.
- Lấy 100m chia cho số bước chúng ta sẽ có đáp số.
- Ví dụ:
b) Phương pháp bằng mắt thường:
- Khi ước đạc khoảng cách bằng mắt thường (không cận thị, viễn thị, loạn thị) Trong trường hợp thời tiết tốt không có sương mù, phải đầy đủ ánh sáng, chúng ta có thể thấy:
- Đồ vật trông có vẻ gần hơn thực tế khi quan sát bằng mắt:
- – Vào lúc trời trông sáng.
- – Khi mẵt trời ở phía sau lưng.
- – Qua một khoảng cách có nước.
- – Qua một thung lũng.
- – Qua một dãi tuyết.
- – Trên cánh đồng.
- – Qua núi đồi trập trùng.
- – Trên một đường tuyến ở phía chân trời.
- Đồ vật trông có vẻ xa hơn thực tế khi:
- – Khi nhìn ở tư thế quỳ hay nằm.
- – Người mà ta nhìn cũng quỳ.
- – Đồ vật có cùng màu với bối cảnh.
- – Được nhìn trong ngày sương mù, ảm đạm.
- – Nhìn dọc theo một con phố hay một đại lộ.
- – Có quần hơi nước do sức nóng gây nên.
- Chúng ta biết rằng, cứ mỗi giây âm thanh truyền đi với vận tốc 330m/s .Muốn tính khoảng
- cách từ chỗ phát ra tiếng động đến chỗ ta đứng (với điều kiện bạn phải thấy được nơi phát ra tiếng động).
- Chúng ta tính từ lúc phát ra tiếng động (dưới các hình thức: sấm, chớp, bắn súng…) cho đến lúc chúng ta nghe được tiếng động là bao nhiêu giây. Ta lấy số giây đó nhân với 330m/s là ra khoảng cách.
- Muốn tính số giây ta tập đếm: Ba trăm lẻ một, ba trăm lẻ hai… (301, 302,…).
- Ví dụ:
Ta tính 330m/s x 9 = 2.970 m.
Vậy sấm chớp cách xa ta khoảng 3 km.
c) Phương pháp bằng xe đạp:
- Các bạn lấy một mảnh vải trắng cột vào bánh xe trước, cứ mỗi vòng lăn (tuy theo kích cỡ
- của bánh xe) ta có một số đo. Lấy số đo đó nhân với chu vi bánh xe ta sẽ có khoảng cách cần tìm. Thường thì chu vi bánh xe đạp 650 là 1,90m.
- Lưu ý: Chúng ta cũng có thể tính toán theo số vòng đạp của pedale (bàn đạp). Ta phải biết trước, nếu đạp đều thì 1 vòng đạp của pedale sẽ đi được bao xa? Sau đó thì ta chỉ việt là lấy khoảng cách một vòng đạp nhân với số vòng đã đạp một khoảng cách từ điềm này đến điểm kia. Ta sẽ có khoảng cách giữa 2 điểm ấy là bao nhiêu mét.
Nguyên tắc chính được dùng trong hầu hết phương pháp ước đạt chiều cao là dựa vào nguyên tắc tam giác đồng dạng. Các phương pháp sau đây là những phương pháp dễ thực hiện và có độ chính xác cao nhất.
a) Phương pháp dùng gậy – nằm trên mặt đất:
Phương pháp này đòi hỏi phải có một khoảng đất trống vừa đủ rộng. Các bước thực hiện như sau:
- – Cắm 1 cây gậy có chiều cao là “h” cách gốc cây 1 khoảng sao cho có thể lấy số đo.
- – Nằm xuống và ngắm sao cho ngọn cây trùng với đỉnh của gậy. Bây giờ, mắt, đỉnh gậy và ngọn cây nằm trên cùng một đường thẳng.
- – Gọi đoạn từ vị trí đặt mắt đến gốc cây là “D, từ mắt đến nơi cắm gậy là “d”.
- – Bây giờ ta có thể tính chiều cao H của cây, bằng công thức sau:
b) Phương pháp dùng gậy và bóng nắng:
Nếu có ánh mặt trời, ta đo chiều cao bằng cách cắm một cây gậy xuống đất, đo chiều dài của chiều dài của bóng cây và bóng gậy in trên mặt đất. Gọi:
- – H là chiều cao của cây muốn đo.
- – B là chiều dài của bóng cây.
- – h là chiều cao của gậây.
- – b là chiều dài của bóng gậây.
- Ta có công thức sau:
- H = h*B/b
c) Phương pháp “Cách ngắm của Họa sĩ”:
- – Đặt dưới chân mục tiêu cần đo một cây gậy chuẩn (hay một người đứng ngay chỗ mục tiêu) ma ta đã biết rõ chiều cao.
- – Đứng cách xa mục tiêu một khoảng cách gấp 2 – 3 lần chiều cao phỏng đoán của mục tiêu
- – Cầm một cây que hoặc một cây bút dang thẳng tay ra đằng trước.
- – Bấm ngón tay trên que để ghi dấu chỗ trên mặt đất.
- – Xong chúng ta đo ướm dần lên xem mục tiêu cao hơn vật chuẩn mấy lần.
- – Nhân chiều cao của vật chuẩn với số lần đó thì ta có chiếu cao mục tiêu.
4) Ước đạc chiều rộng:
a) Phương pháp hai tam giác vuong bằng nhau:
- – Ta chọn một điểm móc A bên kia sát mép bên bờ sông, đối diện bờ sông bên này ta đóng một cọc B sát bờ.
- – Từ B ta xoay 1 góc 900 rồi đo đến 1 điểm bất kỳ để đóng cọc C, kéo dài BC chọn điểm D sao cho CB = CD.
- – Tại D kẻ một tia Dx vuông góc với BD (góc vuông tại D)
- – Trên tia Dx xác định điểm E sao cho A, C, E thẳng hàng.
- – Ta có: Hai tam giác vuông ÑABC = ÑEDC. Nên AB = ED.
- – Đo ED chính là khoản cách AB (chiều rộng bờ sông) cần tìm.
b) Phương pháp tam giác đồng dạng:
- – Chọn một điểm mốc P sát bên kia bờ sông, đối diện sát bờ sông bên này đóng một cọc A. Từ PA ta nối dài đóng một cọc tiêu C.
- – Kẻ tia Ax vuông góc với PC tại A, trên tia Ax đóng tiêu cọc B.
- – Kẻ tia Cy vuông góc với PC tại C, trên tia Cy xác định cọc tiêu D sao cho P, B, D thẳng hàng.
- – Ta có tam giác ÑPAB đồng dạng với ÑPCD
- PC = CD => PC – PA = CD – AB
- PA .. AB ………PA …………AB
- Vì PC – PA = AC nên AC = CD – AB
- …………………………….PA….. AB
- Do đó PA = AC * AB
- ………………CD – AB
4) Ước đạc chiều sâu:
Khi đứng ở một độ cao ở một nơi nào đó, thì để muốn biết chiều sâu từ nơi ta đúng đến mặt đất ta chỉ cần tảh một vật nặng rơi tự do (ví dụ: lon nước ngọt, thùng nhôm,…) khi chạm đất sẽ gây tiếng động. Chúng ta chỉ cần tính thời gian rơi tự do là bao nhiêu rồi áp dụng công thức chúng ta sẽ biết được độ cao cần tìm.
Công thức: H = g s2
Với: H : Độ cao (chiều sâu) cần tìm (m)
s : thời gian rơi tự do.
g = 9,8 m/s2 – gia tốc rơi tự do.
5) Cách tạo một góc vuông trên mặt đất:
Có rất nhiều cách để tạo một góc vuông 900 trên mặt đất. Ở đây xin giới thiệu đến các bạn 2 phương pháp cơ bản để tạo góc vuông với những dụng cụ thô sơ (dây, gậy gỗ, phấn…).
Thí dụ muốn vẽ một đường thẳng vuông góc với đoạn AB tại điểm B, ta có 2 phương pháp cơ bản sau:
a) Phương pháp 1 (đường thẳng & tam giác):
- Đầu tiên, ta đóng 1 cọc nhỏ tại điểm B.
- Dùng sợi dây, gập đôi, buộc nút N ở giữa sợi dây để làm dấu.
- Đặt 2 đầu sợi dây ở 2 điểm A & B (khoảng cách AB bất kỳ, tuỳ theo chiều dài sợi dây). Kéo điểm N làm căng sợi dây rồi đóng 1 cọc nhỏ tại điểm N để giữ căng sợi dây.
- Đem đầu B của sợi dây đến điểm C sao cho 3 điểm A, N, C thẳng hàng. Dùng phấn hoặc gậy (nếu đất cát) nối 3 điểm A, B, C lại ta có một tam giác vuông.
- Như vậy, ta đã vẽ được một tam giác vuông ABC có góc vuông tại B.
- Đầu tiên, ta đóng 2 cọc nhỏ tại 2 điểm A & B. Đoạn thẳng AB dài bất kỳ tuỳ theo chiều dài sợi dây và tay vẽ.
- Dùng 1 sợi dây có chiều dài, dài hơn ½ đoạn AB. Ta vẽ 2 đường tròn có 2 tâm là tâm A &tâm B với bàn kính của 2 đường tròn là chiều dài sợi dây. Hai đường tròn giao nhau tại 2 điểm C & D.
- Ta vẽ 1 đường thẳng tại 2 điểm giao nhau của 2 đường tròn. Như vậy, ta đã vẽ được đoạn thẳng CDvuông góc với đoạn thẳng AB.
1) Ước lượng diện tích:
- Để ước lượng một diện tích (một mảnh đất, thửa ruộng, khu vườn…) chúng ta phải tập luyện bằng phương pháp so sánh bằng mắt. So sánh bằng mắt giữa một diện tích thật đã biết trước với diện tích cần so sánh. sau đó, chúng ta sẽ kiểm chứng lại diện tích đó bằng phương pháp đo ước đạc với các công thức thích hợp.
- công thức áp dụng
iện tích hình chữ nhật, hình vuông: (Chiều dài + chiều rộng)* 2 (đơn vị tính m2).
- Cách tập luyện cũng giống phương pháp như trên, nghĩa là chúng ta tập nhìn cho quen một số đông được ấn định (10 hoặc 20 người), rồi tập nhìn số đông được ấn định đó ở nhiều đội hình khác nhau (hàng ngang, hàng dọc, vòng tròn,…) .
- Sau đó so sánh giữa số đông đó với một số đông khác rồi kiểm chứng lại. Tập luyện đến khi nào đạt được tới sai số nhỏ nhất. Khi đó chỉ cần bạn đảo mắt qua là ước lượng được ngay số đông đó (như số đông của buổi họp, 1 cuộc mít tinh, một đại hội…).
- Có rất nhiều phương pháp để ước lượng thời gian. Ở đây xin trình bày một phương pháp thông dụng là ta tập ước lượng thời gian bằng cách đếm số. Bạn chỉ cần đếm to tiếng “301, 302, 303, 304…” và căn cứ trên trên những con số “ 1, 2, 3, 4 … “ ở sau để biết số giây đã trôi qua kể từ khi bắt đầu đếm.
- Trong khi tập, bạn nên kiểm soát trên mặt đồng hồ để tập đọc cho đúng vận tốc trôi qua mỗi giây cho chính xác.
- Có thể tập luyện bằng cách so sánh với những khối lượng đã biết bằng tay. Nghĩa là lúc đầu ta tập cầm những khối lượng trung bình từ 1 đến 5 ký. Lúc tập nên đổi tay qua lại để cho tay quen.
- Ngoài ra chúng ta còn có nhiều phương pháp khác để ước lượng khối lượng (ví dụ như dựa vào thể tích của một vật, khối lượng riêng…).
- Về thời gian dài, ta có thể ước lượng bằng hơi thở. Trung bình một phút ta thở từ 12 đến 14 lần, hãy kiểm chứng bằng đồng hồ cho quen.
- Chúng ta cũng có thể ước lượng thời gian bằng nhịp đập của mạch máu. Tùy theo cơ thể của mỗi người, một phút có thể từ 70 đến 100 nhịp đập. Hãy tự kiểm tra mình trong nhiều tình huống: bình thường, mệt mỏi, làm việc nặng…
- Hoặc chúng ta tập đếm ba trăm lẻ một, ba trăm lẻ hai… (301, 302…) theo một nhịp đều đều.
- Ta tập cầm nhiều lần các vật dụng khác nhau cùng một trọng lượng như: sắt, đường, bông gòn, muối… Dần dần đã quen, ta nâng trọng lượng dần lên. Sau nhiều lần ta sẽ quen và ước lượng gần đúng.
- Phần này phải nói là do quen mắt nhờ lặp đi lặp lại nhiều lần mà thôi. Ta ước lượng chiều dài, chiều rộng và chiều cao sau đó nhân lên.
- Hoặc chúng ta dùng phương pháp so sánh với những diện tích, thể tích, dung tích mà chúng ta đã đo lường kỹ càng. Sau khi ước lượng xong, chúng ta nên kiểm chứng lại. Chỉ sau vài lần là quen.
- Chúng ta tập luyện bằng cách chia ra từng nhóm nhỏ rồi đếm từng người. Sau đó ước lượng xem số đông đó có khoảng bao nhiêu nhóm, rồi nhân lên.
- Các phóng viên là những người ước lượng số đông rất giỏi. Họ chỉ cần đảo mắt qua là ước lượng được ngay số người đang có mặt trong một buổi họp, một buổi mít tinh….
Đo chiều dài
- 1 Metre = 10 decemetres (tấc)
- 1 Decimetre = 10 centimetres (phân)
- 1 Centimetre = 10 millimetres (ly)
- 1 Kilometre = 1.000 mét
- 1 Feet, Foot = 0,3048 mét
- 1 Inch = 2,54 centimét
- 1 Yard = 0,914 mét
- 1 Chain = 20,115 mét
- 1 Furlong = 201 mét (1/8 dặm Anh)
- 1 Mile = 1.603 mét (dặm Anh)
- 144 sq inches = 1 sq foot
- 9 sq feet = 1 sq yard
- 1.210 sq yard = 1 rood (1/4 mẫu Anh)
- 4 Rood = 1 mẫu Anh (Acre)
- 1 Acre (Anh) = 0,4 mẫu (sq hectometre)
- 1 Mẫu (Hecta) = 10.000 m2
- 1.728 cu inches = 1 cu foot
- 27 cu feet = 1 cu yard
- 128 cu feet = 1 cord = 3,63 m3 (đo củi)
- 40 cu feet = 1 ton (tấn Anh)
- 1 Ton (Tấn) = Anh 1.016 kgs
- = Mỹ 907,2 kgs
- = Việt 1.000 kgs
- = Dung tích tàu 2,831 m3
- = Trọng tải tàu 1,12 m3
- 2.150,42 cu inch = 1 standard 4,5 m3 gỗ
- 1 cu foot = gần 4/5 Bushel (đo giạ)
- 1 Bushel = gần bằng 36 lít # 30 kgs
- 60 Minims = 1 Fluid drachm
- 1 Drachm (đồng dram đo chất lỏng) 1,77gr
- 8 Flu. Drachms = 1 Fluid Ounce 28,35gr
- 20 Flu. Ounce = 1 Pint 0.57 lít Mỹ
- 1 Pint = 0.141 lít Anh
- = 0,118 lít Mỹ
- 1 Quart = 1,135 lít Anh (1/4 gallon)
- 1 Gallon = 4,54 lít Anh – 3,78 lít Mỹ
- 1 Barrel = Thùng 150 lít
- 1 Hogshead = Thùng 238 lít
- 1 Sải – Fathom = Sâu 1,82 mét
- 1 Tầm – Cable length = 183m (219m Mỹ)
- 1 Hải lý, dặm = 7 1/2 cable-length
- 1.372,5 mét (1.642,5m Mỹ)
- 5.280,2 feet = 1 Hải lý luật quy định
- 6.080,2 feet = 1 Hải lý thuộc biển
- Đo trắc địa
- 7,93 inches = 1 Link = 0,20 mét/mắt
- 25 Link = 1 Rod # 5 mét sào Anh
- 4 Rod = 1 Chain = 20,115 mét
- 10 sq chains hay 160 sq rods = 1 Acre
- 640 Acres = 1 sq Mile
- 36 sq mile = 1 quận, huyện
- 16 Grams = 1 Ounce 28,35 grams
- 16 Ounces = 1 Pound (Lbs) 54,36 gr
- 14 Pound = 1 Quarier
- 4 Quariers = 1 Cwt
- 20 Cwts = 1 Ton (2.240 Lbs)
- 2.000 Pounds = 1 Short Ton (ngắn)
- 2.240 Pounds = 1 Long Ton (dài)