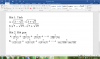
mọi người ơi giúp mình với, mai mình nộp rồi T_T
Bài $1$ $:$
$a)$ Đặt $A=\sqrt {3-\sqrt {5}}-\sqrt {3+\sqrt {5}}$
Khi đó $:$ $A^{2}=\left( \sqrt {3-\sqrt {5}}-\sqrt {3+\sqrt {5}}\right) ^{2}=\left( \sqrt {3-\sqrt {5}}\right) ^{2}-2\sqrt {\left( 3-\sqrt {5}\right) \left( 3+\sqrt {5}\right) }+\left( \sqrt {3+\sqrt {5}}\right) ^{2}$
$\Leftrightarrow A^{2}=3-\sqrt {5}-2\sqrt {9-5}+3+\sqrt {5}=6-2\sqrt {4}=6-2.2=6-4=2$
Ta có $:$ $\sqrt {3-\sqrt {5}} < \sqrt {3+\sqrt {5}}\Leftrightarrow \sqrt {3-\sqrt {5}}-\sqrt {3+\sqrt {5}} < 0\Leftrightarrow A < 0$
Vậy nên $A=\sqrt {3-\sqrt {5}}-\sqrt {3+\sqrt {5}}=-\sqrt {2}$
$b)$ Đặt $B=\sqrt {7-\sqrt {19}}-\sqrt {7+\sqrt {19}}$
Khi đó $:$ $B^{2}=\left( \sqrt {7-\sqrt {19}}-\sqrt {7+\sqrt {19}}\right) ^{2}=\left( \sqrt {7-\sqrt {19}}\right) ^{2}-2\sqrt {\left( 7-\sqrt {19}\right) \left( 7+\sqrt {19}\right) }+\left( \sqrt {7+\sqrt {19}}\right) ^{2}$
$\Leftrightarrow B^{2}=7-\sqrt {19}-2\sqrt {49-19}+7+\sqrt {19}=14-2\sqrt {30}$
Ta có $:$ $\sqrt {7-\sqrt {19}} < \sqrt {7+\sqrt {19}}\Leftrightarrow \sqrt {7-\sqrt {19}}-\sqrt {7+\sqrt {19}} < 0\Leftrightarrow B < 0$
Vậy nên $B=\sqrt {7-\sqrt {19}}-\sqrt {7+\sqrt {19}}=-\sqrt {14-2\sqrt {30}}$
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.