C
cold_noodles97
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
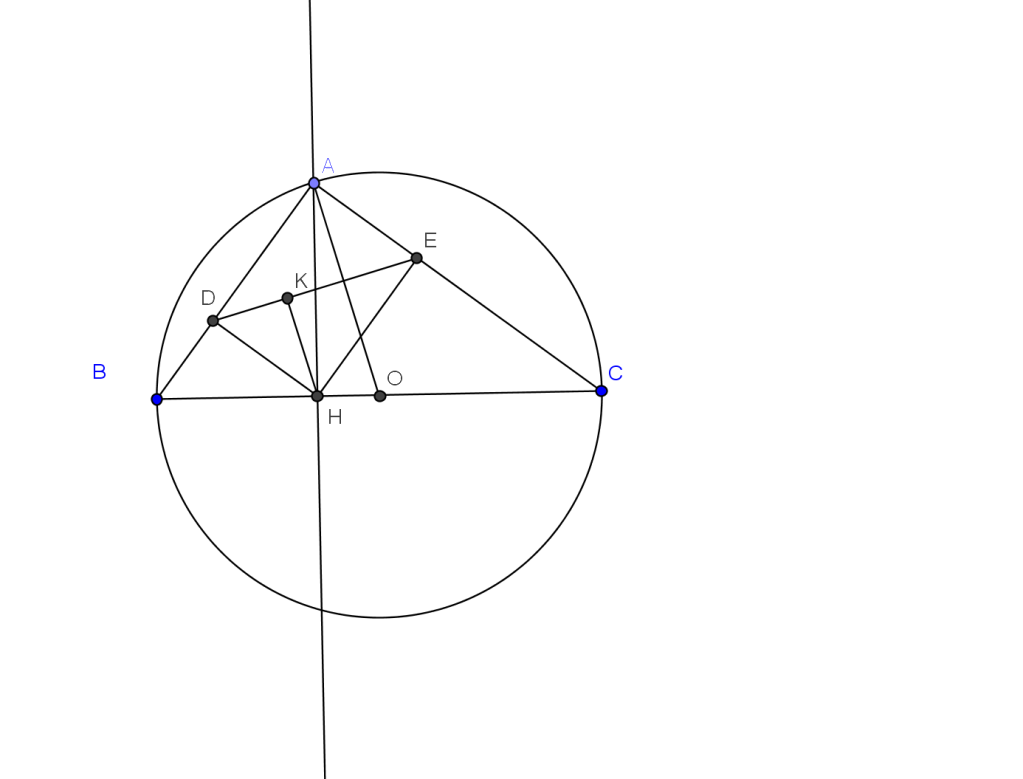
Xét các tam giác vuông ABC có cạnh huyền BC=2a.Gọi AH là đường cao của tam giác,D và E là hình chiếu của H trên AB
a tìm giá trị lớn nhất của DE
b diện tích tứ giác ADHE
a tìm giá trị lớn nhất của DE
b diện tích tứ giác ADHE
Last edited by a moderator: