[Toán 9]Team contest

[shayneward_1997]

Bài 5 lộn đề rùi sửa lại bạn ơi...........................................
Mà sau khi làm bài thi mình phải làm thế nào?(ko chắc làm dc cứ hỏi thôi)
Mà câu cực trị là min hay max

 

[thienlong_cuong]

Bài 5: Bất đẳng thức:
Cho xyzt=1.CMR:
[TEX]\frac{1}{x^2(yz+zt+ty)}+ \frac{1}{y^2(xz+zt+tx)}+ \frac{1}{z^2(yx+xt+ty)}+ \frac{1}{t^2(xy+yz+zx)}\geq \frac{4}{3}[/TEX]

BĐT \Leftrightarrow [TEX]\sum \frac{1}{\frac{x}{y} + \frac{x}{z} + \frac{x}{t} \geq \frac{4}{3}[/TEX]

[TEX]\Leftrightarrow \sum \frac{yzt}{xyz + xzt + xyt} \geq \frac{4}{3}[/TEX]

[TEX]\Leftrightarrow \sum \frac{a}{b +c + d} \geq \frac{4}{3}[/TEX]

Tới đây cộng 4 vào , dùng schwarz là đc

 

[thienlong_cuong]

Bài 3: (số học):n là số nguyên dương thoả mãn 2n+1 và 3n+1 là số chính phương.CMR:
[TEX]n\vdots 40[/TEX]
Bài 5: Bất đẳng thức:
Cho xyzt=1.CMR:
[TEX]\frac{1}{x^2(yz+zt+ty)}+ \frac{1}{y^2(xz+zt+tx)}+ \frac{1}{z^2(yx+xt+ty)}+ \frac{1}{t^2(xy+yz+zx)}\geq \frac{4}{3}[/TEX]

p/s : Hâm mộ BDT ! Giờ hâm mộ sang chia hết tý ! Toàn chon pa`i ko nhỉ !
Dựa vào đồng dư thức
1 số chính phương [TEX]p^2 \equiv{8} (mod 0 ,1 , 4)[/TEX]
[TEX]k^2 \equiv{5} (mod 0 ,1 , 4)[/TEX]

Áp dụng điều này vào bài toán
Chịu khó mò mẫn tý
Giả sử 2n + 1 = p^2 chia hết 5
=> n chia 5 dư 2
Thay vô 3n + 1 = 5k + 2 # k^2 (loại)

Cứ như thế ta sẽ chứng minh đc n chia hết 8 và 5 => đpcm !

Cách hơi dài ! Ai chém cách khác nhé

[TEX]n = (k - p)(k + p)[/TEX] /

 

[thienlong_cuong]

Bài 1: (nghiệm nguyên)Giải phương trình nghiệm nguyên dương(cái này post trên topic số học nhưng chưa có ai giải:
8888..8(n-1 số 8)+8888..8(n-2 số 8)+...+8=8888..8(n số 8)

Bài này nghĩa là sao đây ko thể hiểu nổi ý tưởng là gì !*
Đề có cho ẩn đâu mà tìm Nghiệm !?*******************************************************?????????

 

[thienlong_cuong]

Bài 2 (cực trị):Tìm giá trị lớn nhất của biểu thức:
[TEX]M=14ab+1997bc+2011ac[/TEX]
biết [TEX]a+b+c=1[/TEX](ngon xơi nhất )

Chán quá ! Sao mãi chưa ai lên hầy !
Thôi giết thời gian chém leng cheng bài này
Ai thích cân bằng hệ số thì cân bằng nhé , sư đệ đổi biến thôi ! @-)

[TEX]a + b + c = 1 \Rightarrow c = 1 - a - b[/TEX]

[TEX]14ab + c(1997b + 2011a) = 14ab + (1 - a - b)(1997b + 2011a)[/TEX]

Ùi ! Giờ áp dụng CT tổng quát giải tìm GTNN và Lớn Nhất gì đó của PT bậc 2 2 ẩn !@-)

Đây là cách có lẽ cùn nhất có thể cùn nhỉ !? /

 

[minhtuyb]

[TEX]M=14ab+1997bc+2011ac[/TEX]
biết [TEX]a+b+c=1[/TEX](ngon xơi nhất )

Có:
[TEX]M=14ab+14ac+1997bc+1997ac[/TEX]
[TEX]=14a(b+c)+1997c(a+b)[/TEX]
-Áp dụng bất đẳng thức [TEX]xy\leq \frac{(x+y)^2}{4}[/TEX],ta có:
+)[TEX]a(b+c)\leq \frac{(a+b+c)^2}{4}=\frac{1}{4}[/TEX]
+)[TEX]c(a+b)\leq \frac{(a+b+c)^2}{4}=\frac{1}{4}[/TEX]
Suy ra: [TEX]M\leq 14.\frac{1}{4}+1997.\frac{1}{4}=\frac{2011}{4}[/TEX]
-Dâu bằng xảy ra khi:
[TEX]\left\{\begin{matrix}a=b+c\\c=a+b\\a+b+c=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}a=c=\frac{1}{2}\\ b=0\end{matrix}\right.[/TEX]
Vậy [TEX]MaxM=\frac{2011}{4}[/TEX] khi [TEX]a=c=\frac{1}{2};b=0[/TEX]
Dễ thế này mà không ai ăn nhanh cả, may thật )

 

[son9701]

Bài 1: (nghiệm nguyên)Giải phương trình nghiệm nguyên dương(cái này post trên topic số học nhưng chưa có ai giải:
8888..8(n-1 số 8)+8888..8(n-2 số 8)+...+8=8888..8(n số 8)

Bài này nghĩa là sao đây ko thể hiểu nổi ý tưởng là gì !*
Đề có cho ẩn đâu mà tìm Nghiệm !?*******************************************************?????????

Tìm n là số nguyên dương lớn hơn 2 để:
[TEX]\bar{88.88}+\bar{88..8}+...+88+8=\bar{888..8}[/TEX]

K đánh đc cái ngoặc ở dưới nên chú thích ở đây vậy:
Ở vế trái bắt đầu là số hạng gồm n-1 số 8,sau là só hạng gồm n-2 số 8;...;đến 1 số 8.Vế phải là n số 8.
Dịch ra thế này khó hiểu,văn mình ngu,thôi,ai chỉ hộ viết cái ngoặc ở dưới thế nào vs

 

[zorrono1]

Thiết nghĩ chủ topic nên gom tất cả các nhóm lại, rồi lập 1 bảng thống kê các nhóm và thành viên lại đàng hoàng. Sau đó tạo topic cho mỗi tuần mỗi đấu, như vậy hay hơn chứ nhỉ.

Đây là ý kiến riêng của mình thôi, có gì không đúng thì bỏ quá nhé

 

[mimibili]

Bài 3: (số học):n là số nguyên dương thoả mãn 2n+1 và 3n+1 là số chính phương.CMR:
[TEX]n\vdots 40[/TEX]

Cách khác được ko hềy?
do 2n+ 1 là số cp lẻ => 2n +1 chia 8 dư 1
=> 2n chia hết 8=> n chia hết 4 ( n chẵn)
do n chẵn => 3n +1 lẻ => 3n + 1 chia 8 dư 1=> 3n chia hết 8 mak (3,8)=1
=> n chia hết 8 (1)
xét các TH số cp chia 5 dư 0,1,4 ( như Thienlong_cuong)

 

[minhtuyb]

Bài 8: (dãy số).CMR dãy:
[TEX]u_{n}=3n^2+3n+7;n=1;2;...[/TEX]
k là lập phương 1 số tự nhiên

-Giả sử [TEX]u{n}[/TEX] là lập phương của một số tự nhiên, đặt:
[TEX]3n^2+3n+7=k^3(k\in N*)[/TEX]
[TEX]\Leftrightarrow 3(n^2+n+2)=k^3-1(1)[/TEX]
-Vì [TEX]VT(1)\vdots 3\Rightarrow VP(1)=k^3-1\vdots 3\Rightarrow k^3\equiv 1(mod 3)\Rightarrow k\equiv 1(mod3)[/TEX]. Đặt: [TEX]k=3k_1+1(k \in N*)[/TEX], thay vào [TEX]VP(1)[/TEX] ta có:
[TEX]VP(1)=(3k_1+1)^3-1=27k_1^3+27k_1^2+9k_1 \vdots 9[/TEX]
[TEX]\Rightarrow VT(1)=3(n^2+n+2)\vdots 9\Rightarrow n^2+n+2\vdots 3[/TEX]
-Tuy nhiên, [TEX]n^2+n+2\not\vdots 3[/TEX] vì:
+)Với [TEX]n=3n_1\Rightarrow n^2+n+2=9n_1^2+3n_1+2\not\vdots 3[/TEX]
+)Với [TEX]n=3n_1+1\Rightarrow n^2+n+2=9n_1^2+9n_1+4\not\vdots 3[/TEX]
+)Với [TEX]n=3n_1+2\Rightarrow n^2+n+2=9n_1^2+15n_1+8\not\vdots 3[/TEX]
[TEX]\Rightarrow [/TEX]Điều giả sử sai [TEX]\Rightarrow u_{n}[/TEX]không là lập phương 1 số tự nhiên<DPCM>
Thanks mình nha chủ pic

 

[minhtuyb]

Bài 7: (Tổ hợp):Có 6 chú chim đang ở trên 1 sân bay có kích thức 3x4 (giả thiết thôi).CMR:Luôn có 2 chú chim có khoảng cách nhỏ hơn hoặc bằng [TEX]\sqrt{5}[/TEX]

-Diện tích sân bay là : [tex]3.4=12[/tex]
-Chia sân bay thành 4 ô vuông có [TEX]S=\frac{5}{2}\Rightarrow[/TEX] có đường chéo là [TEX]\sqrt{5}[/TEX] và 1 ô vuông có [TEX]S=2\Rightarrow[/TEX] có đường chéo là [TEX]2<\sqrt{5}[/TEX] (Tổng cộng có 5 ô vuông)
-Theo Nguyên lí Đi-ríc-lê, có ít nhất 2 con nhím ở trong cùng một ô vuông. Không mất tính tổng quát, giả sử 2 con nhím đó là [TEX]A[/TEX] và [TEX]B[/TEX]. Vì 2 con nhím nằm trong ô vuông có đường chéo [TEX]\sqrt{5}[/TEX] hoặc [TEX]2<\sqrt{5}[/TEX] nên ta luôn có:
[TEX]AB\leq \sqrt{5}[/TEX]
[TEX]\Rightarrow[/TEX] Khoảng cách giữa 2 con nhím nhỏ hơn hoặc bằng [TEX]\sqrt{5}[/TEX] [TEX]\Rightarrow[/TEX] Luôn tồn tại 2 chú chim có khoảng cách nhỏ hơn hoặc bằng [TEX]\sqrt{5}[/TEX] trên sân bay <DPCM>

 

[minhtuyb]

Trước hết tớ xin lỗi các bạn (nhiệt tình ghê cơ)về sự chậm chễ trog việc post bài.
Bài 1: (nghiệm nguyên)Giải phương trình nghiệm nguyên dương(cái này post trên topic số học nhưng chưa có ai giải:
8888..8(n-1 số 8)+8888..8(n-2 số 8)+...+8=8888..8(n số 8)

Hình như bài này vô nghiệm nguyên dương@-), mình giải thử nha:
-Nhận xét: 999...99(k số 9)=[TEX]10^k-1(k\in N*)[/TEX]. Áp dụng công thức trên, ta có:
8888..8(n-1 số 8)+8888..8(n-2 số 8)+...+8=8888..8(n số 8)
[TEX]\Leftrightarrow[/TEX] 999...9(n-1 số 9)+999..99(n-2 số 9)+...+9=999.99(n số 9)
[TEX]\Leftrightarrow 10^{n-1}-1+10^{n-2}-1+...+10^1-1=10^n-1[/TEX]
[TEX]\Leftrightarrow (10^{n-1}+10^{n-2}+...+10^1+1)-(1+1+1+...+1)(n-1\, so\, 1)=10^n(1)[/TEX]
-Đặt [TEX]S=10^{n-1}+10^{n-2}+...+10^1+1[/TEX] thì:
[TEX](1)\Leftrightarrow S-(n-1)=10^n[/TEX]
[TEX]\Leftrightarrow S=10^n+n-1[/TEX]
[TEX]\Leftrightarrow 9S=9.10^n+9n-9(2)[/TEX]
-Mặt khác, ta có:
[TEX]S=10^{n-1}+10^{n-2}+...+10^1+1[/TEX]
[TEX]\Rightarrow 10S=10^n+10^{n-1}+...+10^1[/TEX]
[TEX]\Rightarrow 9S=10S-S=10^n-1[/TEX]
-Thay vào (2) ta có:
[TEX]10^n-1=9.10^n+9n-9[/TEX]
[TEX]\Leftrightarrow8.10^n=-9n+8(2')[/TEX]
Lại có: Vì [TEX]n\in N*[/TEX] nên [TEX]VT(2')>0;VP(2')<0\Rightarrow[/TEX] Pt (2') vô nghiệm nguyên dương [TEX]\Rightarrow[/TEX] Không tồn tại số n dương thỏa mãn đề bài
Chả bít đúng không zz :-SS

 

[minhtuyb]

Bài 6: (Hình học):Cho tam giác ABC cân tại A có [TEX]\hat{BAC}=36^o[/TEX].CMR:[TEX]\frac{BA}{BC}[/TEX]là 1 số vô tỉ(dễ)

Bài này dễ......................................xương vãi @-):

*Không mất tính tổng quát, giả sử [TEX]BC=1[/TEX](đvđd). Giờ ta phải chứng minh AB là số vô tỉ. Thật vậy, ta có:
-Dễ dàng tính được [TEX]\widehat{ABC}=\widehat{ACB}=72^o[/TEX]. Kẻ p/giác [TEX]AD[/TEX] của [TEX]\widehat{ABC}\Rightarrow[/TEX]
+)[TEX]\widehat{ABD}=\widehat{BAC}=\widehat{CBD}=36^o\Rightarrow \Delta ABD[/TEX] cân tại [TEX]D\Rightarrow AD=BD(1)[/TEX]
+)[TEX]\widehat{BDC}=72^o[/TEX](Góc ngoài của tam giác) [TEX]\Rightarrow \widehat{BDC}=\widehat{ACB}\Rightarrow \Delta BDC[/TEX] cân tại [TEX]B\Rightarrow BC=BD(2)[/TEX]
-Từ (1) và (2) [TEX]\Rightarrow AD=BD=BC=1[/TEX]
-Kẻ p/giác [TEX]DE[/TEX] của [TEX]\widehat{BDC}\Rightarrow [/TEX]
+)[TEX]\widehat{BDE}=\widehat{EBD}=36^o\Rightarrow \Delta BDE[/TEX] cân tại [TEX]E\Rightarrow EB=ED(3)[/TEX]
+)[TEX]ED//AB[/TEX] (so le trong).
+)[TEX]\widehat{DEC}=72^o[/TEX](Góc ngoài của tam giác)[TEX]\Rightarrow \widehat{DEC}=\widehat{DCE}\Rightarrow \Delta DEC [/TEX] cân tại [TEX]D\Rightarrow DE=DC(4)[/TEX]
-Từ (3) và (4)[TEX]\Rightarrow EB=ED=CD[/TEX]
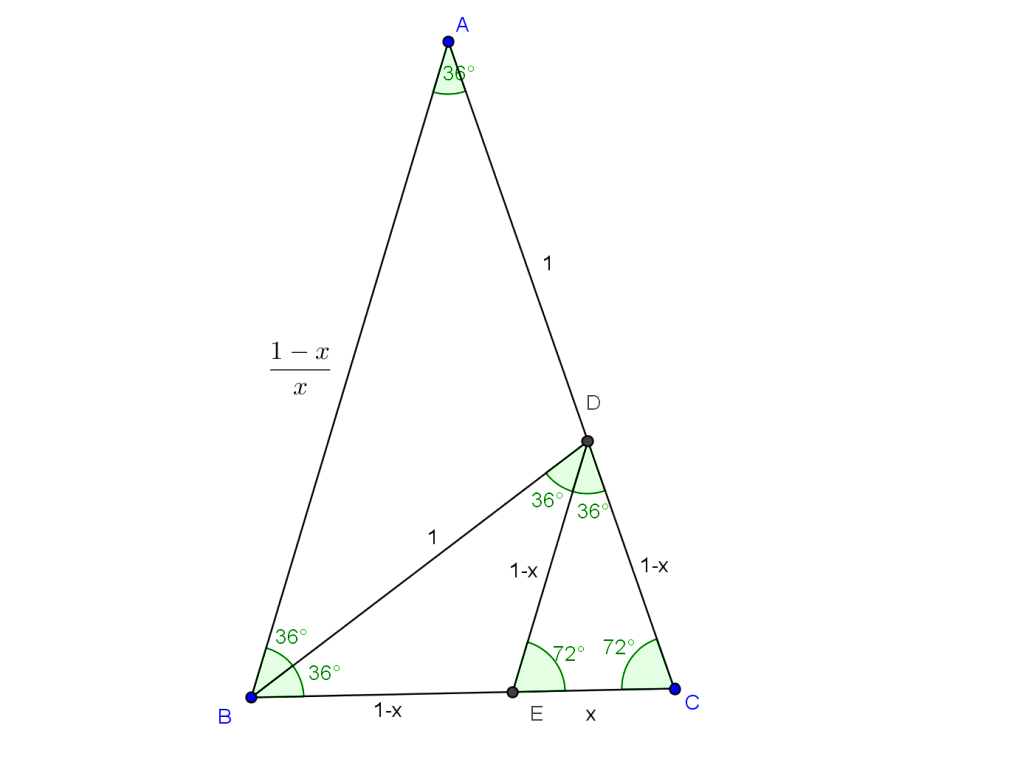
-Đặt [TEX]EC=x(0<x<1)\Rightarrow EB=ED=CD=1-x\Rightarrow AC=AD+CD=1+1-x=2-x[/TEX]@-)
-Áp dụng hệ quả Talet vào [TEX]\Delta ABC (ED//AB)\Rightarrow \frac{AB}{BC}=\frac{DE}{EC}\Rightarrow \frac{AB}{1}=\frac{1-x}{x}\Rightarrow AB=\frac{1-x}{x}[/TEX]@-)@-)
-Vì [TEX]AB=AC[/TEX], kết hợp với @-) và @-)@-) ta có phương trình:
[TEX]2-x=\frac{1-x}{x}[/TEX]
Hix đánh latex ngại quá, các bạn giải pt bậc hai trên ra tính đc [TEX]x=\frac{3\pm \sqrt{5}}{2}[/TEX]. Tuy nhiên [TEX]x<1\Rightarrow x=\frac{3-\sqrt{5}}{2}[/TEX]
-Suy ra [TEX]AB=AC=AD+CD=1+(1-\frac{3-\sqrt{5}}{2})=\frac{1+\sqrt{5}}{2}[/TEX] là số vô tỉ [TEX]\Rightarrow \frac{BA}{BC}= \frac{1+\sqrt{5}}{2}[/TEX] là số vô tỉ <DPCM>
Trong lúc đánh latex mỏi tay, bài giải có gì sơ suất xin đc lượng thứ, tui xin chân thành cảm ơn =))=))

 

[harrypham]

Xin lỗi, cho em xin một chân đăng kí, tuy không giải được nhiều nhưng hứng thú với mấy bài số bên topic này. Dạo này thấy ít Lý thuyết số quá nên mò sang đây.

 

[son9701]

Vì vẫn còn 1 số bài tập chưa được giải và tớ cũng k có điều kiện online nhiều nên tớ sẽ lùi hạn post bài lên thứ 2 tuần sau

 

[daovuquang]

Bài 4: (Biến đổi đồng nhất):Cho a;b;c đôi một khác nhau.CMR:
[TEX]P=a^4(b-c)+b^4(c-a)+c^4(a-b) \neq 0[/TEX]

Giờ chắc vẫn giải được nhỉ.
Phân tích đa thức P thành nhân tử, ta được:
[TEX]P=(a-b)(b-c)(a-c)(a^2+b^2+c^2+ab+bc+ca)[/TEX]
Theo đề bài, a; b; c đôi một khác nhau vậy (a-b),(b-c),(c-a) khác 0.
Mặt khác [TEX]a^2+b^2+c^2+ab+bc+ca[/TEX] phải khác 0 (vì nếu nó bằng 0 sẽ dẫn đến a=b=c=0\Rightarrow loại)
Kết hợp những điều trên, ta có đpcm.

 

[minhtuyb]

Post đề nào sơn ơi, đề giải gần hết òi mà hum nay thứ 3 rùi đó [-(
P/s: Added Team gồm những ai nhỉ, gừi zô tin nhắn cá nhân cho mình nha

 

[son9701]

Đề thi tuần thứ 2:
1/Tìm tất cả các số nguyên tố có dạng:
[TEX]P=n^n+1[/TEX]
với n là 1 số nguyên dương và P có ít hơn 20 chữ số
2/CMR:
[TEX]\sqrt[3]{1+c^3}\sqrt[3]{1+b^3}+\sqrt[3]{1+c^3}\geq \sqrt[3]{27+(a+b+c)^3}[/TEX]
với a;b;c k âm
3/CMR: Trong các tam giác vuông có chu vi bằng nhau,tam giác vuông cân là tam giác có diện tích lớn nhất
4/CMR:Trong các tam giác có chu vi bằng nhau,tam giác đều là tam giác có diện tích lớn nhất
5/Tìm max của:
[TEX]A=\frac{1}{(a+2b+c)^2}+\frac{1}{(a+b+2c)^2}+\frac{1}{(2a+b+c)^2}[/TEX]
với [TEX]\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\leq \frac{1}{2011}[/TEX] và a;b;c >0
6/Trên 1 mặt phẳng vẽ 1 đa giác lồi n cạnh sao cho cứ 3 đoạn thẳng bất kì nối từ 3 đỉnh của đa giác ta luôn nhận đc 1 tam giác vuông cân .Cmr: đa giác lồi đó k thể có n(n-1)/2 đoạn có số đo là số nguyên.
7/Tìm số hữu tỉ x để [TEX]x^2+8x[/TEX]là 1 số chính phương
8/Cho tam giác ABC nhọn.Gọi R là bán kính đtròn ngoại tiếp.r là bán kính đtròn nội tiếp
8.1/CMR:R>2r(10 điểm)
8.2:Giải bất phg trình: R>3r(15 điểm)
9/Cho 100 số tự nhiên :1;2;...;100.Gọi A là số thu đc từ cách viết 100 số tự nhiên đó thành 1 dãy.B là số thu đc từ cách đặt dấu cộng vào giữa các số của A(tuỳ ý)
CMR: cả A và B đều không chia hết cho 2010

Cố lên.Chai dzô

 

[harrypham]

7/Tìm số hữu tỉ x để [TEX]x^2+8x[/TEX]là 1 số chính phương

harrypham xin giải bài 7

Đặt [TEX]x^2+8x=y^2 \ (y \in \mathbb{N})[/TEX].

Đầu tiên, ta cần chứng minh [TEX]x[/TEX] nguyên. Thật vậy giả sử x không là số nguyên, đặt [TEX]x= \frac{m}{n}, \ (m,n)=1, \ n \neq 0[/TEX].
Ta có [TEX]\left( \frac{m}{n} \right)^2=8. \frac{m}{n}=y^2 \Leftrightarrow m^2+8mn=y^2n^2[/TEX]
[TEX]\Rightarrow m^2 \ \vdots n[/TEX], trái với giả thiết [TEX](m,n)=1[/TEX].

Ta có [TEX]x^2+8x=y^2 \Leftrightarrow 4x^2+32x=4y^2 \Leftrightarrow (2x+8)^2-(2y)^2=64[/TEX]
[TEX]\Leftrightarrow (2x+8+2y)(2x+8-2y)=64[/TEX].

Đến đây ta xét, y>0 hay y=0 để giải tiếp.

 

[minhtuyb]

9/Cho 100 số tự nhiên :1;2;...;100.Gọi A là số thu đc từ cách viết 100 số tự nhiên đó thành 1 dãy.B là số thu đc từ cách đặt dấu cộng vào giữa các chữ số của A(tuỳ ý)
CMR: cả A và B đều không chia hết cho 2010

Tổng các chữ số từ [TEX]1\rightarrow 9:1+2+...+9=45 \vdots 3[/TEX]
Tổng các chữ số từ [TEX]10\rightarrow 19:(1+2+...+9)+1+1+...+1(9\ so \ 1)=45+9 \vdots 3[/TEX]
Tổng các chữ số từ [TEX]20\rightarrow 29:(1+2+...+9)+2+2+...+2(9\ so \ 2)=45+9.2 \vdots 3[/TEX]
...
Tổng các chữ số từ [TEX]90\rightarrow 99:(1+2+...+9)+9+9+...+9(9\ so \ 9)=45+9.9 \vdots 3[/TEX]
Tổng các chữ số của số 100:[TEX]1+0+0=1 \not\vdots 3[/TEX]
[TEX]\Rightarrow[/TEX]Tổng các chữ số của các số từ 1 đến 100 [TEX]\not\vdots 3\Rightarrow A,B\not\vdots 3\Rightarrow A,B \not\vdots 3.670=2010<DPCM>[/TEX]