N
netnewqb
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Anh em cùng nhau thảo luận giúp
Câu 1:
So sánh 2 số A, B
[tex] A=\frac{(2^4+\frac{1}{4})(4^4+\frac{1}{4})(6^4+\frac{1}{4})...(32^4+\frac{1}{4})}{(1^4+\frac{1}{4})(3^4+\frac{1}{4})(5^4+\frac{1}{4})...(31^4+\frac{1}{4})}[/tex]
B = 2012
Câu 2:
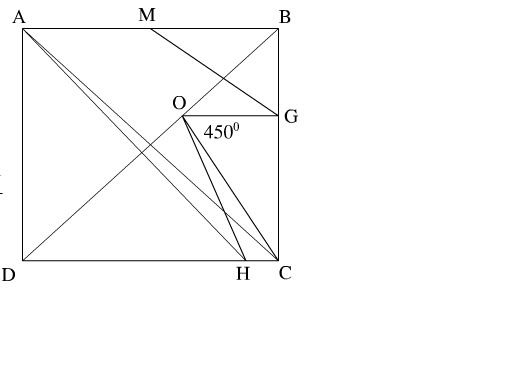
Cho hình vuông ABCD, O là giao điểm hai đường chéo. Lấy G thuộc cạnh BC, H thuộc CD sao cho góc GOH = 45 độ. Gọi M là trung điểm của AB.
Chứng minh:
a)Tam giác HOD đồng dạng với tam giác OGB (làm được rồi)
b) MG //AH (Chưa làm được)
Câu 3
Cho n số [tex] a_1; a_2;...a_n[/tex] mỗi số trong chúng bằng 1 hoặc -1 và [tex] a_1a_2 + a_2a_3 +... + a_na_1 = 0[/tex]. Hỏi n có thể bằng 2010 được không? Vì sao?
Câu 1:
So sánh 2 số A, B
[tex] A=\frac{(2^4+\frac{1}{4})(4^4+\frac{1}{4})(6^4+\frac{1}{4})...(32^4+\frac{1}{4})}{(1^4+\frac{1}{4})(3^4+\frac{1}{4})(5^4+\frac{1}{4})...(31^4+\frac{1}{4})}[/tex]
B = 2012
Câu 2:
Cho hình vuông ABCD, O là giao điểm hai đường chéo. Lấy G thuộc cạnh BC, H thuộc CD sao cho góc GOH = 45 độ. Gọi M là trung điểm của AB.
Chứng minh:
a)Tam giác HOD đồng dạng với tam giác OGB (làm được rồi)
b) MG //AH (Chưa làm được)
Câu 3
Cho n số [tex] a_1; a_2;...a_n[/tex] mỗi số trong chúng bằng 1 hoặc -1 và [tex] a_1a_2 + a_2a_3 +... + a_na_1 = 0[/tex]. Hỏi n có thể bằng 2010 được không? Vì sao?
Last edited by a moderator: