G
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I
iloveckp_01
G
girl_thuy_kute
Mình bít vài bài toán hình 7 nào hay cả! để mình đăng cho nhé!
Ukm!!.............
Ukm!!.............
Last edited by a moderator:
D
dtfbkq
Giải giúp mình bài này với:
Trên bảng có 12 dấu cộng và 9 dấu trừ, 1 người chơi nỗi lần xóa 2 dấu bất kỳ. Nếu xóa 2 dấu giống nhau thì viết thêm lên bảng 1 dấu cộng. Nếu xóa 2 dấu khác nhau thì viết lên bảng 1 dấu trừ. Hỏi sau 1 số lần đoán thì trên bảng còn lại dấu gì? Tại sao?
Trên bảng có 12 dấu cộng và 9 dấu trừ, 1 người chơi nỗi lần xóa 2 dấu bất kỳ. Nếu xóa 2 dấu giống nhau thì viết thêm lên bảng 1 dấu cộng. Nếu xóa 2 dấu khác nhau thì viết lên bảng 1 dấu trừ. Hỏi sau 1 số lần đoán thì trên bảng còn lại dấu gì? Tại sao?
L
lengocminhtam
Trên cạnh BC của tam giác ABC lấy D,E sao cho BD=CE. Qua d và E vẽ các đường thẳng song song với AB cắt AC tai F,G. CMR : DF+EG=AB
__________________________________
_______________________________________________
Thứ tớ cần không phải là thể xác......
..... mà là trái tim cậu cơ
:khi (12)::khi (86)::khi (12):
__________________________________
_______________________________________________
Thứ tớ cần không phải là thể xác......
..... mà là trái tim cậu cơ
:khi (12)::khi (86)::khi (12):
T
trmyidol
Mình bít vài bài toán hình 7 nào hay cả! để mình đăng cho nhé!
Ukm!!.............[/QUOTE
Đăng đi bạn
N
nguoibantriky_thv@yahoo.com
đóng góp cho mọi nguoi bài này nè.ai làm ra khen tài:cho tam giác ABC vuông cân tại A.M là trung điểm của BC.Trên cạnh MC lấy điểm D bất kì.Vẽ BH,CK vuông góc voi AD.Chung minh tam giác MHK vuông cân.
N
nguoibantriky_thv@yahoo.com
là 180 độ.bạn oi.quá dễ.cái này là định lí rồi màcho tam giac ABC
tong 3 goc trong tam giac ABC la bn
L
lonely5x
L
lengocminhtam
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy E sao cho BD = CE. Vẽ DH và EK cùng vuong góc với đường thẳng BC. CM:
a) HB = CK
b) Góc AHB = Góc AKC
c) HK // DE
d) Tam giác AHE = tam giác ADK
e) Gọi I là giao điểm của DK và EH. CM AI vuông góc với DE
___________________________________
________________________________
_____________________________
:khi (79):
a) HB = CK
b) Góc AHB = Góc AKC
c) HK // DE
d) Tam giác AHE = tam giác ADK
e) Gọi I là giao điểm của DK và EH. CM AI vuông góc với DE
___________________________________
________________________________
_____________________________
:khi (79):
I
iceghost
Trên cạnh BC của tam giác ABC lấy D,E sao cho BD=CE. Qua d và E vẽ các đường thẳng song song với AB cắt AC tai F,G. CMR : DF+EG=AB
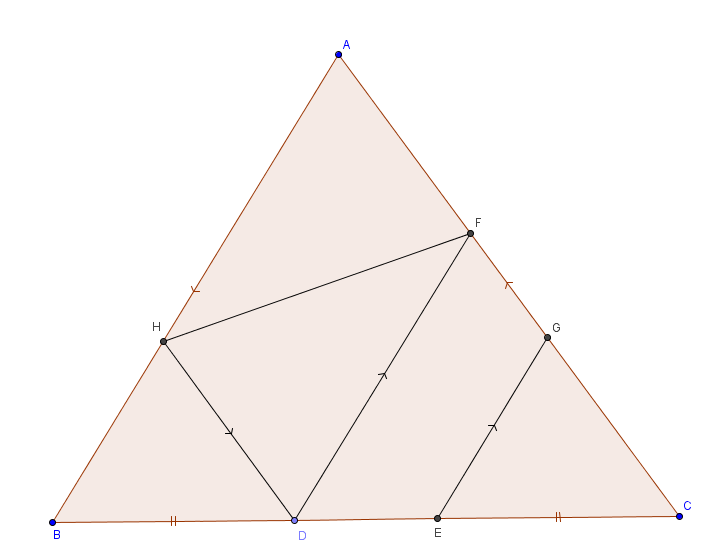
Qua D vẽ DH // AC ( H [TEX]\in[/TEX] AB )
Xét $\triangle$ AHF và $\triangle$ DFH có :
$\widehat{AFH} = \widehat{DHF}$ (So le trong)
HF là cạnh chung
$\widehat{AHF} = \widehat{DFH}$ (So le trong)
Vậy $\triangle$ AHF = $\triangle$ DFH (g.c.g)
Xét $\triangle$ HDB và $\triangle$ GCE có :
$\widehat{HDB} = \widehat{GCE}$ (Đồng vị)
BD = EC (gt)
$\widehat{HBD} = \widehat{GEC}$ (Đồng vị)
Vậy $\triangle$ HDB = $\triangle$ GCE (g.c.g)
Ta có : AH + HB = AB
Mà AH = DF ($\triangle$ AHF = $\triangle$ DFH)
HB = EG ($\triangle$ HDB = $\triangle$ GCE)
\Rightarrow DF + EG = AB
D
duyvt6663
đóng góp cho mọi nguoi bài này nè.ai làm ra khen tài:cho tam giác ABC vuông cân tại A.M là trung điểm của BC.Trên cạnh MC lấy điểm D bất kì.Vẽ BH,CK vuông góc voi AD.Chung minh tam giác MHK vuông cân.
bài này cũng dễ so với mình
này nhé:
xét $\Delta ABC$ vuông cân tại A có: $\widehat{ACB}=45^o_{(1)}$ và $\hat{A}=90^o$
vì $\Delta ABC$ cân tại A nên AM đồng thời là tia phân giác của $\hat{A}$
\Rightarrow $\widehat{MAC}=\widehat{MAB}=45^o_{(2)}$
Từ (1) và (2) suy ra : $\widehat{ACB}=\widehat{MAC}$
\Rightarrow $\Delta{MAC}$ cân tại M
\Rightarrow MA=MC
xét $\Delta{AKC}$ vuông tại K có:
$\widehat{KAC}+\widehat{ACK}=90^o_{(3)}$(theo định lí về các góc trong tam giác vuông)
Ta lại có: $\hat{A}=90^o$(cmt)
\Leftrightarrow $\widehat{KAC}+\widehat{BAK}=90^o_{(4)}$
Từ(3) và (4) suy ra: $\widehat{ACK}=\widehat{BAK}$
Xét $\Delta{BAH}$ vuông tại H và $\Delta{ACK}$ vuông tại K có:
cạnh huyền: AB=AC( do $\Delta{ABC}$ cân tại A)
góc nhọn:$\widehat{BAK}=\widehat{ACK}$(cmt)
do đó $\Delta{BAH}=\Delta{ACK}$(cạnh huyền-góc nhọn)
\Rightarrow AH=CK(cặp cạnh tương ứng)
vì $\widehat{BAH}=\widehat{ACK}$(cmt)
nên $\widehat{BAM}+\widehat{MAH}$=$\widehat{ACM}+\hat{MCK}$
mà $\widehat{BAM}=\widehat{ACM}$(cmt)
\Rightarrow $\widehat{MAH}=\widehat{MCK}$
xét $\Delta{MAH}$ và $\Delta{MCK}$ có:
MA=MC(cmt)
$\widehat{MAH}=\widehat{MCK}$(cmt)
AH=CK(cmt)
do đó $\Delta{MAH}=\Delta{MCK}$(c.g.c)
\Rightarrow MH=MK(cặp cạnh tương ứng) và $\widehat{AMH}=\widehat{CMK}$(cặp góc tương ứng)
vì $\Delta{ABC}$ cân tại A nên AM đồng thời là đường cao ứng với BC
\Rightarrow $AM\perp BC$
\Rightarrow $\widehat{AMC}=90^o$
\Rightarrow $\widehat{AMH}+\widehat{HMC}=90^o$
mà $\widehat{AMH}=\widehat{CMK}$(cmt)
\Rightarrow $\widehat{CMK}+\widehat{HMC}=90^o$
\Rightarrow $\widehat{HMK}=90^o$
xét $\Delta{HMK}$ có:
MH=MK(cmt)
$\widehat{HMK}=90^o$(cmt)
vậy $\Delta{HMK}$ vuông cân tại M
N
nguyenbaongocnx1
Cho tam giác ABC có góc B lớn hơn góc C . AE là tia phân giác góc ngoài đỉnh A,cắt BC tại E . Chứng minh: góc AEB bằng một nửa của góc ABC trừ đi góc ACB
N
nhatheo797
180......................................................................................cho tam giac abc
tong 3 goc trong tam giac abc la bn

