[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài này em thấy nhiều người cho ra nhiều đáp án nên vẫn không biết đáp án nào mới đúng, mong mn giúp ạ!
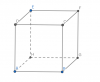
Đề: Tô màu 8 đỉnh của một khối lập phương bằng 4 màu khác nhau. Hỏi xác suất để không có 2 đỉnh thuộc 1 cạnh của khối lập phương cùng màu?
Đề: Tô màu 8 đỉnh của một khối lập phương bằng 4 màu khác nhau. Hỏi xác suất để không có 2 đỉnh thuộc 1 cạnh của khối lập phương cùng màu?