Toán 12 Tính V khối trụ

[minhloveftu]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

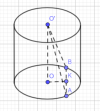
Câu 46: Cho hình trụ có hai đáy ra hai hình tròn [imath](O)[/imath] và [imath]\left(O^{\prime}\right)[/imath], bán kính đáy [imath]r=5[/imath]. Biêt [imath]A B[/imath] là một dây cung của đường tròn [imath](O)[/imath] sao cho tam giác [imath]O^{\prime} A B[/imath] là tam giác đều và mặt phẳng [imath]\left(O^{\prime} A B\right)[/imath] tạo với mặt phẳng chứa hình tròn [imath](O)[/imath] một góc [imath]60^{\circ}[/imath]. Thể tích của khối trụ đã cho bằng
A. [imath]\dfrac{375 \sqrt{7} \pi}{7}[/imath].
B. [imath]25 \sqrt{5} \pi[/imath].
C. [imath]75 \sqrt{5} \pi[/imath].
D. [imath]\dfrac{125 \sqrt{7} \pi}{7}[/imath].


giúp em câu này với ạ

 

[Alice_www]

View attachment 210776
giúp em câu này với ạ

landghost
Gọi K là trung điểm của AB
Gọi AB=x
[imath]\Rightarrow OK=\sqrt{r^2-\dfrac{AB^2}4}=\sqrt{25-\dfrac{x^2}4}[/imath]
[imath]O'AB[/imath] là tam giác đều [imath]\Rightarrow O'K=\dfrac{x\sqrt3}2[/imath]
góc giữa (O'AB) và mặt phẳng chứa hình tròn là [imath]\widehat{O'KO}=60^\circ[/imath]
[imath]\cos \widehat{O'KO}=\dfrac{OK}{O'K}=\dfrac{1}2[/imath]
[imath]\Rightarrow 2\sqrt{25-\dfrac{x^2}4}=\dfrac{x\sqrt3}2\Rightarrow x=\dfrac{20\sqrt7}7[/imath]
[imath]\Rightarrow OO'=\dfrac{15\sqrt7}7[/imath]
[imath]\Rightarrow V=\pi r^2OO'=\dfrac{375\sqrt7\pi}7[/imath]

Có gì khúc mắc em hỏi lại nhé
Ngoài ra em xem thêm tại Mặt cầu, mặt trụ, mặt nón