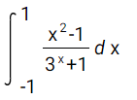Bài toán tổng quát:
Cho hàm số [imath]f(u)[/imath] liên tục trên [imath]\mathbb{R}[/imath] với [imath]f(u)[/imath] là hàm chẵn, tính tích phân:
[imath]\displaystyle \int ^{\alpha} _{-\alpha} \frac{f(u)}{a^u+1} du[/imath]
Lời giải
[imath]\displaystyle \int ^{\alpha} _{-\alpha} \frac{f(u)}{a^u+1} du\\= \displaystyle \int ^{0} _{-\alpha} \frac{f(u)}{a^u+1} du + \displaystyle \int ^{\alpha} _{0} \frac{f(u)}{a^u+1} du \\ u=-t\Rightarrow du=-dt\\ \displaystyle \int ^{\alpha} _{0} \frac{f(-t)}{a^{-t}+1} dt + \displaystyle \int ^{\alpha} _{0} \frac{f(u)}{a^u+1} du\\= \displaystyle \int ^{\alpha} _{0} a^t.\frac{f(t)}{a^{t}+1} dt + \displaystyle \int ^{\alpha} _{0} \frac{f(u)}{a^u+1} du\\=\displaystyle \int ^{\alpha} _{0} a^u.\frac{f(u)}{a^{u}+1} du + \displaystyle \int ^{\alpha} _{0} \frac{f(u)}{a^u+1} du\\= \displaystyle \int ^{\alpha} _{0}(a^u+1) \frac{f(u)}{a^u+1} du \\= \displaystyle \int ^{\alpha} _{0}f(u)du[/imath]
Giờ bạn áp dụng rồi tính nốt nhé  . Chúc bạn thành công!
. Chúc bạn thành công!
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.