[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
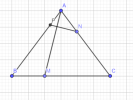
Cho [imath]\Delta ABC[/imath] đều cạnh [imath]3a[/imath]. Lấy các điểm [imath]M,N[/imath] lần lượt nằm trên cạnh [imath]BC,CA[/imath] sao cho [imath]BM=a,CN=2a[/imath]
a) Tìm giá trị của tích vô hướng [imath]\overrightarrow{AM}\cdot \overrightarrow{BC}[/imath] theo a.
b) Gọi P là điểm trên cạnh AB sao cho [imath]AM \perp PN[/imath]. Tính độ dài [imath]PN[/imath] theo [imath]a[/imath].

@Mộc Nhãn @iceghost @Cáp Ngọc Bảo Phương @chi254 @Timeless time
a) Tìm giá trị của tích vô hướng [imath]\overrightarrow{AM}\cdot \overrightarrow{BC}[/imath] theo a.
b) Gọi P là điểm trên cạnh AB sao cho [imath]AM \perp PN[/imath]. Tính độ dài [imath]PN[/imath] theo [imath]a[/imath].

@Mộc Nhãn @iceghost @Cáp Ngọc Bảo Phương @chi254 @Timeless time