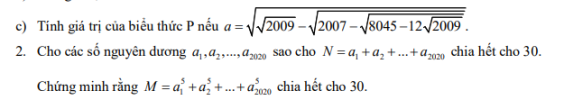Xét [imath]a_1^5 - a_1 = a_1(a_1^4 - 1) = a_1(a_1^2 - 1)(a_1^2 + 1)[/imath]
Ta có: [imath]n[/imath] chia cho 5 dư [imath]0; 1; 2;3;4[/imath]
Nên [imath]n^2[/imath] chia 5 dư [imath]0;1; 4[/imath]
Vậy [imath]a_1(a_1^2 - 1)(a_1^2 + 1) \ \vdots \ 5[/imath]
Lại có: [imath]a_1(a_1^2 - 1) = (a_1 - 1).a_1.(a_1 + 1)[/imath] là tích 3 số tự nhiên liên tiếp nên chia hết cho 6
Vậy [imath]a_1^5 - a_1 \ \vdots \ 30[/imath]
Suy ra: [imath]a_1^5 - a_1 + a_2^5 - a_2 + a_3^5 - a_3 + .... a_{2020}^5 - a_{2020} \ \vdots \ 30[/imath]
Mà: [imath]-(a_1 + a_2 + ....+ a_{2020}) \ \vdots \ 30[/imath] . Suy ra: [imath]M \ \ vdots \ 30[/imath]
Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo thêm kiến thức tại
Tổng hợp lý thuyết ôn thi HKII lớp 9 | Tổng hợp kiến thức cơ bản toán 9
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
