[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
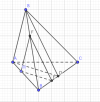
Cho tứ diện [imath]S.ABC[/imath] có 2 mặt [imath](ABC)[/imath] và [imath](SBC)[/imath] là hai tam giác đều cạnh [imath]a[/imath], [imath]SA= \frac{a\sqrt{3}}{2}[/imath]. [imath]M[/imath] là điểm trên [imath]AB[/imath] sao cho [imath]AM=b[/imath] (0<b<a). [imath](P)[/imath] là mặt phẳng qua [imath]M[/imath] và vuông góc với [imath]BC[/imath]. Thiết diện của [imath](P)[/imath] và tứ diện [imath]S.ABC[/imath] có diện tích bằng?

Em còn câu này k lm đc, mng giúp e với ạ

Em còn câu này k lm đc, mng giúp e với ạ